Lektsii_Rubleva_1 / Гл 09 Ряд та _нтеграл Фур'є / Пар 9-4 Теореми Фейєра та Вейєрштрасса

3

Глава 9

Ряд та інтеграл Фур’є

4. Теореми Фейєра та Вейєрштрасса

Нехай часткова сума РФ функції , що обчислена в точці . Покладемо

. (1)

Теорема 1.	(Ядро Фейєра)
	Якщо , то
	,	(2)
	де
	.	(3)

Доведення. Безпосередньо з теореми Діріхле ми одержимо формулу (2). Залишається довести рівність (3). Підставимо формулу ядра Діріхле і одержимо:

, що й треба було довести.

Теорема доведена.

Права частина рівності (2) називається інтегралом Фейєра, а функція - ядром Фейєра. Головна відміна цього ядра від визначеного раніше ядра Діріхле в тому, що воно невід’ємне.

Покладемо в рівності (2) , тоді одержимо:

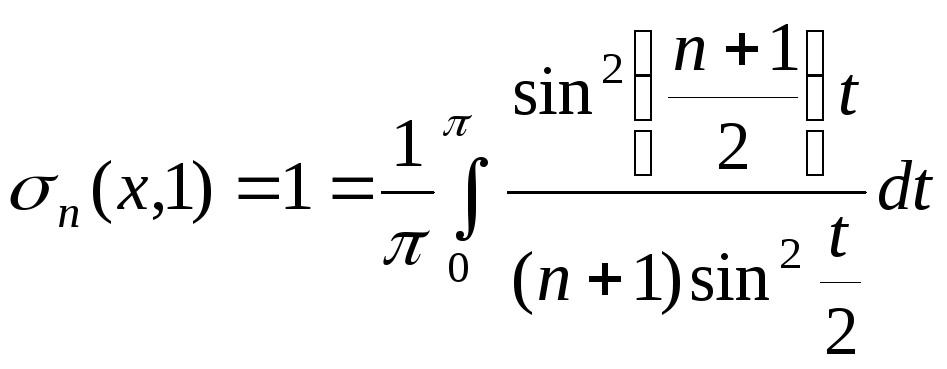. (4)

Позначимо через клас усіх - періодичних неперервних на функцій.

Теорема 2.	(Фейєра)
	Якщо , то на .

Доведення. З теореми 1 та рівності (4) ми маємо:

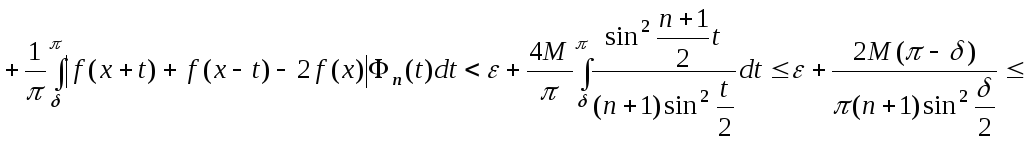
. Оскільки , то - рівномірно неперервна на : : . Нехай 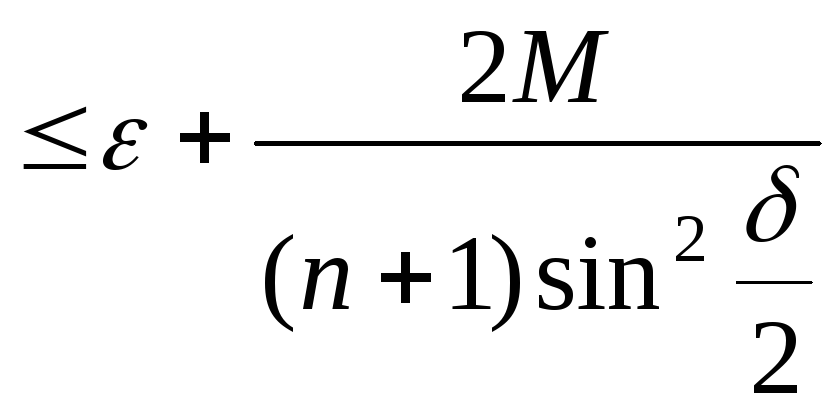. Виберемо : , тоді .

Теорема доведена.

Теорема 3.	(Вейєрштрасса про наближення неперервних функцій тригонометричними поліномами)
	Якщо , то - тригонометричний многочлен такий, що .

Доведення. Покладемо в теоремі 2 з достатньо великим .

Теорема доведена.

Теорема 4.	(Вейєрштрасса про наближення неперервних функцій поліномами)
	Якщо , то - алгебраїчний многочлен такий, що .

Доведення. Визначимо функцію за таких умов:

1) ;

2) ;

3) .

З теореми 3 - тригонометричний многочлен такий, що . Розвинемо в степеневий ряд функцію . Він має нескінченний радіус збіжності, що слідує з властивостей рядів Тейлора для синусів та косинусів. На сегменті цей степеневий ряд збігається рівномірно, тому :

. Отже . Позначимо

, а також врахуємо, що дістанемо остаточну оцінку .

Теорема доведена.

Теорема 5.	(РФ для неперервної функції)
	Тригонометричний ряд є рядом Фур’є тоді і тільки тоді, коли він рівномірно підсумовується методом середніх арифметичних, тобто .

Доведення. Необхідність безпосередньо слідує з теореми Фейєра.

Достатність. Нехай , , . Тоді маємо: .

Теорема доведена.

Теорема 5.	(РФ для інтегрованої функції)
	Нехай . Якщо існує , то РФ функції підсумовується у точці методом середніх арифметичних до числа .

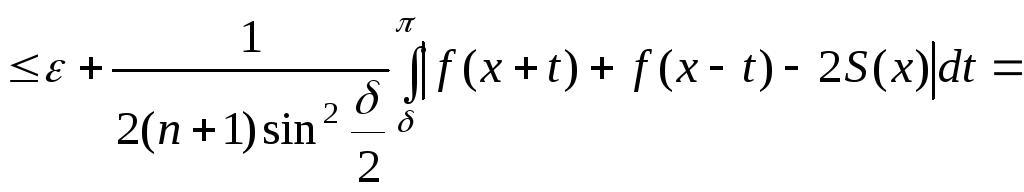
Доведення. : . Далі аналогічно доведенню теоремі Фейєра: і тепер виберемо : , і далі все доведено.

Теорема доведено.
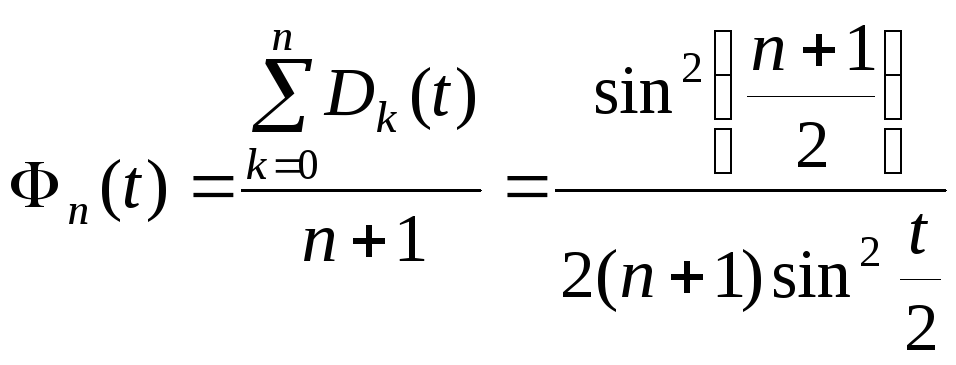