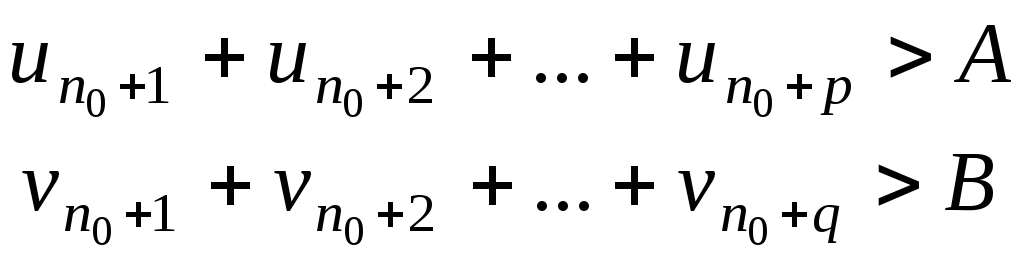Lektsii_Rubleva / Лекции Рублева-1 / Гл 06 Ряди / Пар 6-4 Теорема Р_мана та _нше

2

Глава 6

Ряди

6.4. Теорема Рімана та інші властивості рядів

Якщо відображення - бієкція, то ряд називається перестановкою ряду .

Теорема 1.	(Збіжність перестановки ряду)
	Якщо ряд збігається абсолютно та має суму , то будь-яка його перестановка також збігається та має ту ж саму суму .

Доведення. Нехай - часткові суми перестановки ряду, а , тоді послідовність - монотонно зростає та обмежена числом , а тому ця послідовність збіжна, з чого слідує абсолютна збіжність будь-якої перестановки, а тому і проста її збіжність.

З критерію Коші маємо: :

. (1)

Нехай - найбільший з індексів, який мають числа , коли вони є членами перестановки . Зрозуміло, що . Розглянемо довільне , тоді в різниці , члени ряду з номерами від до скорочуються, і залишаються лише члени з номерами, більшими за . Внаслідок (1) , а тому , що й треба було довести.

Теорема доведена.

Нехай ряд містить нескінченну кількість як додатних, так і від’ємних членів, позначимо послідовно через - додатні, а через - від’ємні члени цього ряду. Таким чином можна розглянути ряди з додатними членами та .

Теорема 2.	(Про додатну та від’ємну частини ряду)
	Якщо ряд збігається абсолютно, то також збігаються одночасно і ряди , . Якщо ж ряд збігається умовно, то обидва ряди , одночасно розбігаються.

Доведення. Нехай ряд збігається абсолютно, позначимо , тоді послідовності та монотонно зростають та обмежені числом , а тому вони збіжні, що означає збіжність рядів , .

Нехай тепер ряд збігається умовно. Якби збігалися обидва ряди , , то з рівності слідує абсолютна збіжність ряду , що суперечить умові. Якщо ж збігається рівно один з двох рядів, то з рівності , де ми маємо рівність між двома збіжними та однією розбіжною послідовностями, що неможливо. Тому обидва ряди є розбіжними.

Теорема доведена.

Наслідок.	(Необмеженість додатної та від’ємної частини ряду)
	Якщо ряд збігається умовно, то :
		(2)

Доведення наслідку слідує з того, що треба записати заперечення критерію Коші. З теореми 2 слідує, що послідовності часткових сум рядів та необмежені, з чого все й слідує.

Теорема 3.	(Рімана)
	Якщо ряд збігається умовно, то існує така перестановка цього ряду , яка збігається до .

Доведення. Розглянемо випадок , інші випадки розглядаються аналогічно. Як і раніше розглянемо додатну та від’ємну частини ряду через та . З попереднього наслідку маємо:

: та .

Аналогічно : та .

Продовжимо цей процес: : та .

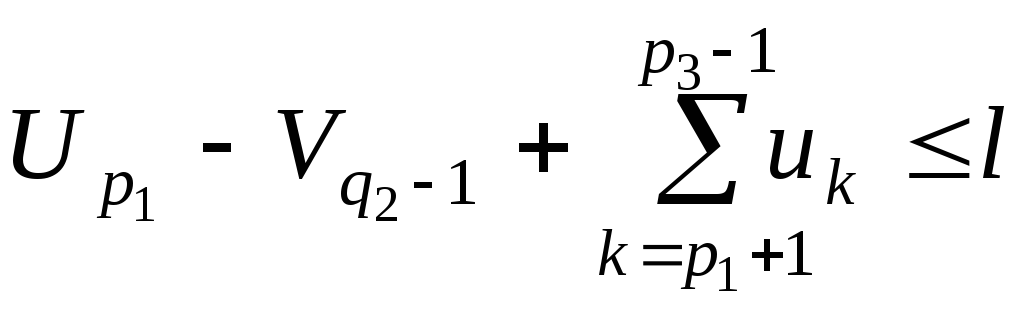Тепер знову знайдемо і т.д. ми одержали перестановку, при якій відбувається коливання часткових сум перестановки навколо числа , при цьому різниця на кожному кроці не перевищує відповідного значення чи , але з умовної збіжності ряду слідує, що загальний член цього ряду прямує до нуля, а тому прямують до нуля також послідовності та , з чого слідує, що різниця між частковою сумою перестановки та числом прямує до нуля, що й означає збіжність цієї перестановки до .

Теорема доведена.