Lektsii_Rubleva / Лекции Рублева-1 / Гл 11 Вим_рн_ функц_ї _нтеграл Лебега / Пар 11-6 _нтеграл Лебега для необмежених додатних ВФ

5

Глава 11

Вимірні функції. Інтеграл Лебега

6. Інтеграл Лебега від необмежених невід’ємних ВФ

Нехай як і раніше A - простір з скінченою мірою, функція - ВФ а також майже всюди скінчена, а також на . Позначимо через зрізку функції , що визначається рівністю: . Вимірність цієї функції очевидна, оскільки вона слідує з рівності: .

Лема 1.	(Міра точок необмеженості функції)
	Для функції, що визначена вище має місце рівність: .

Доведення. , а тому з неперервності зверху маємо: , оскільки за умовою функція майже всюди скінчена.

Лема доведена.

Оскільки усі зрізки функції - обмежені ВФ, а тому вони інтегровані за Лебегом. З того, що слідує, що , а тому існує скінчена чи нескінченна границя

. (1)

Якщо границя (1) скінчена, то функція називається інтегрованою за Лебегом, або сумовною, а її інтеграл Лебега визначається рівністю: . Якщо ж границя (1) нескінченна, то за означенням покладемо: .

Якщо - обмежена ВФ, то при достатньо великих , а тому інтеграл для обмеженої ВФ дає за обома значеннями ті ж самі значення.

Лема 2.	(достатня ознака існування ІЛ для необмежених функцій)
	Нехай - невід’ємні ВФ і на , та функція - сумовна на . Тоді функція також сумовна на та справджується нерівність:
	.	(2)

Доведення. З умови слідує, що . Згідно теореми про ІЛ для нерівних функцій та визначенню ІЛ для необмеженої функції маємо:

. (3)

з цієї нерівності слідує скінченність границі , а тому й сумовність . Переходячи до границі при в нерівності (3), одержимо потрібну нерівність (2).

Лема доведена.

Якщо - інтегрована на функція, - вимірна множина. Тоді - ВФ, при цьому , а тому з леми 2 функція також сумовна, а тому природнім стає наступне означення.

Якщо множина - вимірна, а функція - сумовна на , то функція називається сумовною на множині , а її інтеграл по цій множині визначається рівністю: . Зрозуміло, що якщо функція сумовна на усьому просторі , то вона також сумовна на будь-якій вимірній підмножині цього простору.

Теорема 1.	(Лінійність ІЛ для необмежених функцій)
	Якщо - невід’ємні сумовні функції, то функція також сумовна і .

Доведення. По черзі перевіримо адитивність та однорідність інтегралу Лебега.

, а тому можемо записати нерівності:

, а тому функція сумовна. Граничним переходом одержимо, що . З іншого боку, , а тому . Знову робимо граничний перехід і одержимо: . Ці дві нерівності й доводять адитивність ІЛ.

Тепер однорідність. При - очевидно. Нехай тепер . Тоді , а тому . Звідси слідує сумовність функції . Після граничного переходу ми маємо першу нерівність:

. А з того, що , то з сумованості вище доведеної функції одержимо, що , а після граничного переходу одержимо другу нерівність: , з якої слідує рівність при . Нехай . З того,

що , то функція - сумовна. Оскільки , то з доведеного вище маємо: , звідки й слідує потрібна рівність .

Теорема доведена.

Нехай деяка фіксована невід’ємна сумовна функція на . Розглянемо функцію для довільної вимірної множини .

Теорема 2.	(Абсолютна неперервність ІЛ як функції множин)
	Якщо - невід’ємна сумовна функція, то функція множин абсолютно неперервна відносно міри , тобто : A .

Доведення. З визначення ІЛ для необмеженої невід’ємної ВФ слідує, що : . Якщо покласти , то для будь-якої ВМ , що задовольняє умову , одержимо:

.

Теорема доведена.

Теорема 3.	(Злічена адитивність ІЛ як функції множин)
	Якщо - невід’ємна сумовна функція, то функція множин злічено адитивна, тобто якщо , A, то .

Доведення. Досить легко показати скінчену адитивність функції : якщо , то 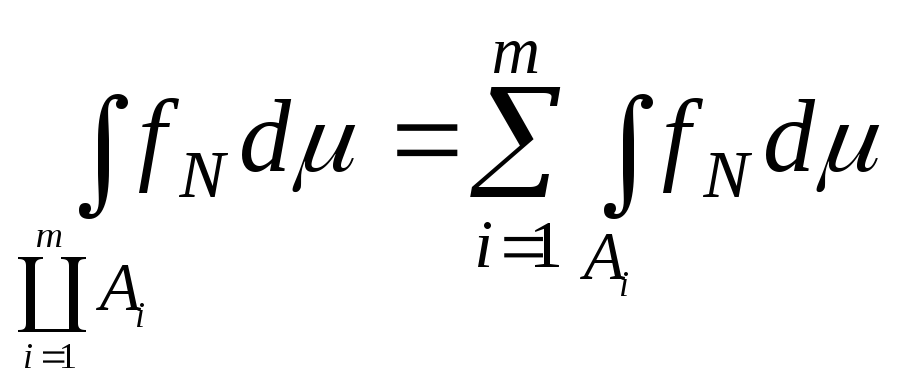. Далі граничним переходом отримаємо скінчену адитивність функції . З попередньої теореми : . Із зліченої адитивності міри , а тому : . А далі із скінченої адитивності маємо: , де останній доданок не перевищує . А тому .

Теорема доведена.

Нехай тепер функція вимірна майже всюди скінчена. Розглянемо від’ємну та додатну частини цієї функції: , які мають властивості – вони невід’ємні, також майже всюди скінченні та вимірні. Крім того . Для обох цих функцій визначено поняття інтегрованості за Лебегом, як для невід’ємних функцій, а тому природно дати таке визначення.

Функція називається сумованою (інтегрованою за Лебегом) на , якщо сумовна обидві функції . При цьому інтеграл Лебега від функції визначається рівністю: .

Теорема 4.	(Модуль ІЛ та ІЛ від модуля довільної ВФ)
	Для сумованості ВФ необхідно й достатньо, щоб була сумована функція . При цьому їх інтеграли пов’язані нерівністю: .

Доведення. Необхідність. Нехай - сумовна, тоді також сумовані функції , але тоді з лінійності ІЛ для невід’ємних функцій сумована й функція . При цьому: .

Достатність. Нехай - сумована, тоді , а тому сумовані також і функції , а тому сумована й функція .

Далі маємо: .

Теорема доведена.

Наслідок.	(Достатня ознака існування ІЛ довільної ВФ)
	Якщо ВФ та , де - сумована функція, то також сумована функція.

Якщо - сумовна функція, - ВМ, тоді функція - також сумовна, оскільки . А тому природнім виглядає наступне визначення.

Якщо множина - вимірна, та функція - сумовна на , то функція називається сумовною на множині та її інтеграл визначається рівністю:

.

Теорема 5.	(Лінійність ІЛ для довільної необмеженої ВФ)
	Якщо - сумовні функції, то функція також сумовна і .

Доведення. З простої нерівності слідує умовність функції .

Тепер адитивність. Якщо - сумовні, то оскільки , та . Прирівняємо останні два вирази і одержимо:

.

Усі функції невід’ємні. А тому для них можна скористатися властивістю лінійності:

, , що й доводить те що потрібно.

Нехай - сумовна функція, . Тоді , , а тому . Звідки і маємо однорідність для додатних . Тепер перевіримо для від’ємних , для цього достатньо перевірити для . Оскільки

Нехай задана деяка обмежена ВФ , розглянемо функцію множин, що для будь-якої вимірної множини задається рівністю:

. (4)

Теорема 6.	(Злічена адитивність ІЛ для необмежених функцій)
	Функція множин злічено адитивна, тобто, якщо A, то

Теорема 7.	(Абсолютна неперервність ІЛ для необмеженої функції)
	Якщо - сумовна функція, то функція множин , що визначається формулою (4) абсолютно неперервна відносно міри .