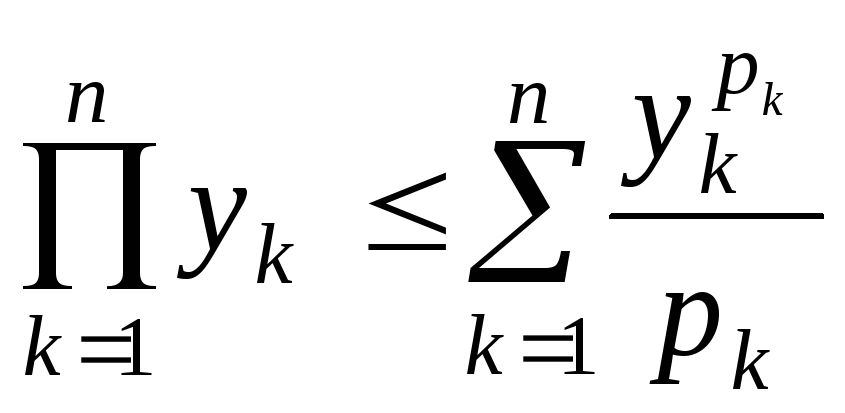Lektsii_Rubleva / Лекции Рублева-1 / Гл 02 Пох_дна / Пар 2-08 Опукл_ функц_ї
.doc
Глава 2
Похідна
8. Опуклі функції, класичні нерівності
Нехай
![]() ,
,
![]() - дві точки на декартовій площині,
відрізком
- дві точки на декартовій площині,
відрізком
![]() називається множина точок
називається множина точок
![]() .
.
Множина
![]() називається опуклою,
якщо
називається опуклою,
якщо
![]() .
.
Нехай
![]() - графік функції
- графік функції
![]() ,
надграфіком
(підграфіком)
цієї функції називається множина
,
надграфіком
(підграфіком)
цієї функції називається множина
![]()
![]() При цьому будемо казати, що точка
При цьому будемо казати, що точка
![]() лежить
вище
(нижче)
графіка, якщо вона належить надграфіку
(підграфіку) цієї функції.
лежить
вище
(нижче)
графіка, якщо вона належить надграфіку
(підграфіку) цієї функції.
Функція
![]() називається опуклою
(угнутою),
якщо її над графік (під графік) є опуклою
множиною.
називається опуклою
(угнутою),
якщо її над графік (під графік) є опуклою
множиною.
Легко з означення опуклої множини зрозуміти, що мова про опуклу (угнуту) функцію має сенс, якщо вона визначена на зв’язній множині, тобто в якості області визначення в цьому розділі опуклих функцій ми будемо розглядати лише сегменти, інтервали та півінтервали, або будь-які промені.
Нагадаємо,
що число
![]() визначає кутовий
коефіцієнтом прямої,
що проходить через точки
визначає кутовий
коефіцієнтом прямої,
що проходить через точки
![]() та
та
![]() .
.
|
Лема 1. |
(Про три точки) |
|
|
|
Нехай на
декартовій площині задано три точки
|
|
|
1) |
|
|
|
2) |
|
|
|
3) |
|
|
|
4) |
|
|
|
Доведення леми. Розглянемо
як на малюнку точки
Лему доведено.
|
|
|
|
Рис. 1 |
||
|
Теорема 1. |
(Односторонні похідні опуклої функції) |
|
|
Нехай
функція
|
Доведення
теореми. Нехай
![]() - довільні значення, що задовольняють
умові:
- довільні значення, що задовольняють
умові:
![]() .
Розглянемо три точки
.
Розглянемо три точки
![]() ,
,
![]() ,
,
![]() .
Згідно з означенням опуклої функції
.
Згідно з означенням опуклої функції
![]() лежить нижче прямої
лежить нижче прямої
![]() .
За лемою 1 ми маємо:
.
За лемою 1 ми маємо:
![]()
![]()
![]()
![]() функції
функції
![]()
![]() ,
,
![]() і
і
![]()
![]() ,
,
![]() - неспадні. Тому існують
- неспадні. Тому існують
![]() ,
,
![]() .
Внаслідок довільності
.
Внаслідок довільності
![]() ліва та права похідні існують в кожній
точці
ліва та права похідні існують в кожній
точці
![]() .
Розглянемо нерівність:
.
Розглянемо нерівність:
![]() .
Зробимо граничний перехід при
.
Зробимо граничний перехід при
![]()
![]() .
Далі робимо граничний перехід при
.
Далі робимо граничний перехід при
![]() ,
тоді одержимо
,
тоді одержимо
![]()
![]() - неспадна, аналогічно для
- неспадна, аналогічно для
![]() .
.
Теорему доведено.
|
Наслідок 1. |
(Неперервність опуклої функції) |
|
|
Кожна
опукла функція
|
Доведення. З того, що існує ліва похідна в кожній точці слідує, що функція неперервна зліва, аналогічно – вона неперервна справа. А це і означає неперервність функції в кожній точці.
Наслідок доведено.
|
Наслідок 2. |
Похідна опуклої функції) |
|
|
Якщо
|
Доведення.
Розглянемо множини точок
![]() ,
в якій розривні ліва та права похідні.
З властивостей монотонних функцій ці
множини не більш ніж злічені. Розглянемо
множину
,
в якій розривні ліва та права похідні.
З властивостей монотонних функцій ці
множини не більш ніж злічені. Розглянемо
множину
![]() ,
вона також не більш ніж злічена. В усіх
інших точках права та ліва похідні
неперервні. Покажемо таким чином, що в
цих точках права та ліва похідні
співпадають.
,
вона також не більш ніж злічена. В усіх
інших точках права та ліва похідні
неперервні. Покажемо таким чином, що в
цих точках права та ліва похідні
співпадають.
Від
супротивного. Припустимо, що вони в
точці
![]() неперервні та мають різні значення.
Припустимо, що
неперервні та мають різні значення.
Припустимо, що
![]() .
Без обмежень загальності можемо вважати,
що
.
Без обмежень загальності можемо вважати,
що
![]() ,
а інакше можна розглянути функцію
,
а інакше можна розглянути функцію
![]() ,
для якої це має місце, а зайвий доданок
не впливає на диференційованість функції
,
для якої це має місце, а зайвий доданок
не впливає на диференційованість функції
![]() .
Тобто, нехай
.
Тобто, нехай
![]() .
Але внаслідок стійкості нерівності для
неперервної функції знак кожної похідної
зберігається в деякому околі точки
.
Але внаслідок стійкості нерівності для
неперервної функції знак кожної похідної
зберігається в деякому околі точки
![]() .
Виберемо найменший з цих околів
.
Виберемо найменший з цих околів
![]() ,
в якому функції
,
в якому функції
![]() зберігають знак. Виберемо точки
зберігають знак. Виберемо точки
![]() ,
для яких
,
для яких
![]() та
та
![]() .
Але тоді з узагальненої теореми Лагранжа
.
Але тоді з узагальненої теореми Лагранжа
![]() (для правої похідної), та
(для правої похідної), та
![]() (для лівої похідної). Одержана суперечність
доводить потрібне. Тепер ми бачимо, що
вони співпадають в точках неперервності,
а тому й сама похідна співпадає з цими
значеннями, а тому також є неперервною
в точці
(для лівої похідної). Одержана суперечність
доводить потрібне. Тепер ми бачимо, що
вони співпадають в точках неперервності,
а тому й сама похідна співпадає з цими
значеннями, а тому також є неперервною
в точці
![]() ,
а тому й на усій множині
,
а тому й на усій множині
![]() .
.
Наслідок доведено.
|
Теорема 2. |
(Критерій опуклості функції) |
|
|
Для того,
щоб функція
|
Доведення теореми. Необхідність безпосередньо слідує з теореми 2.
Для достатності доведемо два допоміжні твердження.
|
Лема 2. |
(Теорема Ферма для лівої похідної) |
|
|
Якщо функція
|
Доведення
леми. З того,
що
![]() - точка найбільшого значення
- точка найбільшого значення
![]()
![]()
![]()
![]() .
.
Аналогічно для найменшого значення.
Лему доведено.
|
Лема 3. |
(Теорема Лагранжа для лівої похідної) |
|
|
Якщо функція
|
Доведення
леми. Покладемо
![]() і розглянемо функцію
і розглянемо функцію
![]() ,
,
![]() .
.
![]()
![]() набуває найбільшого та найменшого
значення в деяких точках
набуває найбільшого та найменшого
значення в деяких точках
![]() та
та
![]() .
Оскільки
.
Оскільки
![]() (їх можна вибрати на цьому півінтервалі).
Тоді за попередньою лемою
(їх можна вибрати на цьому півінтервалі).
Тоді за попередньою лемою
![]() ,
,
![]()
![]()
![]() .
.
Лему доведено.
Нехай
![]() ,
,
![]() лежать вище графіка функції
лежать вище графіка функції
![]() ,
а
,
а
![]() .
Покажемо, що
.
Покажемо, що
![]() (що буде означати опуклість функції
(що буде означати опуклість функції
![]() ).
За теоремою Лагранжа для лівої похідної:
).
За теоремою Лагранжа для лівої похідної:
![]() :
:
![]() ,
аналогічно
,
аналогічно
![]() :
:
![]() .
Оскільки
.
Оскільки
![]() і
і
![]() неспадна, то
неспадна, то
![]() за лемою про три точки
за лемою про три точки
![]() .
.
Лему доведено.
|
Наслідок 1. |
(Критерій опуклості функції через праву похідну) |
|
|
Для
того, щоб функція
|
|
Наслідок 2. |
(Критерій опуклості диференційованої функції) |
|
|
Якщо
функція
|
|
Наслідок 3. |
(Критерій опуклості двічі диференційованої функції) |
|
|
Якщо
функція
|
|
Теорема 3. |
(Ієнсена) |
|
|
|
Нехай
функція
|
|
|
|
|
(1) |
Доведення
теореми. Для
![]() маємо: покладемо
маємо: покладемо
![]() .
Розглянемо точки
.
Розглянемо точки
![]() ,
,
![]() .
Тоді точка
.
Тоді точка
![]() ,
де
,
де
![]() ,
,
![]() належить відрізку
належить відрізку
![]() ,
тому з означення опуклої функції
,
тому з означення опуклої функції
![]() ,
тобто
,
тобто
 - доведено для
- доведено для
![]() .
.
Нехай
(1)
має місце для
![]() ,
доведемо з цього його істинність для
,
доведемо з цього його істинність для
![]() .
.
Позначимо
 .
Очевидно, що
.
Очевидно, що
![]() .
Використаємо нерівність (1)
для
.
Використаємо нерівність (1)
для
![]() (
вона вже доведена).
(
вона вже доведена).

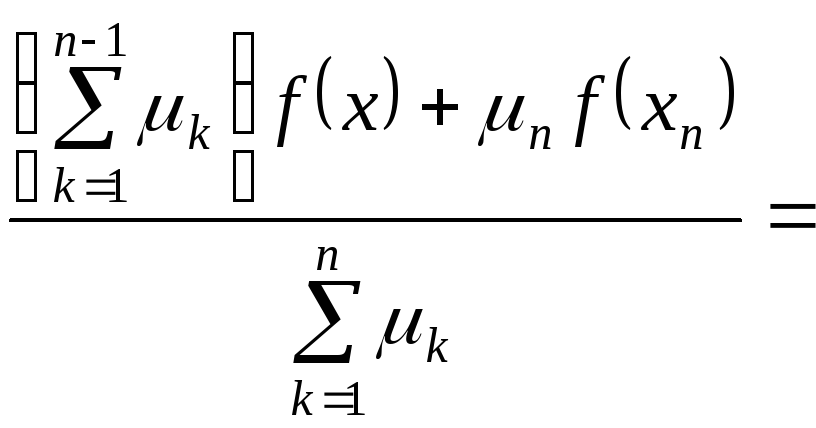
=
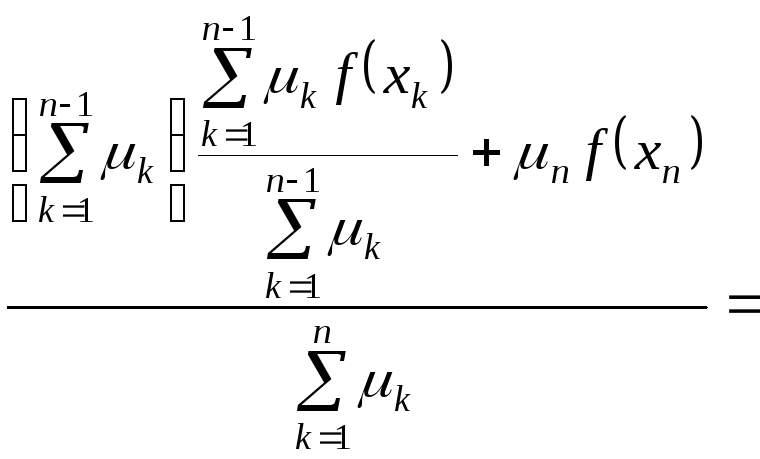
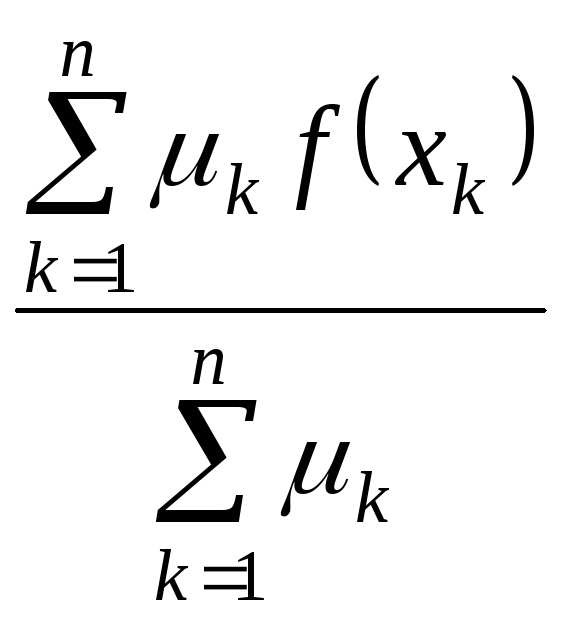 .
.
Теорему доведено.
|
Наслідок. |
(Нерівність між середніми) |
|
|
Якщо
|
Доведення.
Розглянемо
на
![]() функцію
функцію
![]() .
.
![]() ,
,
![]()
![]() опукла
опукла
![]() поклавши в нерівності (1)
поклавши в нерівності (1)
![]()
![]()
 .
.
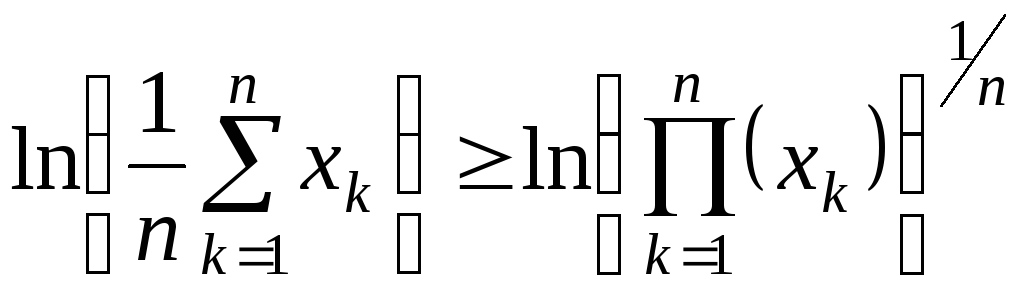
![]()
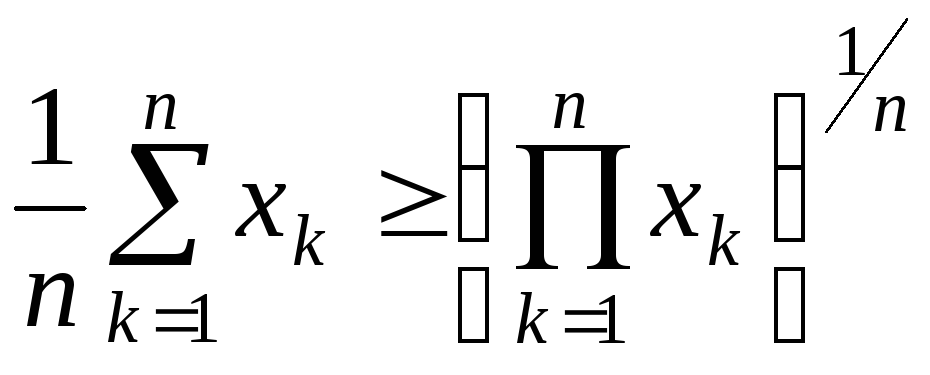 .
.
Наслідок доведено.
|
Теорема 4. |
(Еквівалентний критерій опуклості функції)) |
|
|
|
Функція
|
|
|
|
|
(2) |
Необхідність
слідує з нерівності Ієнсена, якщо
покласти
![]() ,
,
![]() ,
,
![]() .
.
Достатність.
Нехай
![]() .
Тоді
.
Тоді
![]()
![]() .
Покладемо
.
Покладемо
![]() ,
тоді
,
тоді
![]() ,
,
![]()
![]()
![]() ,
,
![]()
![]()
![]()
![]()
![]() - опукла.
- опукла.
Теорему доведено.
З останньої теореми можна дати еквівалентне означення опуклій функції.
Функція
![]() називається опуклою
(строго
опуклою),
якщо
називається опуклою
(строго
опуклою),
якщо
![]() ,
,
![]() виконується нерівність
виконується нерівність
![]() .
.
Функція
![]() називається угнутою
(строго
угнутою),
якщо функція
називається угнутою
(строго
угнутою),
якщо функція
![]() опукла (строго опукла).
опукла (строго опукла).
|
Теорема 5. |
(Лінійність опуклості) |
|
|
Нехай
функції
|
|
|
Якщо при
цьому хоч одна з функцій
|
Доведення очевидно проводиться методом математичної індукції.
|
Теорема 6. |
(Нерівність Юнга) |
|
|
|
Нехай
|
|
|
|
|
(3) |
Доведення.
![]() ,
,
![]()
![]() опукла. Покладемо в нерівності Ієнсена:
опукла. Покладемо в нерівності Ієнсена:
![]() ,
,
![]()
![]()
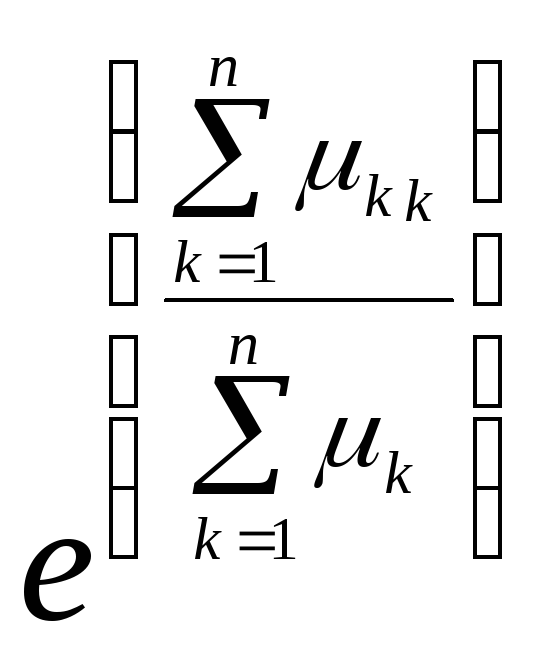
![]()
![]()
![]()
![]() .
.
Теорему доведено.
|
Теорема 7. |
(Нерівність Гельдера) |
|
|
|
Нехай
|
|
|
|
|
(4) |

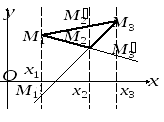
 неперервна.
неперервна.
 .
.