Lektsii_Rubleva / Лекции Рублева-1 / Гл 09 Ряд та _нтеграл Фур'є / Пар 9-8 РФ в г_льбертових просторах

6

Глава 9

Ряд та інтеграл Фур’є

8. Ряди Фур’є в гільбертових просторах

Векторний простір називається евклідовим простором (ЕП) (над полем ), якщо в ньому визначена функція скалярний добуток (СД) 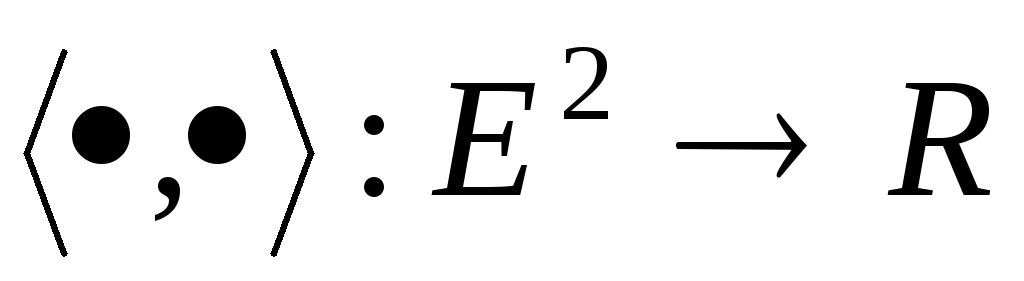, який задовольняє наступним аксіомам:

1. , ;

2. ;

3. ;

4. .

Лема 1.	(Визначення норми в ЕП)
	В ЕП можна визначити норму за формулою.
		(1)

При цьому норма називається узгодженою із СД. В подальшому будемо вважати, що якщо заданий ЕП, то норма в ньому узгоджена із СД.

Лема 2.	(Неперервність СД)
	СД в ЕП є неперервною на функцією.

Обидві леми були доведені в темі ФБЗ.

Вектори називаються ортогональними, якщо . Сім’я векторів називається ортогональною, якщо , . Сім’я векторів називається ортонормованою (ОНСВ), якщо вона ортогональна і при цьому .

Теорема 1.	(Ортогональність основної тригонометричної системи)
	Нехай - інтервал довжини і . Тоді сім’я векторів ортогональна в евклідовому просторі .

Доведення. Нагадаємо, що скалярний добуток в просторі визначається за формулою:

(2)

Нехай , тоді .

Теорема доведена.

Наслідок 1.	(Ортонормованість основної тригонометричної системи)
	Сім’я векторів ОНСВ в просторі .

Для доведення достатньо обчислити норму елемента:

.

Наслідок 2.	(Ортонормована тригонометрична система)
	Нехай , тоді сім’я векторів , є ОНСВ в просторі .

Гільбертовим простором (ГП) називається ЕП, що є повним у нормі, що узгоджена із скалярним добутком.

Теорема 2.	(Фішера-Рісса про повноту простору)
	Простір , де - обмежений проміжок дійсної осі, є гільбертовим.

Без доведення.

Нехай - ГП. Ряд в цьому просторі називається збіжним (збіжним до елемента ), якщо збігається послідовність (якщо послідовність , тобто при ), де - послідовність часткових сум.

Теорема 3.	(Критерій збіжності ортогонального ряду)
	Ортогональний ряд (тобто ряд, члени якого утворюють ортогональну систему) елементів ГП збігається тоді і тільки тоді, коли:
	.	(3)

Доведення. Оскільки , а далі твердження слідує з повноти просторів та .

Теорема доведена.

Нехай - ЕП, ряд елементів цього простору називається безумовно збіжним, якщо для будь-якої бієкції збігається ряд .

Теорема 4.	(Критерій безумовної збіжності ортогонального ряду)
	Ортогональний ряд елементів ГП безумовно збігається тоді і тільки тоді, коли виконується умова (3).

Доведення. Оскільки для будь-якої бієкції ряд є ортогональним і і все слідує з теореми 3.

Теорема доведена.

Нехай зафіксовано ОНСВ у ГП .

Теорема 5.	(Коефіцієнти збіжного ряду)
	Якщо ряд збігається і , то:
	.	(4)

Доведення. Внаслідок неперервності СД маємо: .

Теорема доведена.

Ряд , що побудований для заданої ОНСВ ГП , коефіцієнти якого обчислюються за формулами (4) називається рядом Фур’є елемента (РФ) по ОНСВ .

З теореми 5 слідує, що будь-який збіжний в ГП ряд по ОНСВ є РФ своєї суми, але це не виключає, що він є РФ іншого елемента та не збігається до .

Теорема 6.	(Нерівність Бесселя)
	Нехай ОНСВ у ГП . Тоді справджується нерівність Бесселя:
	.	(5)

Доведення. Нехай . Тоді згідно з властивостями СД та нерівності Шварца маємо: , яке виконується , що і є рівносильним нерівності Бесселя (5).

Теорема доведена.

Теорема 7.	(Про збіжність РФ)
	Кожен РФ по ОНСВ збігається у ГП (але не обов’язково до відповідного елемента).

Доведення слідує з теореми 3 та нерівності Бесселя.

Теорема 8.	(Про збіжність ортогонального ряду)
	Ортогональний ряд в ГП збігається тоді і тільки тоді, коли він є РФ деякого елемента.

Доведення слідує з теорем 5 і 7.

Теорема 9.	(Фішера-Рісса про збіжність ряду)
	Нехай - ОНСВ в ГП . Якщо для послідовності збігається ряд , то існує такий елемент , що .

Доведення. З теореми 3 ряд збігається в просторі . За теоремою 5 він є РФ своєї суми.

Теорема доведена.

Теорема 10.	(Рівність Парсеваля-Стєклова)
	РФ елемента по ОНСВ у ГП збігається до вектора тоді і тільки тоді, коли справджується рівність Парсеваля-Стєклова:
	.	(6)

Доведення одержимо с тотожності:

, . (7)

Наслідок.	(Рівність Парсеваля-Стєклова для тригонометричної системи)
	Для тригонометричних РФ рівність Парсеваля-Стєклова набуває вигляду:
	,	(8)
	або ж, враховуючи показникові форму запису коефіцієнтів Фур’є, тобто , рівність набуває вигляду:
		(9)

Сім’я векторів ГП називається повною, якщо не існує ненульового вектора : .

Сім’я векторів ГП називається замкненою, якщо :

. (10)

Теорема 11.	(Зв’язок повноти та замкненості системи)
	Для ОНСВ ГП наступні умови рівносильні:
1)	Система векторів замкнена в ;
2)	Система векторів повна в ;
3)	РФ елемента має суму, яка дорівнює ;
4)	виконується рівність Парсеваля-Стєклова.

Доведення проведемо за схемою 4)3)1)2)3).

4)3) доведено в теоремі 10.

3)1) слідує з означення замкненої системи.

1)2) нехай внаслідок лінійності та неперервності СД елемент ортогональний замиканню лінійної оболонки системи векторів , яке згідно означення збігається з , отже ортогональний і собі .

2)3) , нехай РФ , а тому він є РФ елемента .

Теорема доведена.

Нехай - ГП, - множина його векторів, що задовольняє умови:

1) ;

2) , ;

тоді множина називається підпростором.

Вектор називається ортогональним підпростору , якщо , будемо це записувати .

Теорема 12.	(Ортогональність вектору підпростору)
	Нехай повна ОНСВ у ГП і . Вектор .

Доведення. Необхідність. .

Достатність. і виконується рівність: .

Теорема доведена.

Нехай - підпростір ГП . Вектор називається ортогональною проекцією елемента на , якщо .

Теорема 13.	(Про ортогональну проекцію)
	Нехай повна ОНСВ у ГП і . Тоді існує єдина ортогональна проекція вектора на підпростір і справджується формула:
	.	(11)

Доведення. Якщо виконується (11), то , а тому , що й означає ортогональність . Доведемо від супротивного, що вона єдина: і при цьому .

Теорема доведена.

Нехай - довільний ГП. Упорядкований набір векторів простору називається орієнтованим трикутником, якщо . Вектори називаються його сторонами. Трикутник називається прямокутним, якщо в нього існують дві ортогональні сторони, що називаються катетами, третя сторона називається гіпотенузою.