
Lektsii_Rubleva / Лекции Рублева-1 / Гл 01 Вступ до анал_зу - копия / Пар 1-05 П_дпосл_довност_
.doc
Глава 1
Вступ до аналізу
5. Підпослідовності
Нехай
![]() -
деяка послідовність,
-
деяка послідовність,
![]() зростаюча послідовність натуральних
чисел. Послідовність
зростаюча послідовність натуральних
чисел. Послідовність
![]() називається підпослідовністю
послідовності
називається підпослідовністю
послідовності
![]() .
.
Приклад 1. |
Для
послідовності
1)
|
Теорема 1. |
(Підпослідовності збіжної послідовності). |
|
Нехай
послідовність |
Доведення.
Нехай
![]() довільна підпослідовність послідовності
довільна підпослідовність послідовності
![]() .
За означенням границі:
.
За означенням границі:
![]()
![]()
![]()
![]()
![]() .
З того, що
.
З того, що
![]() - зростаюча послідовність натуральних
чисел, зрозуміло, що
- зростаюча послідовність натуральних
чисел, зрозуміло, що
![]()
![]()
![]()
![]()
![]() .
Поєднуючи два останні твердження, ми
одержимо, що
.
Поєднуючи два останні твердження, ми
одержимо, що
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
з чого слідує, що
,
з чого слідує, що
![]() при
при
![]() .
.
Теорема доведена.
Точка
![]() називається частковою
границею послідовності
називається частковою
границею послідовності
![]() ,
якщо існує підпослідовність
,
якщо існує підпослідовність
![]() ,
границя якої дорівнює
,
границя якої дорівнює
![]() .
.
Приклад 2. |
У
послідовності
|
Приклад 3. |
У
послідовності
|
Наслідок. |
(Множина часткових границь збіжної послідовності) |
|
Якщо
послідовність
|
Нехай
послідовність
![]() з
з
![]() обмежена, тоді
обмежена, тоді
![]() множина
множина
![]() обмежена, внаслідок повноти
обмежена, внаслідок повноти
![]() існує число
існує число
![]() .
Згідно з властивістю верхньої межі
.
Згідно з властивістю верхньої межі
![]() послідовність
послідовність
![]() монотонно незростаюча, крім того
очевидно, що вона є обмеженою, тому за
теоремою Вейєрштрасса має границю, яка
називається верхньою
границею послідовності
монотонно незростаюча, крім того
очевидно, що вона є обмеженою, тому за
теоремою Вейєрштрасса має границю, яка
називається верхньою
границею послідовності
![]() і позначається
і позначається
![]() ,
тобто
,
тобто
![]() (1)
(1)
Аналогічно визначається нижня границя послідовності:
![]() (2)
(2)
Теорема 2. |
(Критерій збіжності послідовності через верхню та нижню границі). |
|
Для
будь-якої обмеженої послідовності
|
Доведення.
З очевидної нерівності
![]()
![]() слідує бажана нерівність, якщо зробити
відповідний граничний перехід при
слідує бажана нерівність, якщо зробити
відповідний граничний перехід при
![]() .
.
Необхідність.
Нехай тепер
![]() .
Оскільки
.
Оскільки
![]()
![]() .
Далі, границя лівої та правої частини
співпадають, з чого слідує існування
границі середньої послідовності.
.
Далі, границя лівої та правої частини
співпадають, з чого слідує існування
границі середньої послідовності.
Достатність.
Нехай тепер існує
![]() .
Тоді
.
Тоді
![]()
![]()
![]()
![]() ,
тобто
,
тобто
![]()
![]()
![]()
![]()
![]() ,
але це означає, що
,
але це означає, що
![]()
![]()
![]() .
.
Теорема доведена.
Наслідок. |
(Критерій збіжності необмеженої послідовності через верхню та нижню границі). |
|
Теорема залишається чинною, якщо послідовність необмежена. |
Властивість1. |
(Перша властивість верхньої (нижньої) границі). |
|
Верхня
(нижня) границя послідовності
|
Доведення.
За побудовою, послідовність
![]() монотонно не зростає і має границею
число
монотонно не зростає і має границею
число
![]() .
Розглянемо лише варіант
.
Розглянемо лише варіант
![]() .
Інші варіанти розглядаються аналогічно.
Тоді можливі два випадки:
.
Інші варіанти розглядаються аналогічно.
Тоді можливі два випадки:
-
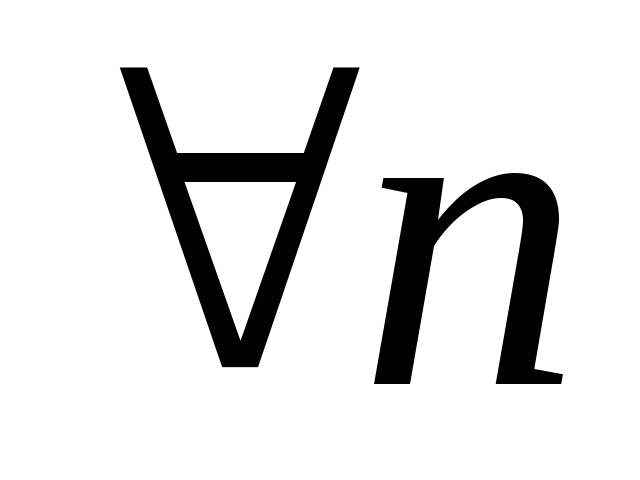
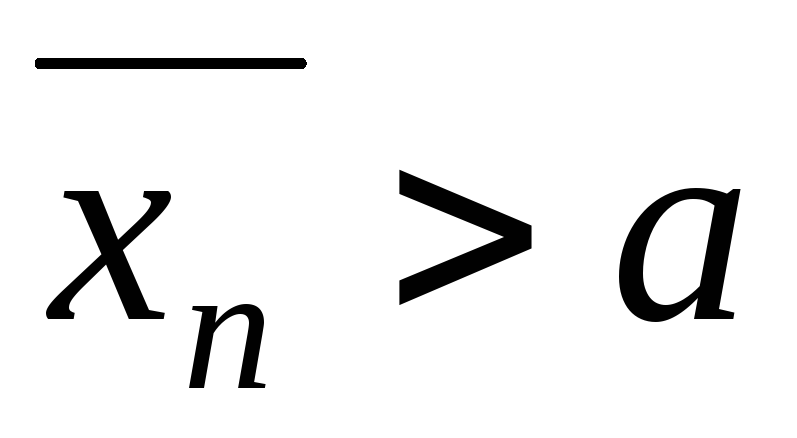 ,
тоді
,
тоді
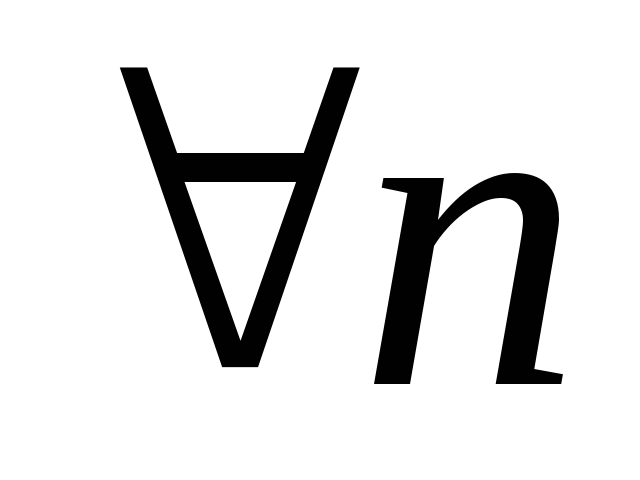
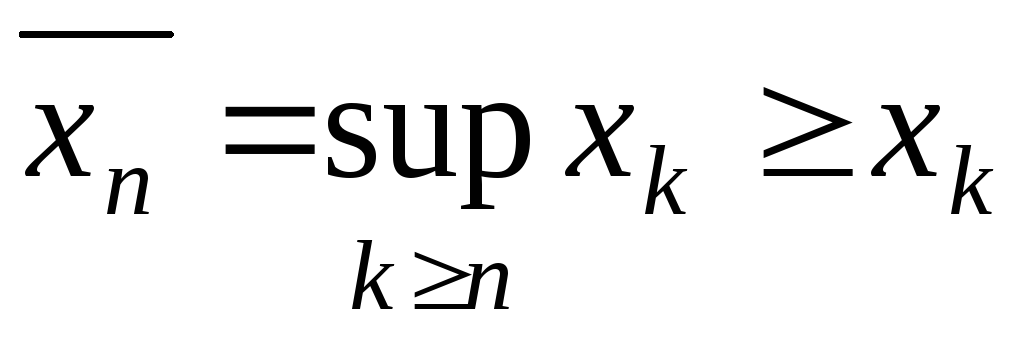
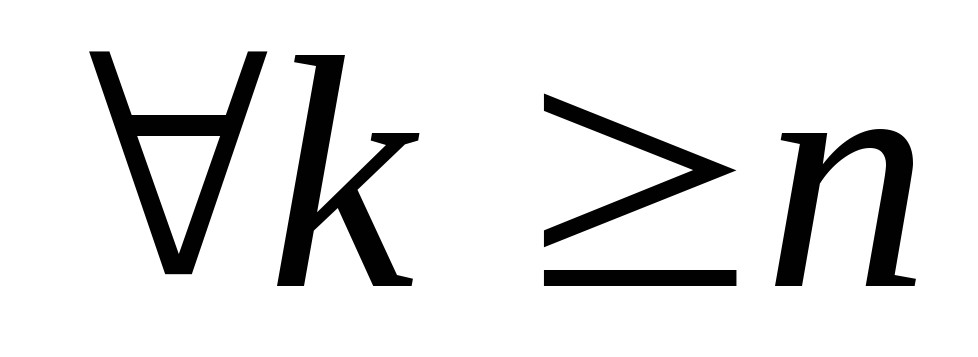

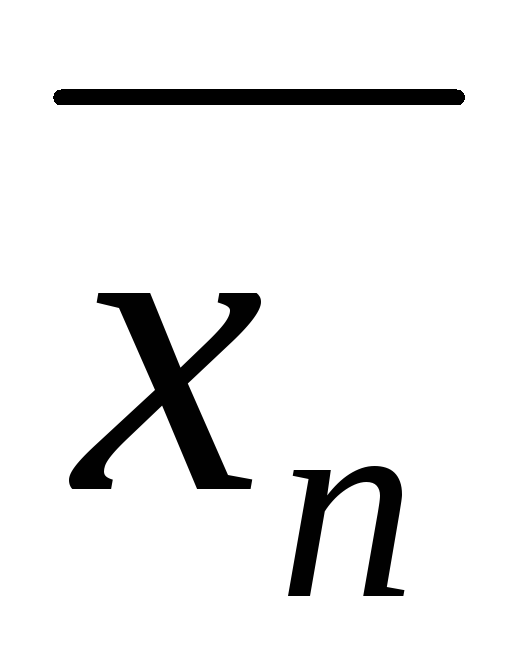 - точка дотику
- точка дотику

 в околі
в околі
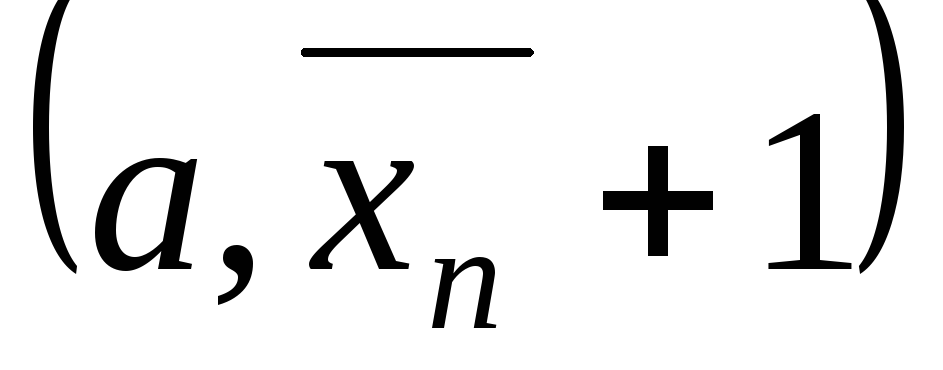 є точка з
є точка з
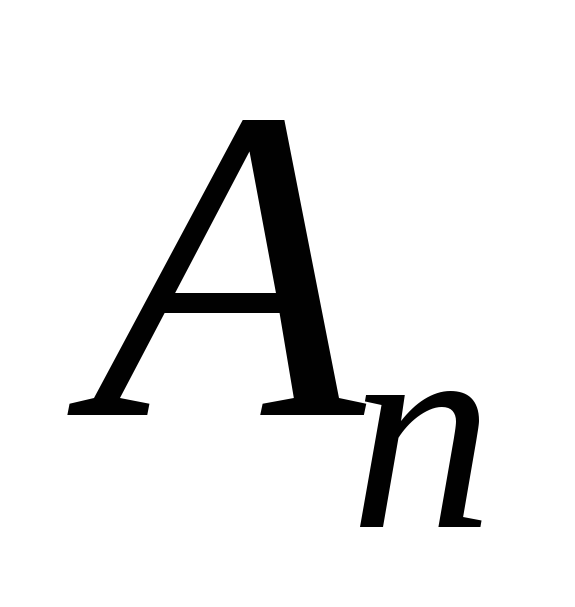 ,
але вона зліва від
,
але вона зліва від
 .
Тому підпослідовність будуємо так:
знаходимо відповідну точку для
.
Тому підпослідовність будуємо так:
знаходимо відповідну точку для
 ,
позначимо її через
,
позначимо її через
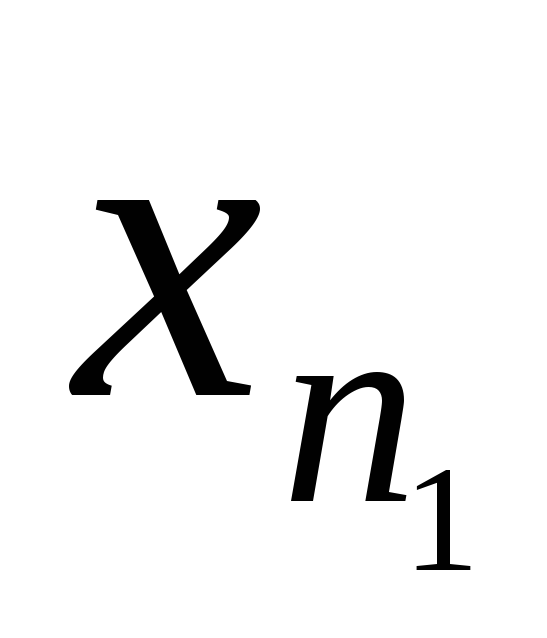 ,
далі знаходимо для
,
далі знаходимо для
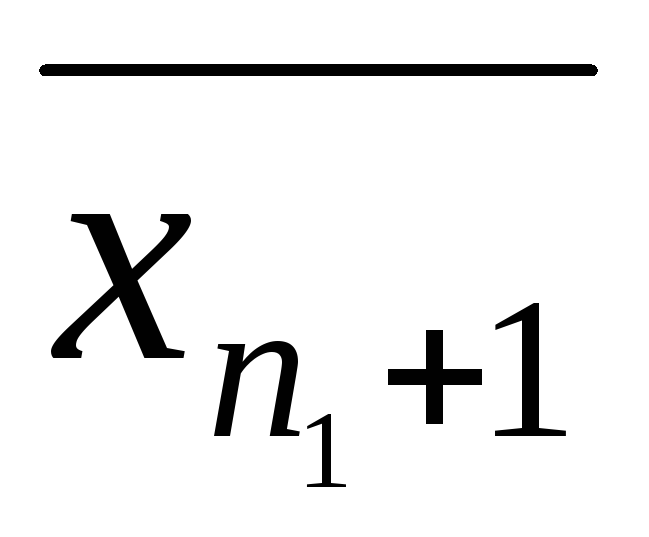 свою точку і позначаємо її
свою точку і позначаємо її
 і так далі. Для побудованої підпослідовності
виконуються нерівності:
і так далі. Для побудованої підпослідовності
виконуються нерівності:
 ,
права послідовність прямує до
,
права послідовність прямує до
 ,
з чого маємо
,
з чого маємо
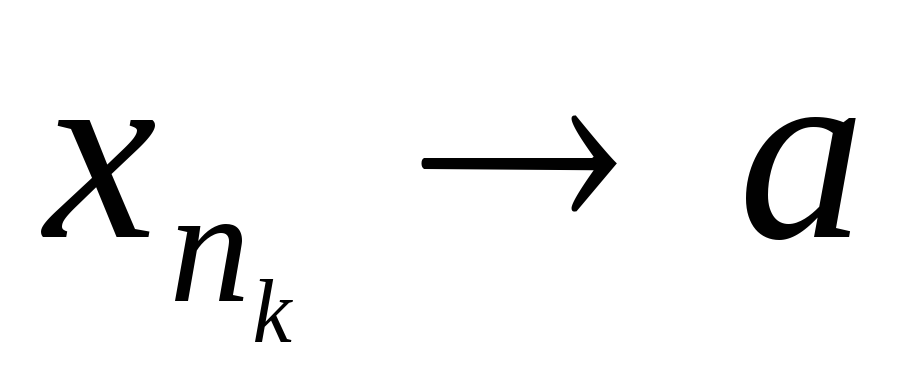 .
. -
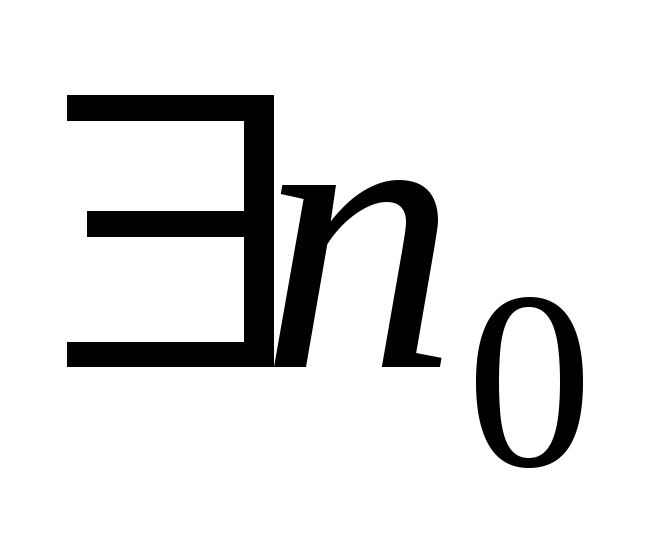 :
:
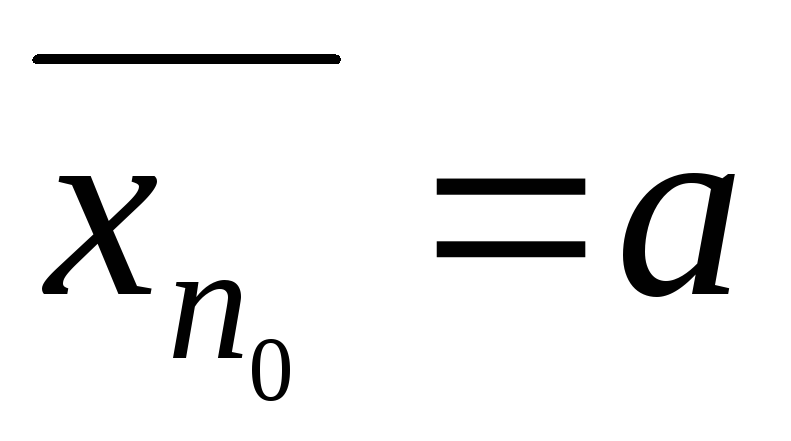
 всі
всі

 .
Тобто
.
Тобто
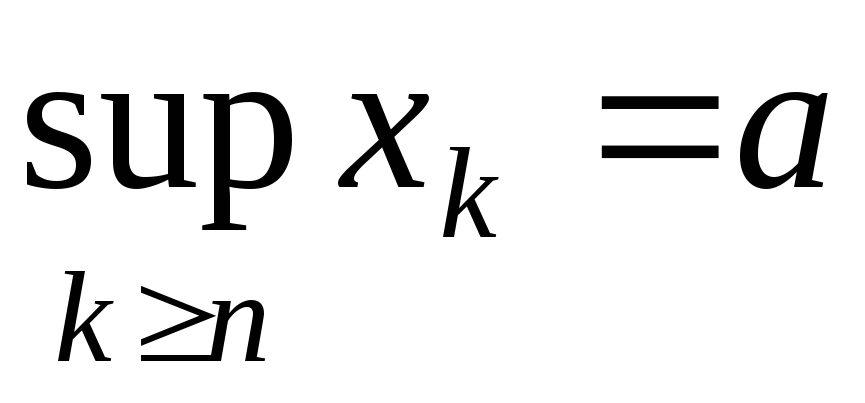

 є точкою дотикання кожної з множин
є точкою дотикання кожної з множин
 .
Тоді для
.
Тоді для
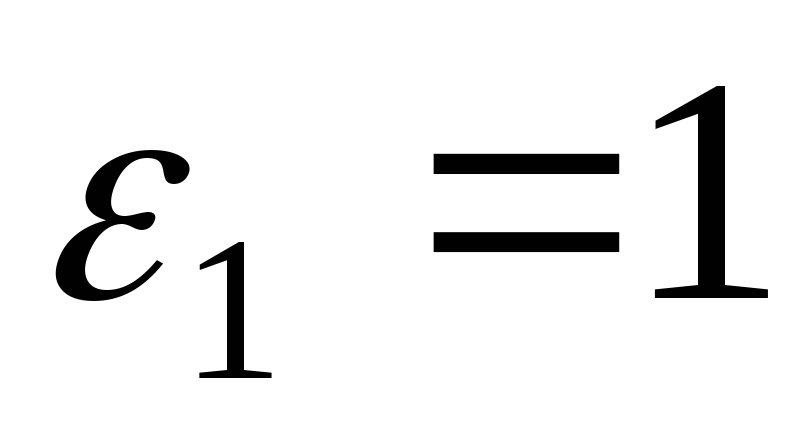 знаходимо
знаходимо
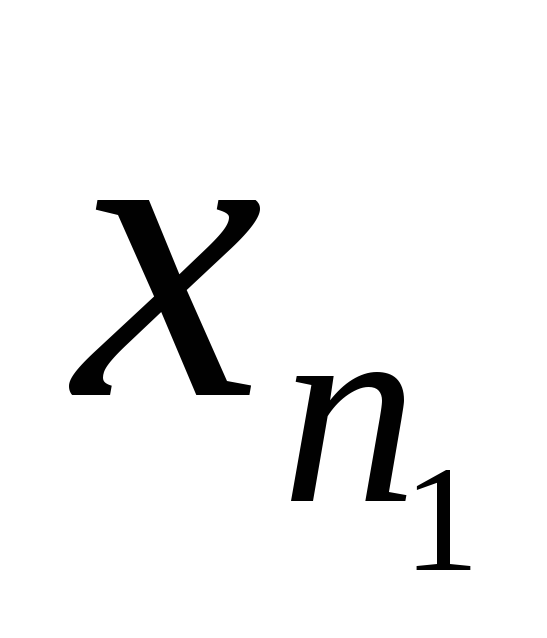 :
:
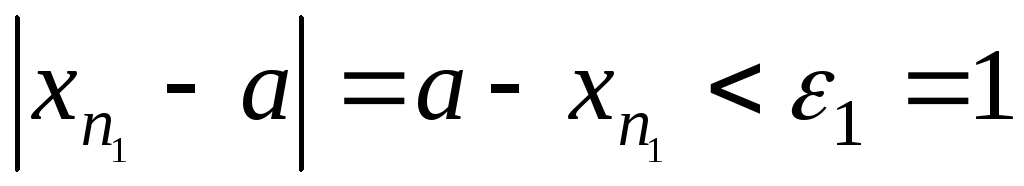
 ,
для
,
для
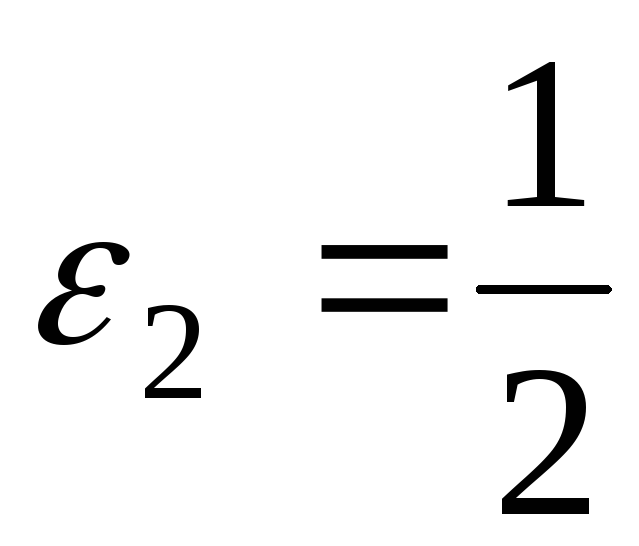 знаходимо
знаходимо
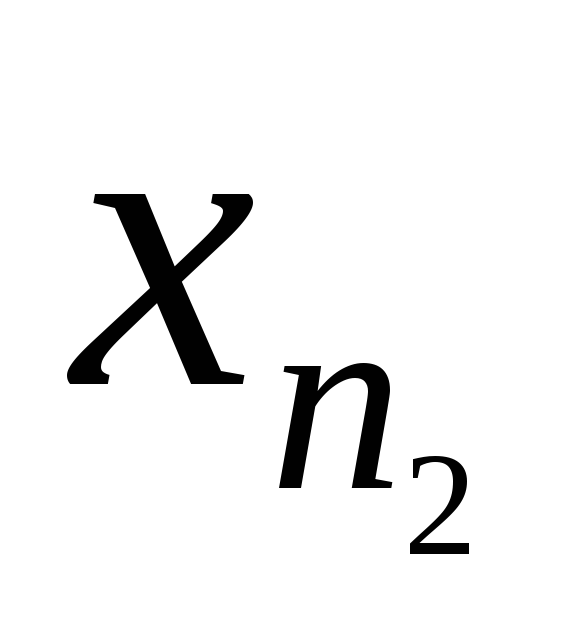 :
з множини
:
з множини
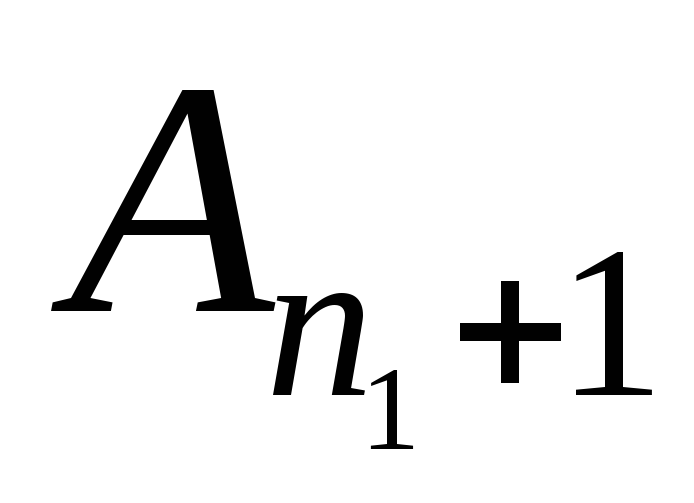
 :
:
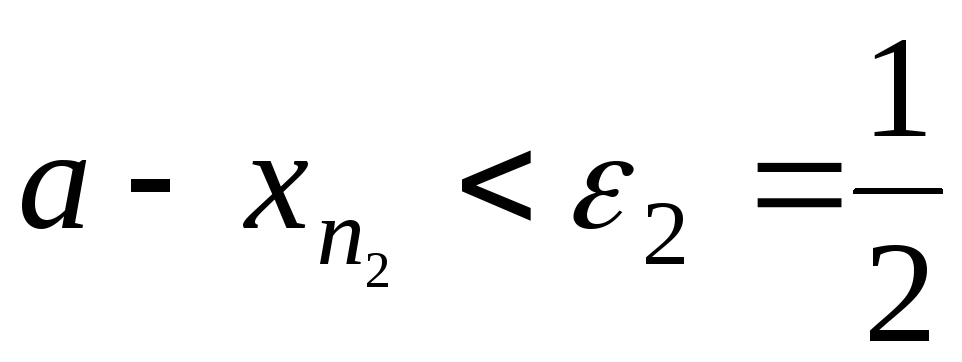 і т.д. Тоді для послідовності
і т.д. Тоді для послідовності

 ми
маємо, що
ми
маємо, що
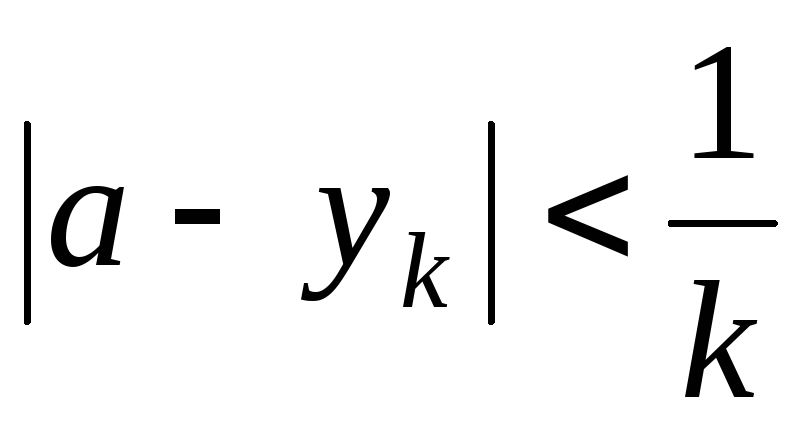

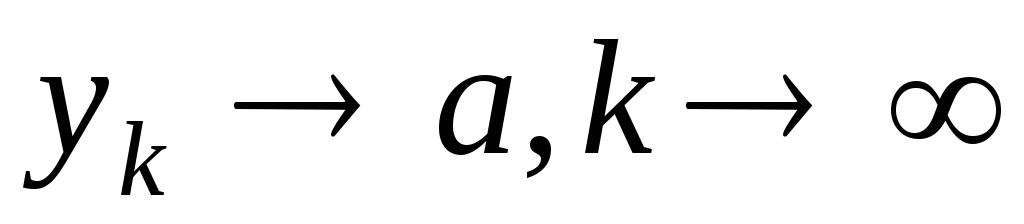 .
.
Аналогічно
доводиться твердження, що стосується
нижньої границі (або теж саме в просторі
![]() (тобто
(тобто
![]() )).
)).
Властивість доведена.
Властивість2. |
(Друга властивість верхньої (нижньої) границі). |
|
Верхня
(нижня) границя послідовності
|
![]() Доведення.
Доведемо знову лише для верхньої границі
методом від супротивного. Нехай
Доведення.
Доведемо знову лише для верхньої границі
методом від супротивного. Нехай
![]() і
і
![]() :
:![]() при
при
![]() .
Але тоді послідовність
.
Але тоді послідовність
![]() ,
яка монотонно не зростаюча та прямує
до
,
яка монотонно не зростаюча та прямує
до
![]() ,
починаючи з якогось номера
,
починаючи з якогось номера
![]() стане менше за
стане менше за
![]() .
А тоді
.
А тоді
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() - суперечність.
- суперечність.
Властивість доведена.
Теорема 3. |
(Про монотонну підпослідовність). |
|
З
будь-якої обмеженої послідовності
|
Доведення.
Нехай дано послідовність
![]() .
Якщо
.
Якщо
![]() серед членів послідовності
серед членів послідовності
![]() є
найбільший
є
найбільший
![]() ,
то послідовність
,
то послідовність
![]() є незростаюча (за властивістю верхньої
межі, що в цьому випадку співпадає з
найбільшим елементом), і вона є шуканою.
є незростаюча (за властивістю верхньої
межі, що в цьому випадку співпадає з
найбільшим елементом), і вона є шуканою.
Якщо
припустити протилежне, тобто
![]() серед членів
серед членів
![]() (3)
(3)
нема
найбільшого, то вибираємо монотонну
підпослідовність таким чином: за
![]() виберемо перший член останньої
послідовності (3),
який більше за
виберемо перший член останньої
послідовності (3),
який більше за
![]() ,
а далі за принципом математичної
індукції: нехай вже вибрано
,
а далі за принципом математичної
індукції: нехай вже вибрано
![]() ,
де
,
де
![]() .
Тоді в якості
.
Тоді в якості
![]() виберемо першій з членів послідовності
виберемо першій з членів послідовності
![]() ,
який більше за
,
який більше за
![]() .
Він існує, бо інакше серед членів
наведеної послідовності
.
Він існує, бо інакше серед членів
наведеної послідовності
![]() - найбільший, а тому і послідовність (3)
має
найбільший елемент. За принципом
математичної індукції побудовано
потрібну зростаючу послідовність
- найбільший, а тому і послідовність (3)
має
найбільший елемент. За принципом
математичної індукції побудовано
потрібну зростаючу послідовність
![]() ,
яка є підпослідовністю
,
яка є підпослідовністю
![]() .
.
Теорема доведена.
Теорема 4. |
(Больцано-Вейєрштрасса). |
|
З
кожної обмеженої послідовності
|
Доведення. Це є наслідком попередньої теореми, якщо згадати, що вибрана підпослідовність не лише монотонна, а ще й обмежена.
Теорема доведена.
Якщо
тепер розглянути всі послідовності в
просторі
![]()
![]() ,
то всі твердження та означення знову
мають місце, якщо вважати збіжною
послідовність, що прямує до
,
то всі твердження та означення знову
мають місце, якщо вважати збіжною
послідовність, що прямує до
![]() або
або
![]() .
Для необмеженої зверху (знизу) послідовності
.
Для необмеженої зверху (знизу) послідовності
![]() покладемо
покладемо
![]()
![]() .
Тоді легко зрозуміти, що кожна послідовність
має верхню та нижню границю, крім того,
кожна монотонна послідовність має
границю.
.
Тоді легко зрозуміти, що кожна послідовність
має верхню та нижню границю, крім того,
кожна монотонна послідовність має
границю.
Теорема 5. |
(Кантора). |
|
В
повному упорядкованому просторі
кожна спадна послідовність обмежених
замкнених та непорожніх множин
|
Доведення.
Виберемо
![]() в множині
в множині
![]() довільну точку
довільну точку
![]() .
Тоді послідовність
.
Тоді послідовність
![]() обмежена
обмежена
![]() - збіжна до деякої точки
- збіжна до деякої точки
![]() .
Очевидно, що
.
Очевидно, що
![]() є точкою дотикання
є точкою дотикання
![]() з замкненості
з замкненості
![]()
![]()
![]()
![]()
![]() .
.
Теорема доведена.
