Lektsii_Rubleva / Лекции Рублева-1 / Гл 08 Кратн_ кривол_н_йн_ та поверхнев_ _нтеграли / Пар 8-01 Об'єм м-вим_рного паралелеп_педа

3

Глава 8

Кратні, криволінійні та поверхневі інтеграли

1. Об’єм - вимірного паралелепіпеда

Нагадаємо, як визначається скалярний добуток в евклідовому просторі над полем дійсних чисел :

Функція 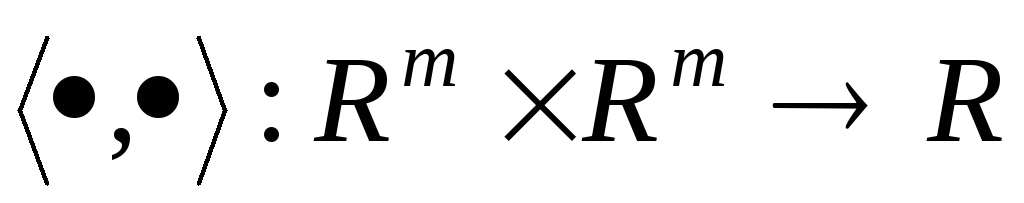називається скалярним добутком, якщо виконуються такі аксіоми:

1)	;
2)	;
3)	;
4)	.

Далі цей простір стає лінійним нормованим простором, якщо визначити норму таким чином .

Для простору скалярний добуток та норму визначають таким чином: , . (1)

З планіметрії відомо, що площа паралелограма дорівнює добутку основи (сторони) на висоту до цієї основи. Нехай паралелограм визначається парою векторів , тоді можна прийняти за основу, а за висоту – перпендикуляр, що опущений з кінця вектора на вісь вектора . Аналогічно, об’єм паралелепіпеду, що побудований на векторах є добуток площі основи (паралелограм, що будується на векторах ) на висоту до основи (перпендикуляр, що опущений з кінця вектора на площу основи).

Лінійною оболонкою скінченого (зліченого) набору векторів називається множина 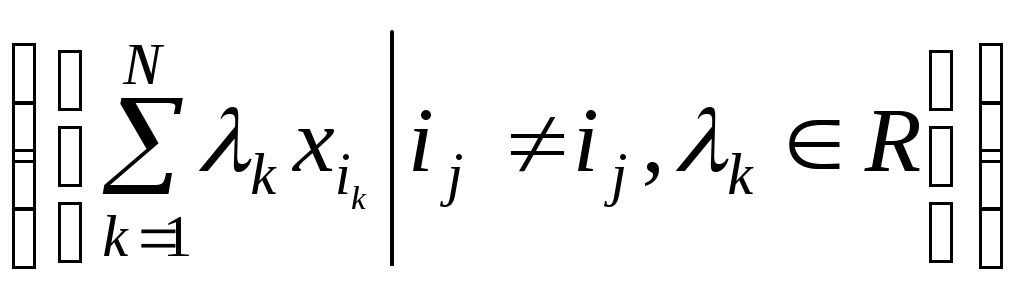та позначається .

Нехай задано систему векторів в евклідовому просторі . Позначимо через довжину перпендикуляра, що опущений з кінця вектора на підпростір , . Тоді - одновимірний об’єм; - двовимірний об’єм; ...; - - вимірний об’єм, тобто об’єм паралелепіпеда, що побудований на векторах . Згідно цього означення ми маємо таку формулу для обчислення об’єму - вимірного паралелепіпеда:

. (2)

Якщо , де . Тоді з умови маємо таке рівняння для знаходження : . Таким чином

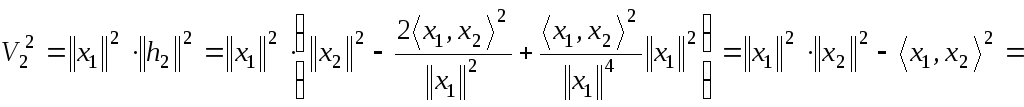
- визначник Грамма для векторів . Якщо до цього додати формулу , то можна припустити, що:

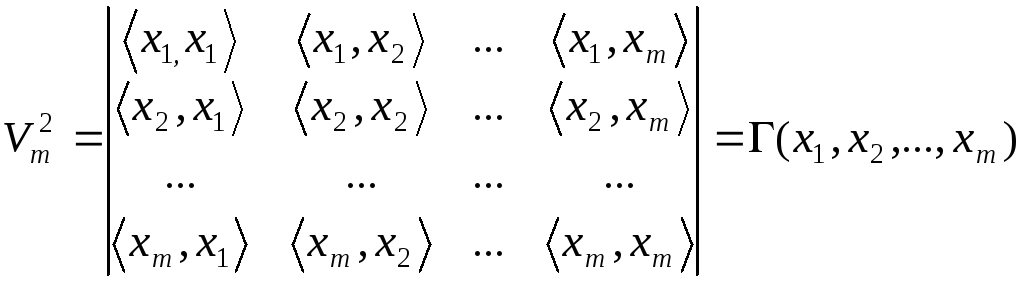. (3)

Теорема 1.	(Об’єм - вимірного паралелепіпеда)
	Об’єм - вимірного паралелепіпеда, що побудований на векторах обчислюється за формулою (3).

Доведення. Застосуємо до сукупності векторів процес ортогоналізації та зробити перехід у визначнику до скалярних добутків ортогональних векторів . Нехай , такий, що . Якщо у визначнику Грамма (3) замінити скрізь вектор на вектор (враховуючи, що ), то можемо скористатися лінійності при обчисленні визначників, одержимо, що цей визначник розбивається на два, у одного з яких (ті доданки, що будуть містити вектори ) є два пропорційні рядки, а тому він дорівнює нулеві. Далі повністю аналогічно для усіх векторів ми одержимо, що , але вектори - ортогональні, а тому . Далі достатньо побачити, що , а тому з останньої формули та рівності (2) одержимо потрібну рівність.

Теорема доведена.

Паралелепіпед називається - вимірним замкненим брусом.

Наслідок.	(Об’єм - вимірного замкненого бруса)
	Об’єм - вимірного бруса дорівнює:
	.	(4)

Доведення. З теореми 1, оскільки його можна вважати паралелепіпедом, що побудований на векторах , , ..., , його об’єм дорівнює , що й треба було довести.

Наслідок доведено.

Поряд з поняттям замкненого бруса розглянемо також його внутрішність, тобто множину . Її доречно назвати відкритим брусом, але поряд з такими брусами ми також будемо розглядати усі проміжні варіанти „брусів”, тобто таких множин , що задовольняють умову: . Усі такі множини ми також будемо називати - вимірними брусами та вважати, що їх об’єм обчислюється також за формулою (4). Серед цих множин нема відкритих (крім ) та замкнених (крім ).