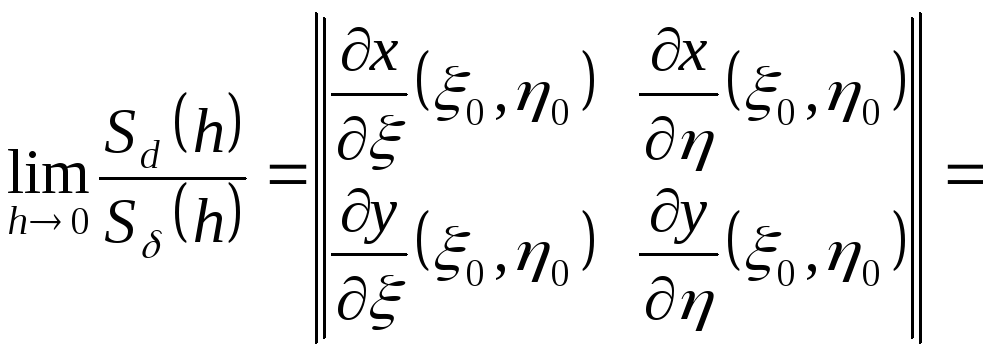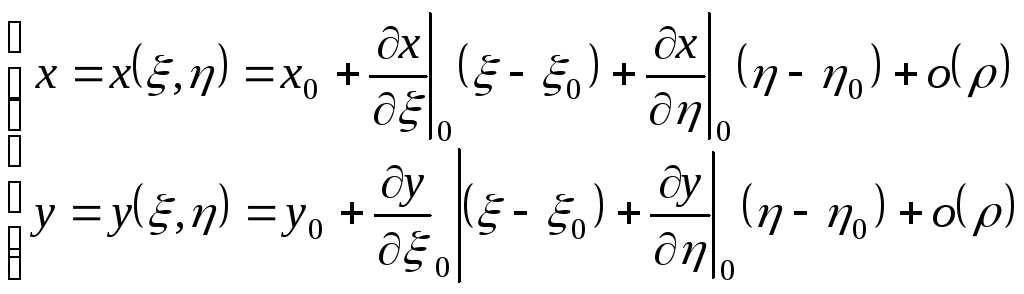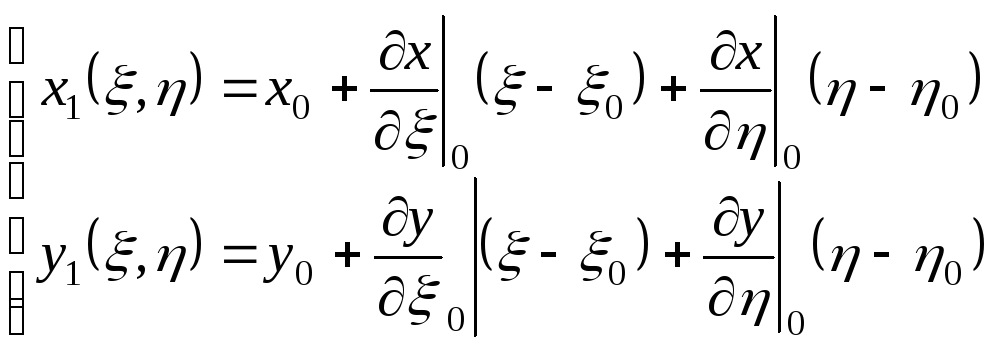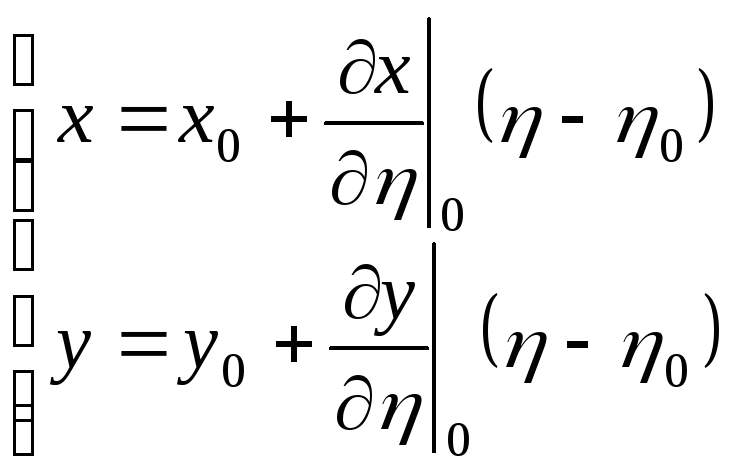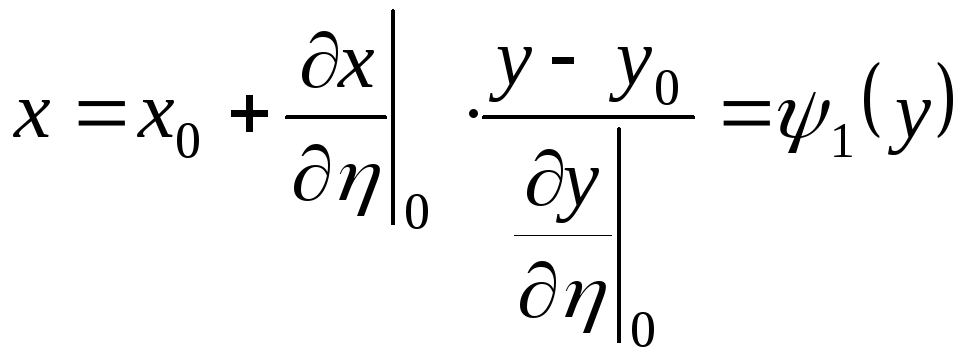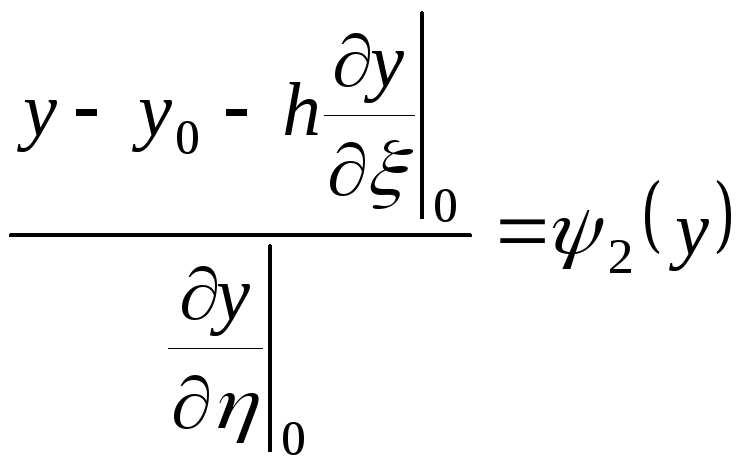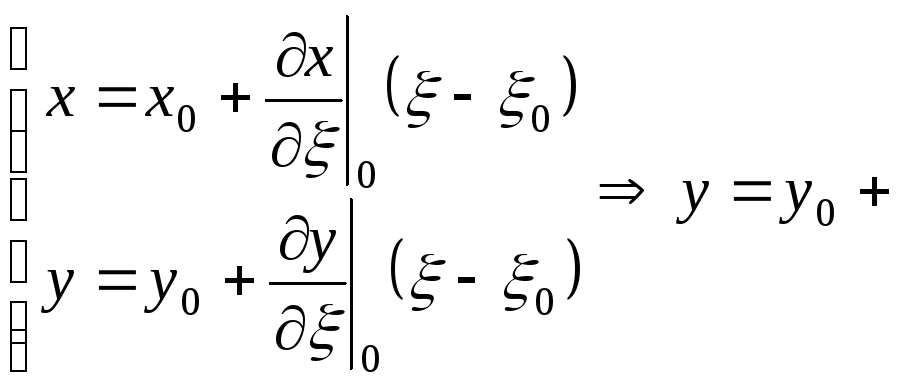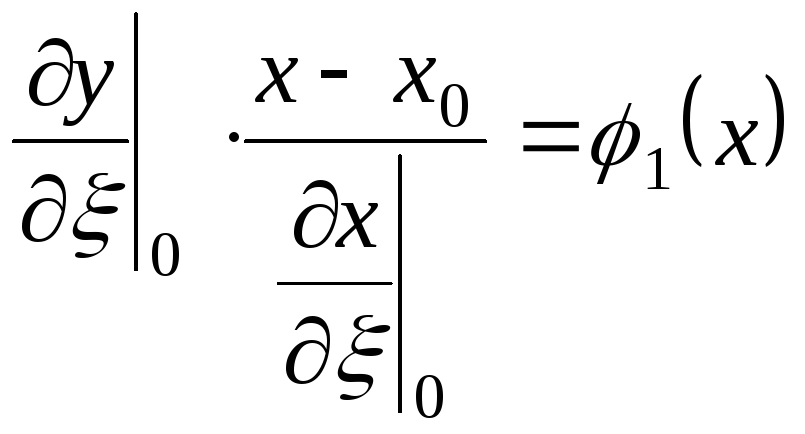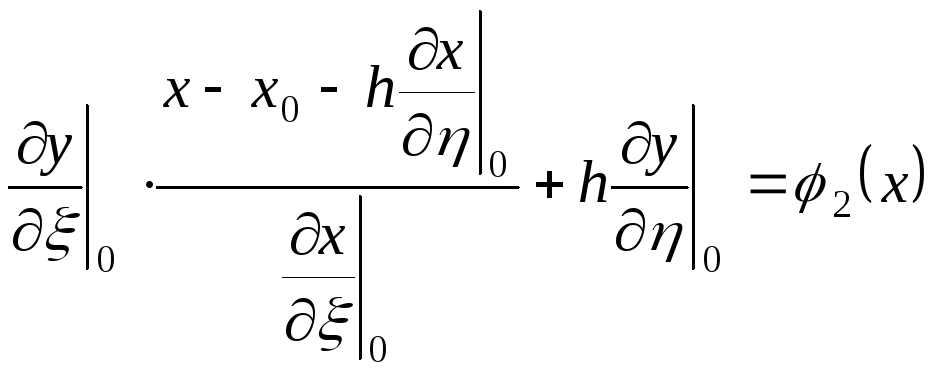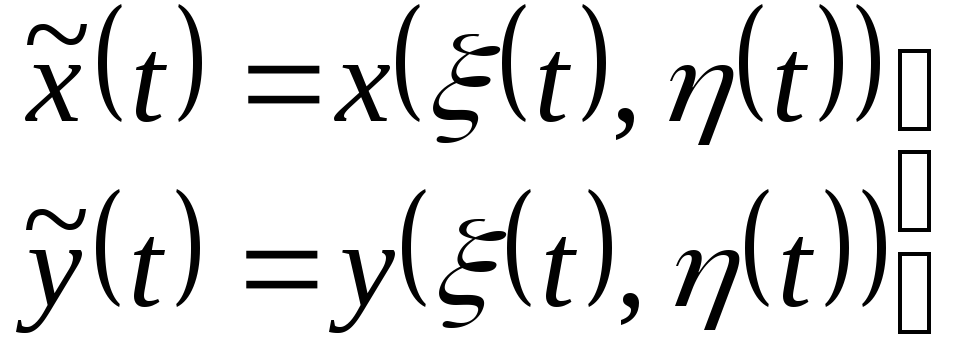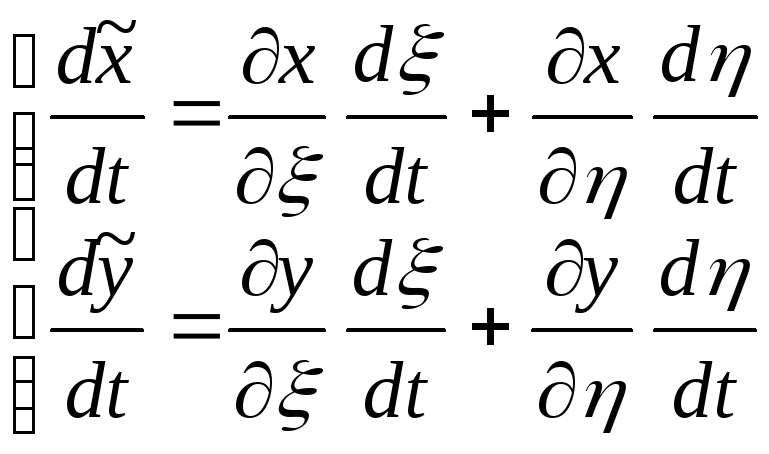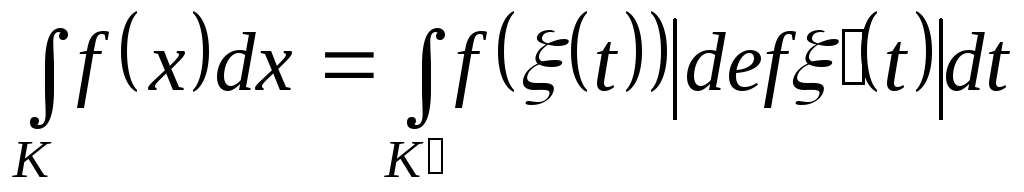Lektsii_Rubleva / Лекции Рублева-1 / Гл 08 Кратн_ кривол_н_йн_ та поверхнев_ _нтеграли / Пар 8-07 Зам_на зм_нних в _нтеграл_ Р_мана на компакт_

5

Глава 8

Кратні, криволінійні та поверхневі інтеграли

7. Заміна змінних в інтегралі Рімана на компакті

Розглянемо детально заміну змінних в подвійному інтегралі. Нехай в нас є дві системи координат і . Нехай в площині є область , яка при відображенні

(10.1)

переходить в область на площині . Виберемо квадрат в області , де , , , і позначимо його площу . Нехай площа криволінійного чотирикутника , який є образом квадрата при відображенні (10.1).

Означення .	Бієктивне відображення називається гомеоморфізмом, якщо і неперервні.
Означення .	Гомеоморфне відображення замкненої області на замкнену область , яке переводить внутрішні точки у внутрішні, граничні – у граничні, називається регулярним, якщо і неперервно диференційовані відповідно на та .

Звідси безпосередньо слідує, що якобіани не обертаються в нуль, бо добуток (якобіана на якобіан ) дорівнює одиниці.

Теорема 1.	(про геометричний зміст модуля якобіана)
	Якщо (10.1) гомеоморфне регулярне відображення замкненої обмеженої області на замкнену обмежену область , то для довільної внутрішньої точки має місце гранична рівність:
		(10.2)

Доведення. З регулярності відображення (10.1) слідує, що , а тому відмінні від нуля обидва елементи однієї з діагоналей даного якобіана. Нехай, наприклад, , (10.3)

З диференційованості (10.1) можемо записати формулу Тейлора в точці і її околі:

(10.4)

Тут під можемо покласти будь-яку з метрик, вони всі еквівалентні, найчастіше вживаємі. , , .

Разом з відображенням , розглянемо лінійні відображення, які з’являються з (10.4) відкиданням .

(10.5)

Подивимось, у що перейдуть прямі 1), 2) , 3),

4) при відображенні (10.5), в наслідок його лінійності всі прямі 1)-4) перейдуть в прямі, і прямі 1) і 2) паралельні, то і їх образи будуть паралельними, аналогічно для прямих 3) і 4) та їх образів.

1)

- параметрична форма прямої з параметром :

( з умови (10.3))

(10.6а)

2)

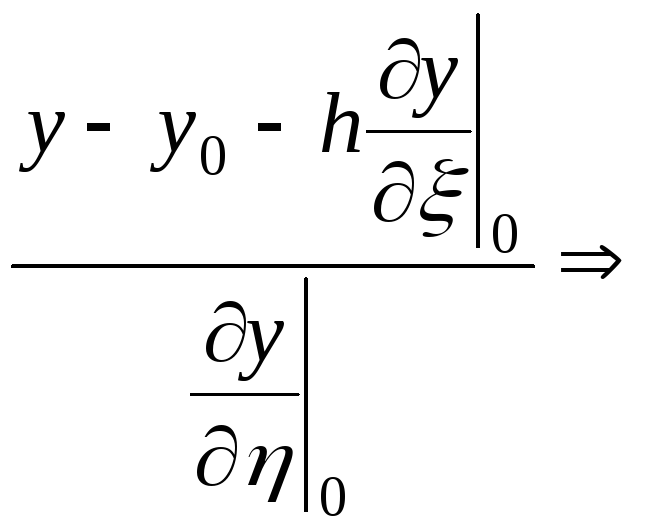
(10.6б)

3)

(10.6в)

4)
		(10.6г)

Легко переконатися, що прямі (10.6а-г) проходять через точки: , ,

Прямі (10.6а-г) утворюють паралелограм , знайдемо його площу:

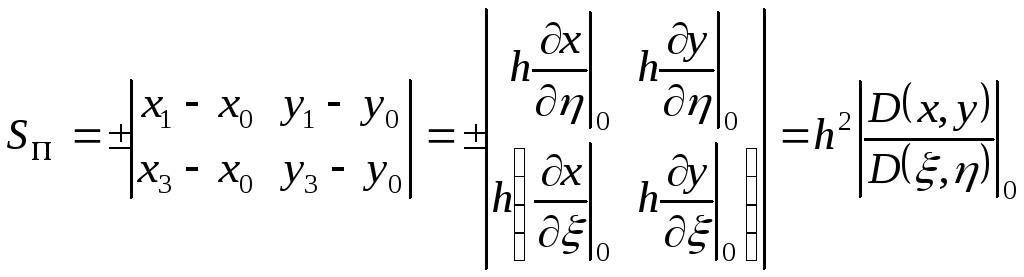(10.7)

Розглянемо тепер криволінійний чотирикутник, який утворюється образами прямих 1)-4) при перетворенні (10.4) (чи (10.1)- що є тим самим).

1)

Звідси, виключаючи параметр, одержимо:

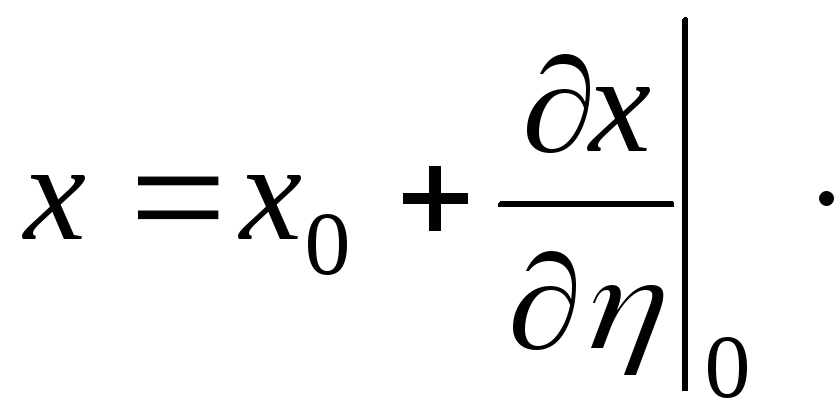
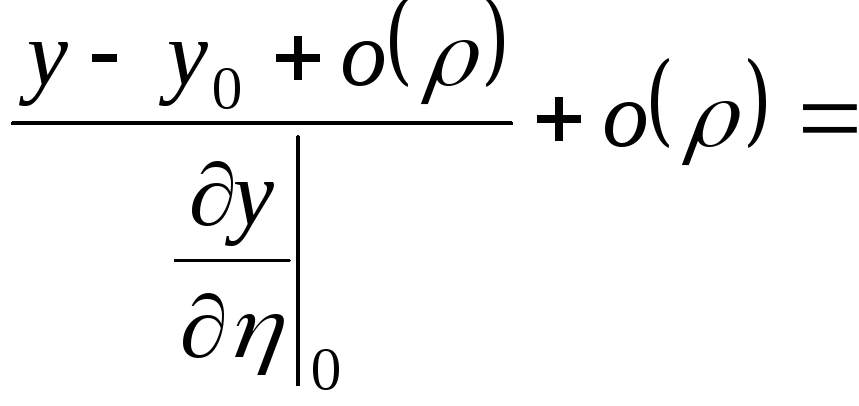
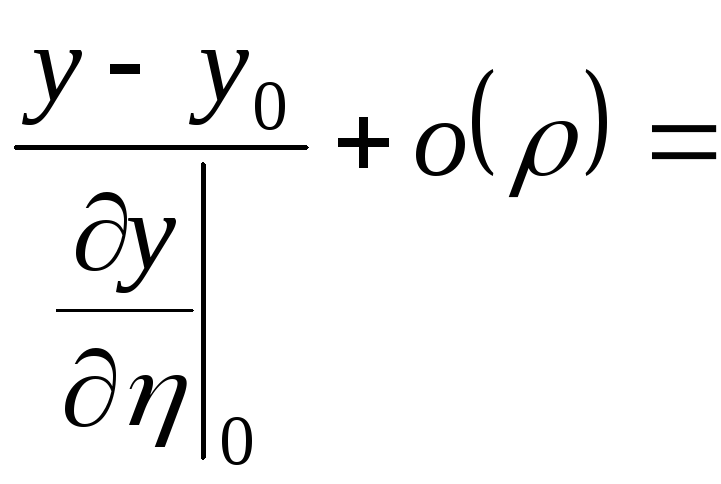
Аналогічно:

Тепер розглянемо різницю площ криволінійного чотирикутника і паралелограма :

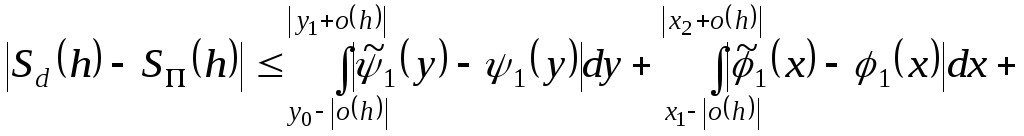
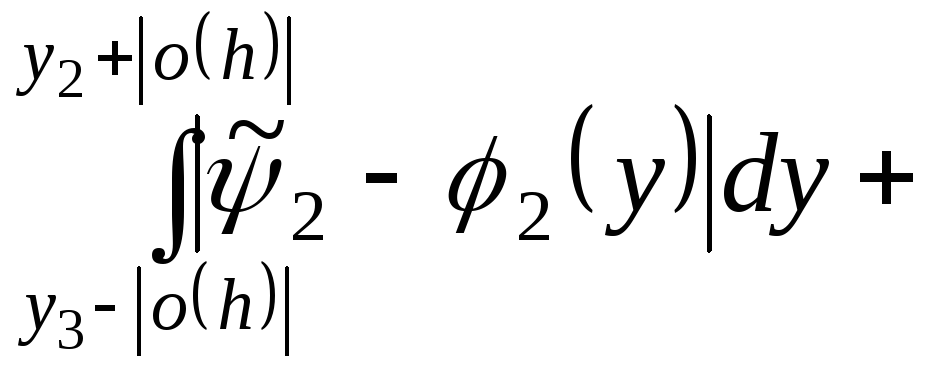
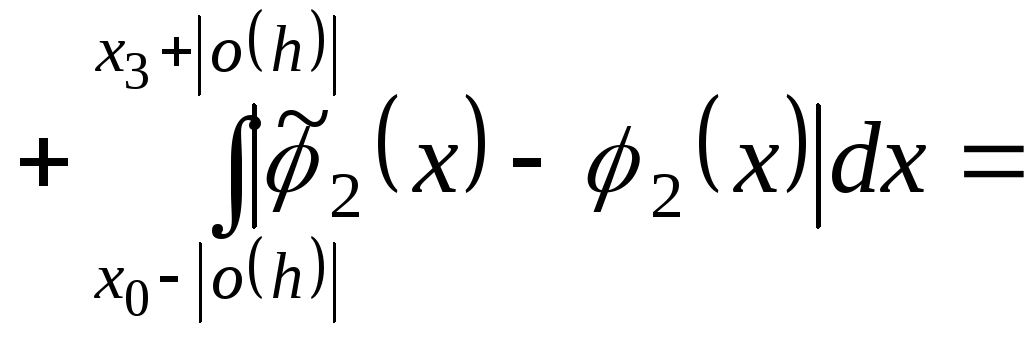
, т.я..

Звідси очевидно одержуємо (ділимо на і переходимо до границі при ):

(10.8)

Теорему доведено.

Звідси можемо записати:

Зауваження		В формулі (10.4) ми маємо, що функції розкладені за формулою Тейлора, при цьому функції
неперервні, а внаслідок того, що - компакт, то вони всі рівномірно неперервні, звідси слідує, що нескінченно малі можна представити у вигляді , де рівномірно прямує до нуля при , тому останню формулу можна записати у вигляді:
			(10.9)

Нехай - проста гладка крива, яка параметрично задається умовами:

.

Нехай вона знаходиться в , тоді при регулярному гомеоморфному відображенні (10.1) вона знов таки перейде в просту гладку криву :

(10.10)

(крива проста – без само перетинів, замкнена проста – початкова і остання точки співпадають.)

проста, (10.1) – регулярне і гомеоморфне - проста.

- гладка з умов:

(10.11)

З гладкої і регулярності (10.1).

Доведемо, що .

Припустивши, що: для деякого підставивши цю умову в (10.11):

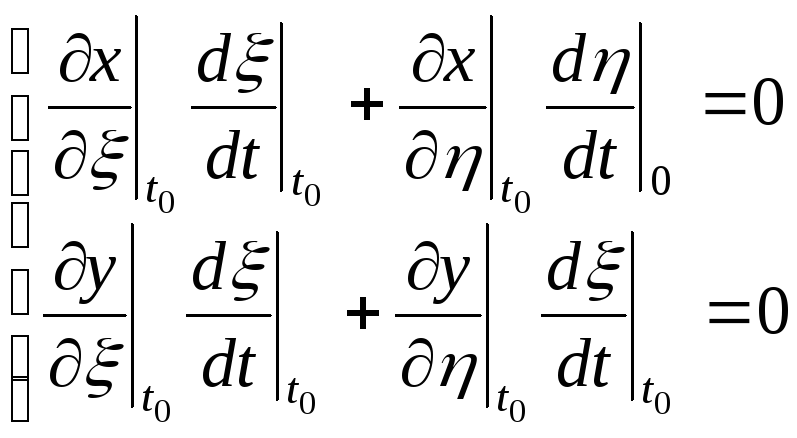. За умовою в жодній точці або , тобто однорідна система має нетривіальний розв’язок, звідки слідує, що визначник системи нульовий, 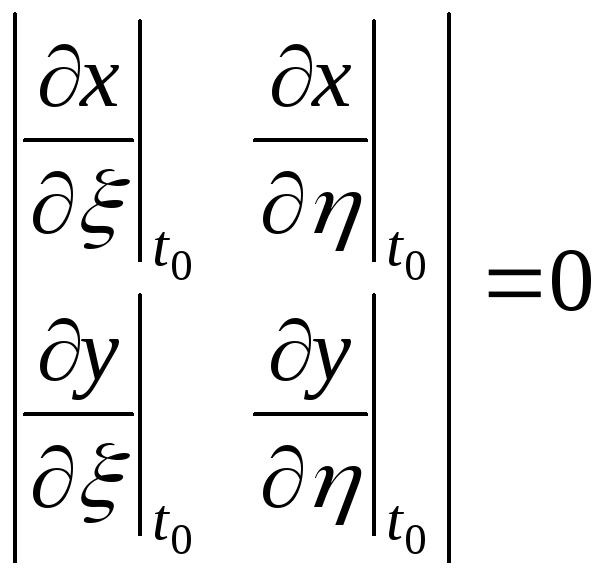, а це не відповідає умові регулярності відображення (10.1).

Теорема 2.	(про заміну змінних в подвійному інтегралі)
	Нехай в замкненій обмеженій області визначена функція яка або неперервна всюди в , або обмежена в і міра її точок розриву є нуль. Нехай (10.12) бієкція множини на область площини , яке є регулярним в деякій області , що містить в собі разом зі своїм оточенням. Тоді має місце така формула заміни змінних в подвійному інтегралі:
		(10.13)
	де (10.14) є обернене до (10.12) відображення.

Доведення. Нехай ми розбили область на квадрати зі стороною , - множина всіх таких квадратів (при достатньо малому ), які містяться в , образи є множина . Тоді з формули (10.9) ми маємо: . Утворимо суму:

.

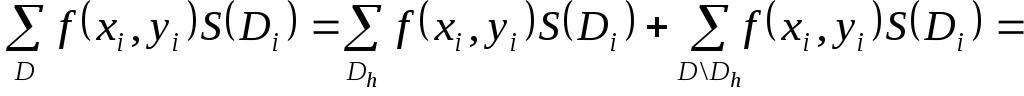
Переходимо в останній рівності до границі при і маємо, що , а те, що залишилося, прямує до відповідних інтегралів, які записані в обох частинах (10.13).

Чому саме .

внаслідок рівномірного прямування , а і ось чому функції обмежені числом , якобіаном так само, числом , тоді , звідки при , аналогічно для .

Тепер без доведення сформулюємо загальний випадок теореми:

Теорема 3.	(про заміну змінних в інтегралі Рімана)
	Нехай компакт, функція - неперервна (або обмежена з мірою Лебега точок розриву ), регулярне гомеоморфне відображення компакта на , що є регулярним на множині , що містить в собі з оточенням. Тоді має місце формула:
		(10.15)