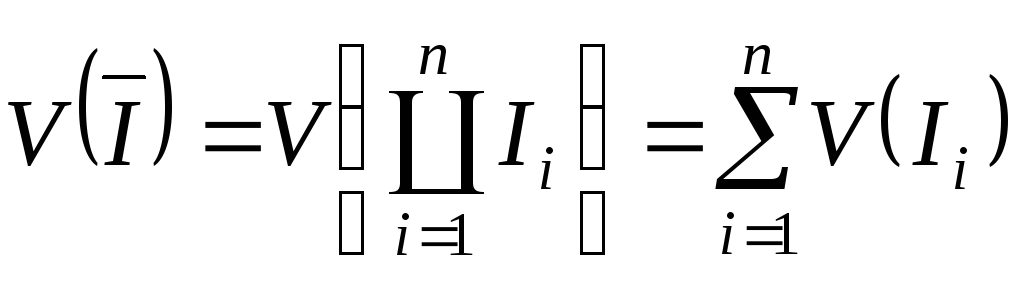Lektsii_Rubleva / Лекции Рублева-1 / Гл 08 Кратн_ кривол_н_йн_ та поверхнев_ _нтеграли / Пар 8-02 _нтеграл Р_мана на нагруж метрич простор_

3

Глава 8

Кратні, криволінійні та поверхневі інтеграли

2. Інтеграл Рімана на нагруженому метричному просторі

Система підмножин множини називається півкільцем, якщо виконуються такі умови:

1) ;

2) якщо , то ;

3) якщо , то існують такі множини , що виконується рівність: .

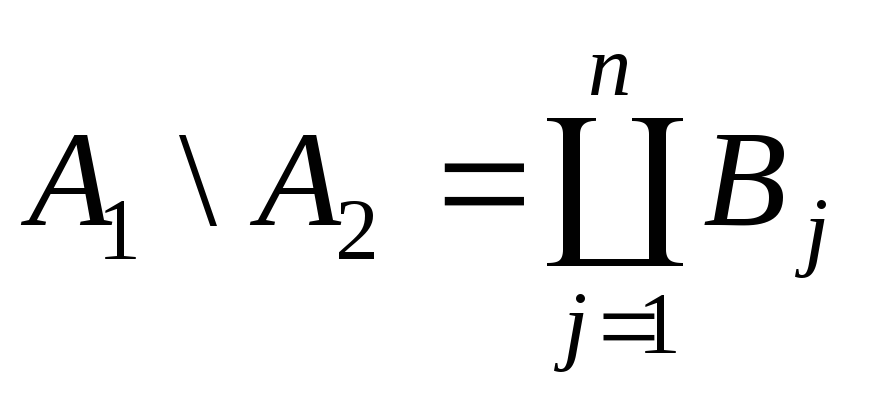(Значком позначається диз’юнктне об’єднання множин, тобто об’єднання попарно неперетинаючихся множин).

Нехай - метричний простір, а задовольняє умови:

а) існує зображення множини у вигляді скінченого диз’юнктного об’єднання множин із , з діаметрами, що не перевищують ;

б) для кожної множини визначено невід’ємне число так, що з умови , де слідує, що .

Число називається мірою множини , самі множини при виконанні умов 1)-3), а), б) називаються комірками, метричний простір називається нагруженим метричним простором, а півкільце з мірою комірок - нагруженням простору.

Приклад 1.	, - множина всіх проміжків типу , , , , що містяться в . Якщо визначити , де - будь-який з наведених проміжків.
Приклад 2.	, - множина всіх брусів типу , що містяться в . Якщо визначити , де - будь-який з наведених проміжків.

Нехай - нагружений метричний простір, , де - комірки. Множина називається розбиттям множини на комірки , число називається діаметром розбиття .

Нехай - числова функція, що визначена на нагруженому метричному просторі . Візьмемо довільні точки , множину яких позначимо через і утворимо суму

, (1)

яку назвемо інтегральною сумою Рімана для функції на множині .

Кажуть, що інтегральні суми мають границю , що записується рівністю: : .

Якщо при існує , , то функція називається інтегрованою за Ріманом на множині , а число - інтегралом Рімана цієї функції на множині з нагруженням і позначається

. (2)

Множину усіх функцій, інтегрованих за Ріманом на нагруженому метричному просторі позначимо .

Властивості.	(Інтеграла Рімана на нагруженому метричному просторі)
1.	(Інтеграл Рімана від сталої)
	Функція інтегрована за Ріманом на і
	.	(3)
2.	(Лінійність інтегралу Рімана)
	Якщо функції інтегровані за Ріманом на , то функція і виконується рівність:
	.	(4)
3.	(Обмеженість інтегрованої функції)
	Якщо функція інтегрована за Ріманом на , то - обмежена функція.
4.	(Інтеграл Рімана від нерівних функцій)
	Якщо і , то
	.	(5)

Доведення. Властивості 1,2,4 доводяться простим переходом до границі в інтегральних сумах. Наприклад, властивість 4:

(обидві границі за умовою існують) .

Доведемо властивість 3 методом від супротивного. Припустимо, що - необмежена, тоді при кожному розбитті існує комірка, в якій вона необмежена. Будемо точку з цієї комірки вибирати останньою. Вибравши на -му кроці усі точки, для них нехай частина інтегральна суми дорівнює , тоді підберемо точку з тієї комірки де функція необмежена таким чином, щоб , а тому інтегральні суми не мають границі при деякому виборі точок розбиття, що суперечить інтегрованості за Ріманом на функції .

Властивості доведено.

Наслідок 1.	(Модуль інтегралу Рімана)
	Якщо функція : , то
	.	(6)
Наслідок 2.	(Двобічна оцінка інтегралу Рімана)
	Якщо функція та
	.	(7)

Зрозуміло, що ці наслідки безпосередньо слідують з властивості 4. Зокрема з останнього наслідку ми маємо, що завжди виконується нерівність:

. (8)

Розглянемо брус . За допомогою гіперплощин, рівняння яких мають вигляд , розіб’ємо брус на менших брусів (комірок) , які попарно не перетинаються. Це означає, що точки межі перетину двох брусів можна відносити до будь-яких з двох (чи більше) брусів, припустимо, можна домовитися, що межа належить тому брусові, який має менший номер при лексикографічному переліку. Це розбиття називається сітковим розбиттям брусу та позначається . Для ситкового розбиття брусу виконується рівність: . Вважаємо, що об’єм кожної комірки дорівнює об’єму .

Лема 1.	(Про сіткове розбиття брусу)
	Якщо - сіткове розбиття бруса , то для об’єму цих брусів виконується рівність:
		(9)

Доведення очевидно й слідує з диз’юнктного розбиття бруса.

Ця лема встановлює властивість адитивності об’єму, який тепер виступає в якості міри на брусі . Сам брус стає нагруженим метричним простором, комірки з їх об’ємом стають його нагруженням. Після таких визначень можна визначити інтеграл Рімана брусі, як на нагруженому метричному просторі. Нехай - обмежена функція, що визначена брусі , тоді:

, (10)

де - діаметр сіткового розбиття брусу на комірки , - сукупність проміжних точок, . Інтеграл в лівій частині рівності (10) позначають також символом . Множину всіх функцій, що інтегровані за Ріманом на брусі , позначають символом .