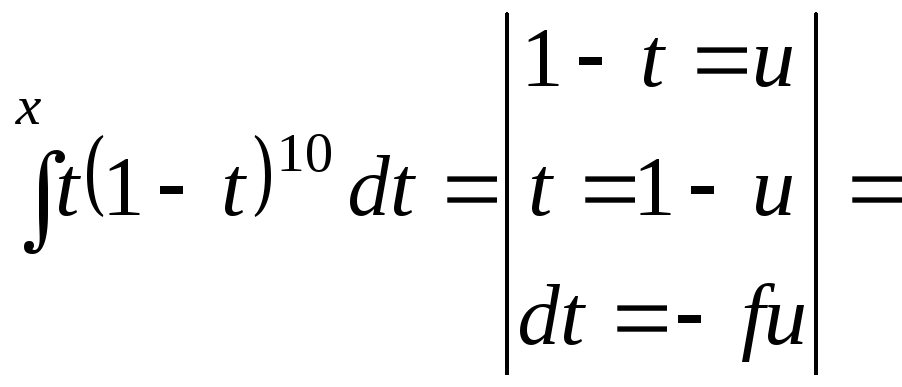Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Киевский национальный университет им. Т. Шевченко

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Пар 3-01 _нтеграл Ньютона-Лейбн_ца

.doc

Скачиваний:

Добавлен:

19.03.2015

Размер:

349.7 Кб

Скачать

☆

Глава 3

Інтеграл Ньютона-Лебніца

1. Визначення інтеграла Ньютона-Лейбніца.

Нехай у функції множина не має ізольованих точок. Функція називається первісною функції , якщо і .

Властивість 1.

Якщо первісна функції , то функція теж буде первісною функції .

Внаслідок останньої властивості, первісна визначається неоднозначно, а тому спеціального позначення не має. Лейбніц запропонував для всіх первісних позначення , який одержав назву невизначеного інтегралу.

Теорема 1.	(Зв’язок між різними первісними).
	Якщо для функції первісними є функції , то : .

Доведення. Розглянемо функцію , , тоді .

Теорему доведено.

Таблиця первісних:

Функція	Первісна	Функція	первісна
1)		2)
3)		4)
5)		6)
7)		8)
9)		10)
11)		12)
13)		14)
15)		16)

Вже з визначення та найпростіших властивостей первісних, стає зрозумілим, що є певна двозначність в понятті первісних:

або це деяка первісна, фіксована чи довільна,
або це множина всіх первісних.

Кожне з цих визначень має певний недолік. В першому випадку недоліком є неоднозначність визначення первісної, а в другому – незрозумілість операцій з первісними, як з множиною.

Функція називається інтегрованою в розумінні Ньютона-Лейбніца, якщо вона має первісну. Покладемо при цьому

, тоді функція називається інтегралом Ньютона-Лейбніца з фіксованою нижньою межею. Значення називається визначеним інтегралом Ньютона-Лейбніца, де називається змінною інтегрування.

Теорема 2.	(Формула Ньютона-Лейбніца).
	Нехай інтегрована в розумінні Ньютона-Лейбніца функція, якщо - її довільна первісна. Тоді існує визначений однозначно, і виконується рівність:
	,	(1)
	яка називається формулою Ньютона-Лейбніца.

Доведення теореми. Нехай первісна, тобто за означенням . Однозначність очевидна.

Теорему доведено.

Властивості.	(Інтеграла Ньютона-Лейбніца).
	Якщо інтегрована в розумінні Ньютона-Лейбніца функція, то виконуються рівності:
1)	- перестановка меж інтегрування;
2)	- адитивність по межах інтегрування;
3)	;
4)	- диференціювання по верхній та нижній межах інтегрування.

Доведення теореми. Нехай первісна функції , тоді, за формулою Ньютона-Лейбніца (1), одержимо:

1)	.
2)	…
3)	, аналогічно 4).

Теорему доведено.

Теорема 3.	(Лінійність інтеграла).
	Якщо функції інтегровані в розумінні Ньютона-Лейбніца на , тоді функція також інтегрована в розумінні Ньютона-Лейбніца на і виконується рівність:
	.

Доведення теореми. Якщо і первісні функції і , то інтегрована в розумінні Ньютона-Лейбніца. Нехай , .

Теорему доведено.

Теорема 4.	(Про заміну змінної).
	Нехай для функцій , виконуються умови:
1)	;
2)	диференційована ;
3)	- інтегрована в розумінні Ньютона-Лейбніца на .
	Тоді функція також інтегрована і виконується рівність:
		(2)

Доведення теореми. Нехай - первісна функції , і інтегрованість за Ньютоном-Лейбніцем, а також .

Теорему доведено.

Приклад 1.

Теорема 5.	(Інтегрування частинами).
	Нехай для функцій , диференційовані на множині , функція інтегрована на цій множині в розумінні Ньютона-Лейбніца, то функція також інтегрована і виконується рівність:
	, яка називається формулою інтегрування частинами.	(3)