11

Министерство общего и профессионального

ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

______________________________

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ОТКРЫТЫЙ УНИВЕРСИТЕТ

КОЛОМЕНСКИЙ ИНСТИТУТ

«УТВЕРЖДЕНО» Учебно-методическим Советом КИ МГОУ Председатель совета ______________________ А. М. Липатов «____»___________ 2003 г.

Трушков А. С.

Родионов К.А.

ВЫСШАЯ МАТЕМАТИКА

И Н С Т Р У К Ц И Я

для выполнения лабораторной работы

Множественная линейная и нелинейная

корреляция и регрессия

2003 г.

СОДЕРЖАНИЕ

1.	Введение	3
2.	Модель парной регрессии	3
3.	Модель множественной регрессии	7
4.	Порядок выполнения лабораторной работы	10
4.1.	Определение коэффициентов регрессии	11
4.2.	Определение коэффициента детерминации	11
4.3.	Оценка значений дисперсии	15
4.4.	Определение дисперсии оценок i	15
4.5.	Проверка значимости коэффициентовi	15
4.6.	Построение доверительных интервалов для коэффициентов регрессии	15
4.7.	Проверка значимости уравнения регрессии	15
4.8.	Построение диаграммы	16
5.	Задание к лабораторной работе	16
6.	Литература	17

1. Введение

Лабораторная работа выполняется с помощью электронных таблиц Microsoft Excel в операционной среде Windows 95. В рабочей книге Excel используется программный код, написанный на алгоритмическом языке Visual Basic for Application (VBA), с помощью которого по заданному номеру варианта генерируется выборка со случайным объемом наблюдений на основе розыгрыша двумерной случайной величины (X, Y) по заданному уравнению регрессии Y = f(X) и дисперсии ошибки. C помощью программы производится линейный и нелинейный регрессионный анализ. Целью лабораторной работы является освоение алгоритмов статистических методов обработки наблюдений: вычисление коэффициентов регрессии, построение линейной и нелинейной регрессии, определение значимости коэффициентов регрессии, анализ дисперсий, расчет коэффициента детерминации, определение доверительных интервалов для коэффициентов регрессии и построение диаграммы наблюдений случайной величины.

2. Модель парной регрессии

Пусть есть результаты некоторого эксперимента ( x_i , y_i ), i = 1, ... , n. Надо подобрать (“подогнать”) функцию , зависящую от параметра , наилучшим образом описывающую экспериментальные точки( x_i , y_i ).

Сначала рассмотрим линейную функцию y = f(x) = ax + b. Здесь надо подобрать числа a и b. Критерием качества “подгонки” кривой выберем минимум функционала:

. (1)

Данный принцип называется методом наименьших квадратов и является одним из самых распространенных методов подбора функциональной зависимости, наилучшим образом описывающим эмпирические данные.

Используя необходимые условия экстремума:

, (2)

получим следующие значения оптимальных параметров функции “подгонки”:

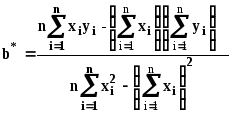, (3)

.

Очевидно, что , то есть график полученной прямой проходит через точку, где:

- выборочное среднее переменной Х,

- выборочное среднее переменной Y.

Если обозначить: ,- отклонения случайных величин от своих средних выборочных значений, то:.

В этом случае: 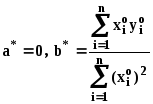. (4)

Введем обозначения:

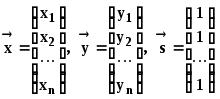, (5)

Тогда - вектор “подогнанных” с помощью регрессионного уравнения значенийу, лежащий в плоскости (гиперплоскости) векторов и;- вектор разности между выборочными значениямиу и “подогнанными” с помощью функции y = f(x). Наилучшее приближение кбудет, если длина векторабудет минимальной. Это условие выполняется, если векторперпендикулярен обоим векторами, то есть:

,  . (6)

Условие (6) эквивалентно равенству нулю двух скалярных произведений:

= 0 и = 0. (7)

Символ “ ^{т ”} - означает, что соответствующий вектор или матрица транспонированы.

Обозначим

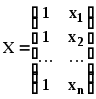- матрица размера n2, (8)

- вектор-строка размера 21. (9)

Тогда . (10)

Условие ортогональности вектора к плоскости векторовив данных обозначениях примет вид:

. (11)

Проведем преобразование этого уравнения:

(12)

Можно показать, что уравнение (12) для коэффициентов регрессионного уравнения a и b совпадает с полученными ранее по методу наименьших квадратов формулами (3).

Пусть реальное (теоретическое) уравнение зависимости y от х имеет вид:

y = a + bx + , (13)

где х - неслучайная (детерминированная) величина,

у и  - случайные величины.

Величина у называется объясняемой (зависимой) переменной, х - объясняющей (независимой) переменной или регрессором,  - случайной компонентой, уравнение (13) - регрессионным уравнением. Будем считать, что случайная компонента распределена по нормальному закону   N(0, ), где  ² - дисперсия ошибок.

По данным наблюдений следует найти оценки a^* и b^* для коэффициентов уравнения регрессии и s² - для дисперсии ошибок  ².

Имеет место теорема Гаусса-Маркова, утверждающая, что при использовании метода наименьших квадратов для определения оценок a^* и b^* коэффициентов уравнения регрессии по формуле , полученные оценки являются несмещенными и эффективными в классе всех несмещенных оценок (то есть имеют наименьшую дисперсию).

В соответствии с теоремой Гаусса-Маркова оценки a^* и b^* распределены по нормальному закону: a^*  N(a, _a), b^*  N(b, _b), при этом имеют место следующие формулы для дисперсий оценок a^* и b^*:

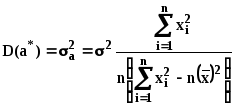, (14)

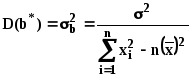. (15)

Корреляционный момент (ковариация) коэффициентов регрессии равна:

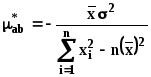. (16)

Для оценки дисперсий используются следующие формулы:

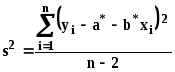(17)

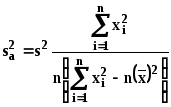, (18)

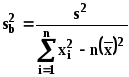. (19)

В соответствии с теоремой Гаусса-Маркова принимается, что случайная величина имеет распределение² с (n - 2) степенями свободы.

При проверке гипотезы:

H₀: b = b₀ (20)

H₁: b  b₀

используется статистика , имеющая распределение Стьюдента с(n - 2) степенями свободы.

Доверительный интервал для коэффициента b с надежностью  имеет вид:

, (21)

где t_ - квантиль распределения Стьюдента, определяемый из условия:

P( | t | < t_ ) = . (22)

Аналогично доверительный интервал для коэффициента а с надежностью  имеет вид:

. (23)

Рассмотрим вариацию (дисперсию) значенийy_i вокруг среднего значения. Можно показать, что:

(24)

или

TSS = ESS + RSS, (25)

где TSS - вся дисперсия - total sum of squares,

ESS - необъясненная часть дисперсии - errors sum of squares,

RSS - объясненная часть дисперсии - regression sum of squares.

Коэффициентом детерминации (или долей объясненной дисперсии) называется величина:

(26)

Очевидно, что 0  R²  1. Если, R² = 0, то регрессия не улучшает качество прогноза у по сравнению с тривиальным: . ЕслиR² = 1, то это означает точную “подгонку”: все наблюдаемые точки лежат на регрессионной кривой.

Проверку значимости коэффициента b уравнения регрессии можно проверить с использованием критерия Фишера. Проверяется гипотеза:

H₀: b = b₀ (27)

H₁: b  b₀

Тогда статистика 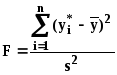имеет распределение ФишераF(1; n - 2). Здесь k₁ = 1 и k₂ = n - 2 - степени свободы распределения.

Если при заданном уровне значимости  критическое значение F_кр(; 1; n - 2) меньше наблюдаемого значения F_набл , то гипотеза Н₀ - отвергается и имеет место зависимость у от х, то есть использование уравнения регрессии улучшает точность прогноза по сравнению с тривиальным: .