Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Алтайский государственный педагогический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

moya_kursovaya1111.docx

Скачиваний:

Добавлен:

18.03.2015

Размер:

220.95 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 76 7 > Следующая >>>

Глава 4.Прогнозирование цены на природный газ

Нам даны ежемесячные цены на природный газ в долларах за 1000 м³ начиная с июля 2009 года заканчивая декабрём 2012.

T	x(t)
1	100,1
2	102,1
3	100,9
4	100,6
5	100,4
6	101,3
7	104,5
8	101,7
9	100,6
10	99,9
11	101
12	101
13	99,3
14	99,9
15	102,5
16	101,2
17	102
18	100,2
19	100,4
20	100
21	99,8
22	100
23	99,8
24	102,8
25	99,8
26	100,6
27	104,2
28	101,6
29	100,5
30	100,7
31	100,5
32	100,4
33	104
34	102,6
35	100,5
36	101,5
37	101,1
38	105,3
39	101,7
40	100
41	100,12
42	101,65

Задача состоит в построении модели, по которой можно сделать достоверный прогноз.

Удаляем 2 последних наблюдения и графически проверяем ряд на наличие сезонности.

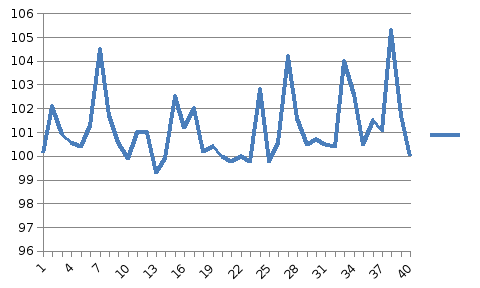
По графику ряда можно установить развитие амплитуды колебания. Это свидетельствует о возможном присутствии аддитивной или мультипликативной модели в ряде.

Построим автокорреляционные функции ACF и PACF. Для этого мы должны нормировать x(t), то есть вычесть из каждой компоненты математическое ожидание, которое равно 101,18.

Затем найдем автоковариационную функцию по формуле:

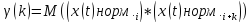
x(t) - норм.	лаг1	лаг2	лаг3	лаг4	лаг5	лаг6	лаг7	лаг8	лаг9	ла10	лаг11	лаг12
-1,08	-0,99	0,30	0,62	0,83	-0,13	-3,57	-0,56	0,62	1,37	0,19	0,19	2,02
0,92	-0,25	-0,53	-0,72	0,12	3,08	0,49	-0,53	-1,18	-0,16	-0,16	-1,73	-1,18
-0,27	0,16	0,21	-0,03	-0,91	-0,14	0,16	0,35	0,05	0,05	0,52	0,35	-0,36
-0,58	0,45	-0,07	-1,91	-0,30	0,33	0,73	0,10	0,10	1,08	0,73	-0,76	-0,01
-0,77	-0,10	-2,58	-0,41	0,45	0,99	0,14	0,14	1,45	0,99	-1,03	-0,02	-0,64
0,13	0,42	0,07	-0,07	-0,16	-0,02	-0,02	-0,23	-0,16	0,17	0,00	0,10	-0,12
3,33	1,75	-1,91	-4,24	-0,58	-0,58	-6,23	-4,24	4,41	0,08	2,74	-3,24	-2,58
0,53	-0,30	-0,67	-0,09	-0,09	-0,98	-0,67	0,70	0,01	0,43	-0,51	-0,41	-0,62
-0,58	0,73	0,10	0,10	1,08	0,73	-0,76	-0,01	-0,47	0,56	0,45	0,68	0,79
-1,27	0,22	0,22	2,39	1,63	-1,69	-0,03	-1,05	1,24	0,99	1,50	1,75	1,50
-0,17	0,03	0,33	0,22	-0,23	0,00	-0,14	0,17	0,14	0,21	0,24	0,21	0,24
-0,17	0,33	0,22	-0,23	0,00	-0,14	0,17	0,14	0,21	0,24	0,21	0,24	-0,28
-1,88	2,39	-2,48	-0,05	-1,55	1,83	1,45	2,20	2,58	2,20	2,58	-3,05	2,58
-1,27	-1,69	-0,03	-1,05	1,24	0,99	1,50	1,75	1,50	1,75	-2,07	1,75	0,73
1,33	0,03	1,09	-1,29	-1,03	-1,56	-1,82	-1,56	-1,82	2,15	-1,82	-0,76	4,01
0,03	0,02	-0,02	-0,02	-0,03	-0,03	-0,03	-0,03	0,04	-0,03	-0,01	0,08	0,01
0,83	-0,80	-0,64	-0,97	-1,13	-0,97	-1,13	1,34	-1,13	-0,47	2,50	0,35	-0,56
-0,97	0,76	1,15	1,34	1,15	1,34	-1,58	1,34	0,56	-2,95	-0,41	0,66	0,46
-0,77	0,91	1,07	0,91	1,07	-1,26	1,07	0,45	-2,34	-0,33	0,52	0,37	0,52
-1,18	1,62	1,38	1,62	-1,91	1,62	0,68	-3,55	-0,50	0,79	0,56	0,79	0,91
-1,38	1,62	1,89	-2,23	1,89	0,79	-4,16	-0,58	0,93	0,65	0,93	1,07	-3,88
-1,18	1,62	-1,91	1,62	0,68	-3,55	-0,50	0,79	0,56	0,79	0,91	-3,32	-1,67
-1,38	-2,23	1,89	0,79	-4,16	-0,58	0,93	0,65	0,93	1,07	-3,88	-1,96	0,93
1,63	-2,23	-0,93	4,92	0,69	-1,10	-0,77	-1,10	-1,26	4,59	2,32	-1,10	0,53
-1,38	0,79	-4,16	-0,58	0,93	0,65	0,93	1,07	-3,88	-1,96	0,93	-0,45	0,10
-0,58	-1,74	-0,24	0,39	0,27	0,39	0,45	-1,62	-0,82	0,39	-0,19	0,04	-2,37
3,03	1,29	-2,04	-1,44	-2,04	-2,34	8,55	4,31	-2,04	0,98	-0,23	12,48	1,59
0,42	-0,29	-0,20	-0,29	-0,33	1,20	0,61	-0,29	0,14	-0,03	1,75	0,22	-0,50
-0,67	0,32	0,46	0,52	-1,91	-0,96	0,46	-0,22	0,05	-2,78	-0,35	0,79
-0,47	0,32	0,37	-1,34	-0,68	0,32	-0,15	0,04	-1,96	-0,25	0,56
-0,67	0,52	-1,91	-0,96	0,46	-0,22	0,05	-2,78	-0,35	0,79
-0,77	-2,19	-1,10	0,52	-0,25	0,06	-3,20	-0,41	0,91
2,83	4,03	-1,91	0,92	-0,21	11,65	1,48	-3,32
1,43	-0,96	0,46	-0,11	5,88	0,75	-1,67
-0,67	-0,22	0,05	-2,78	-0,35	0,79
0,33	-0,02	1,34	0,17	-0,38
-0,08	-0,31	-0,04	0,09
4,13	2,17	-4,85
0,53	-0,62
-1,18

Получаем следующие значения:

Y(1)	Y(2)	Y(3)	Y(4)	Y(5)	Y(6)	Y(7)	Y(8)	Y(9)	Y(10)	Y(11)	Y(12)
0,19	-0,41	-0,10	0,00	0,32	-0,20	-0,20	-0,05	0,43	0,31	0,18	0,08

Разделив автоковариационную функцию на дисперсию x(t), которая равна 1,980384615 получим автокорреляционную функцию.

r(1)=	r(2)=	r(3)=	r(4)=	r(5)=	r(6)=	r(7)=	r(8)=	r(9)=	r(10)=	r(11)=	r(12)=
0,097	-0,208	-0,050	0,001	0,162	-0,099	-0,101	-0,024	0,218	0,159	0,093	0,039

Так как автокорреляционная функция измеряет тесноту связи между членами одного и того же временного ряда, то можно сделать следующие выводы:

Прямая связь существует между парами х_i и х_i₊₁, х_i и х_i₊₄, х_i и х_i₊₅ ,х_i и х_i₊₉, х_i и х_i₊₁₀, х_i и х_i₊₁₁, х_i и х_i_+12
.

Обратная между х_iи х_i₊₂, х_i и х_i₊₃, х_i и х_i₊₆, х_i и х_i₊₇, х_i и х_i₊₈.

Во всех случаях связь очень слабая.

Теперь необходимо вычислить частную автокорреляционную функцию. Для этого необходимо составить корреляционную матрицу. На ее главной диагонали будут расположены единицы, а вне неё значения автокорреляционной функции.

1,00	0,10	-0,21	-0,05	0,00	0,16	-0,10	-0,10	-0,02	0,22	0,16	0,09	0,04
0,10	1,00	0,10	-0,21	-0,05	0,00	0,16	-0,10	-0,10	-0,02	0,22	0,16	0,09
-0,21	0,10	1,00	0,10	-0,21	-0,05	0,00	0,16	-0,10	-0,10	-0,02	0,22	0,16
-0,05	-0,21	0,10	1,00	0,10	-0,21	-0,05	0,00	0,16	-0,10	-0,10	-0,02	0,22
0,00	-0,05	-0,21	0,10	1,00	0,10	-0,21	-0,05	0,00	0,16	-0,10	-0,10	-0,02
0,16	0,00	-0,05	-0,21	0,10	1,00	0,10	-0,21	-0,05	0,00	0,16	-0,10	-0,10
-0,10	0,16	0,00	-0,05	-0,21	0,10	1,00	0,10	-0,21	-0,05	0,00	0,16	-0,10
-0,10	-0,10	0,16	0,00	-0,05	-0,21	0,10	1,00	0,10	-0,21	-0,05	0,00	0,16
-0,02	-0,10	-0,10	0,16	0,00	-0,05	-0,21	0,10	1,00	0,10	-0,21	-0,05	0,00
0,22	-0,02	-0,10	-0,10	0,16	0,00	-0,05	-0,21	0,10	1,00	0,10	-0,21	-0,05
0,16	0,22	-0,02	-0,10	-0,10	0,16	0,00	-0,05	-0,21	0,10	1,00	0,10	-0,21
0,09	0,16	0,22	-0,02	-0,10	-0,10	0,16	0,00	-0,05	-0,21	0,10	1,00	0,10
0,04	0,09	0,16	0,22	-0,02	-0,10	-0,10	0,16	0,00	-0,05	-0,21	0,10	1,00

Рассчитываются значения частной автокорреляционной функции по формуле:

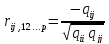
,где q_ij, q_ii, q_jj – алгебраические дополнения элементов r_ij, r_ii, r_jj матрицы выборочных коэффициентов корреляции.

r part(1)=	r part(2)=	r part(3)=	r part(4)=	r part(5)=	r part(6)=	r part(7)=	r part(8)=	r part(9)=	r part(10)=	r part(11)=	r part(12)=
0,097	-0,219	-0,005	-0,040	0,164	-0,158	0,001	-0,070	0,246	0,042	0,240	0,028

Прямая связь существует между парами х_i и х_i₊₁, х_i и х_i₊₅, х_i и х_i₊₇, х_i и х_i₊₉, х_i и х_i₊₁₀, х_i и х_i₊₁₁, х_i и х_i₊₁₂.

Обратная между х_iи х_i₊₂, х_i и х_i₊₃, х_i и х_i₊₄, х_i и х_i₊₆, х_i и х_i₊₈.

Во всех случаях связь очень слабая.

Построим коррелограмму для ACF и PACF.

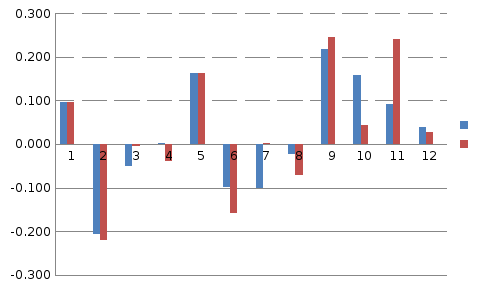
Можно предположить о наличие сезонности с лагом 12.

Теперь рассчитаем компоненты аддитивной модели. Проведем выравнивание данного ряда методом скользящей средней. Для этого просуммируем уровни ряда за каждые 12 месяцев со сдвигом на 1 момент времени. Разделив полученные суммы на 12 найдем скользящие средние. Таким образом мы избавились от сезонной компоненты. Затем найдем центриванные значения скользящей средней.

t	y	скользящая средняя	центрированная скольз. Ср.	x(t) центрир.
1	100,1
2	102,1
3	100,9
4	100,6
5	100,4
6	101,3	101,18
7	104,5	101,11	101,14	3,36
8	101,7	100,93	101,02	0,68
9	100,6	101,06	100,99	-0,39
10	99,9	101,11	101,08	-1,18
11	101	101,24	101,18	-0,17
12	101	101,15	101,20	-0,20
13	99,3	100,81	100,98	-1,68
14	99,9	100,67	100,74	-0,84
15	102,5	100,60	100,63	1,87
16	101,2	100,61	100,60	0,60
17	102	100,51	100,56	1,44
18	100,2	100,66	100,58	-0,38
19	100,4	100,70	100,68	-0,28
20	100	100,76	100,73	-0,73
21	99,8	100,90	100,83	-1,03
22	100	100,93	100,92	-0,92
23	99,8	100,81	100,87	-1,07
24	102,8	100,85	100,83	1,97
25	99,8	100,86	100,85	-1,05
26	100,6	100,89	100,88	-0,28
27	104,2	101,24	101,07	3,13
28	101,6	101,46	101,35	0,25
29	100,5	101,52	101,49	-0,99
30	100,7	101,41	101,46	-0,76
31	100,5	101,52	101,46	-0,96
32	100,4	101,91	101,71	-1,31
33	104	101,70	101,80	2,20
34	102,6	101,57	101,63	0,97
35	100,5
36	101,5
37	101,1
38	105,3
39	101,7
40	100

Используем эти оценки для расчета сезонной компоненты S. Для этого найдем средние за каждый месяц (по всем годам) оценки сезонной компоненты.

Показ	год	янв.	фев	мар	апр	май	июн	июл	авг	сен	окт	ноя	дек
	1							3,36	0,68	-0,39	-1,18	-0,17	-0,20
	2	-1,68	-0,84	1,87	0,60	1,44	-0,38	-0,28	-0,73	-1,03	-0,92	-1,07	1,97
	3	-1,05	-0,28	3,13	0,25	-0,99	-0,76	-0,96	-1,31	2,20	0,97

Определим корректирующий элемент.

Отнимем его от каждой средней. Получим значения сезонных компонент, сумма которых рана 0.

S1=	S2=	S3=	S4=	S5=	S6=	S7=	S8=	S9=	S10=	S11=	S12=
-1,45	-0,64	2,41	0,34	0,14	-0,66	0,62	-0,54	0,17	-0,47	-0,71	0,80

y	S	Y-S	T	E	E^2	(T-Yср)^2
100,1	-1,45	101,5543	100,8247	0,7296	0,5323	0,1116
102,1	-0,64	102,7439	100,8419	1,9020	3,6178	0,1004
100,9	2,41	98,4877	100,8590	-2,3713	5,6232	0,0899
100,6	0,34	100,2648	100,8761	-0,6114	0,3738	0,0799
100,4	0,14	100,2606	100,8933	-0,6327	0,4003	0,0705
101,3	-0,66	101,9606	100,9104	1,0502	1,1029	0,0617
104,5	0,62	103,8821	100,9275	2,9546	8,7296	0,0535
101,7	-0,54	102,2405	100,9447	1,2958	1,6791	0,0458
100,6	0,17	100,4293	100,9618	-0,5324	0,2835	0,0388
99,9	-0,47	100,3655	100,9789	-0,6135	0,3763	0,0323
101	-0,71	101,7106	100,9960	0,7146	0,5106	0,0265
101	0,80	100,2002	101,0132	-0,8130	0,6610	0,0212
99,3	-1,45	100,7543	101,0303	-0,2760	0,0762	0,0165
99,9	-0,64	100,5439	101,0474	-0,5035	0,2535	0,0124
102,5	2,41	100,0877	101,0646	-0,9769	0,9543	0,0089
101,2	0,34	100,8648	101,0817	-0,2169	0,0471	0,0059
102	0,14	101,8606	101,0988	0,7618	0,5803	0,0036
100,2	-0,66	100,8606	101,1159	-0,2554	0,0652	0,0018
100,4	0,62	99,7821	101,1331	-1,3510	1,8251	0,0007
100	-0,54	100,5405	101,1502	-0,6098	0,3718	0,0001
99,8	0,17	99,6293	101,1673	-1,5380	2,3654	0,0001
100	-0,47	100,4655	101,1845	-0,7190	0,5170	0,0007
99,8	-0,71	100,5106	101,2016	-0,6910	0,4775	0,0018
102,8	0,80	102,0002	101,2187	0,7815	0,6107	0,0036
99,8	-1,45	101,2543	101,2358	0,0185	0,0003	0,0059
100,6	-0,64	101,2439	101,2530	-0,0091	0,0001	0,0089
104,2	2,41	101,7877	101,2701	0,5176	0,2679	0,0124
101,6	0,34	101,2648	101,2872	-0,0225	0,0005	0,0165
100,5	0,14	100,3606	101,3044	-0,9438	0,8907	0,0212
100,7	-0,66	101,3606	101,3215	0,0391	0,0015	0,0265
100,5	0,62	99,8821	101,3386	-1,4565	2,1214	0,0323
100,4	-0,54	100,9405	101,3558	-0,4153	0,1725	0,0388
104	0,17	103,8293	101,3729	2,4565	6,0342	0,0458
102,6	-0,47	103,0655	101,3900	1,6754	2,8071	0,0535
100,5	-0,71	101,2106	101,4071	-0,1966	0,0386	0,0617
101,5	0,80	100,7002	101,4243	-0,7241	0,5243	0,0705
101,1	-1,45	102,5543	101,4414	1,1129	1,2386	0,0799
105,3	-0,64	105,9439	101,4585	4,4854	20,1188	0,0899
101,7	2,41	99,2877	101,4757	-2,1880	4,7873	0,1004
100	0,34	99,6648	101,4928	-1,8280	3,3417	0,1116

Выше мы занесли полученные сезонные компоненты в таблицу для соответствующего месяца каждого года.

Элиминируем влияние сезонной компоненты, вычитая ее значение из каждого уровня исходного временного ряда. Получим T+E=x(t)-S. То есть рассчитанные значения включают только тренд и случайную компоненту.

Для того чтобы определить компоненту Т мы провели аналитическое выравнивание ряда (Т+Е) с помощью линейного тренда. Таким образом имеем линейный тренд T= 100,8076175+ 0,01712926*t. подставим в это уравнение значения t и тем самым найдем уровни Т для каждого момента времени. Расчет ошибки проводится по формуле Е=(Т+Е)-Т.

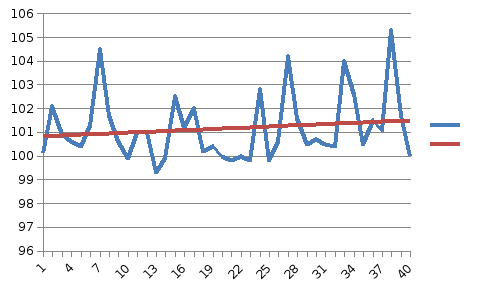
На графике изображен исходный ряд и тренд. По нему видно как мы сгладили ряд.

Для оценки качества рассчитаем ESS (сумма квадратов ошибок), RSS (сумма квадратов разности наблюдаемых значений и средней), TSS=ESS+RSS, R^2=.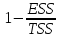

ESS=	RSS=	TSS=	R^2=
74,380	1,564	75,944	0,021

Заметим, так как R^2 достаточно маленький, то модель объясняет только 2,1% общей вариации.

Теперь построим мультипликативную модель. Проводим выравнивание методом скользящей средней также как и в аддитивной модели, только избавляясь от цикличности мы x(t) делим на центрированную скользящую среднюю.

t	y	скользящая средняя	центрированная скольз. Ср.	x(t) центрир.
1	100,1
2	102,1
3	100,9
4	100,6
5	100,4
6	101,3	101,18
7	104,5	101,11	101,14	1,03
8	101,7	100,93	101,02	1,01
9	100,6	101,06	100,99	1,00
10	99,9	101,11	101,08	0,99
11	101	101,24	101,18	1,00
12	101	101,15	101,20	1,00
13	99,3	100,81	100,98	0,98
14	99,9	100,67	100,74	0,99
15	102,5	100,60	100,63	1,02
16	101,2	100,61	100,60	1,01
17	102	100,51	100,56	1,01
18	100,2	100,66	100,58	1,00
19	100,4	100,70	100,68	1,00
20	100	100,76	100,73	0,99
21	99,8	100,90	100,83	0,99
22	100	100,93	100,92	0,99
23	99,8	100,81	100,87	0,99
24	102,8	100,85	100,83	1,02
25	99,8	100,86	100,85	0,99
26	100,6	100,89	100,88	1,00
27	104,2	101,24	101,07	1,03
28	101,6	101,46	101,35	1,00
29	100,5	101,52	101,49	0,99
30	100,7	101,41	101,46	0,99
31	100,5	101,52	101,46	0,99
32	100,4	101,91	101,71	0,99
33	104	101,70	101,80	1,02
34	102,6	101,57	101,63	1,01
35	100,5
36	101,5
37	101,1
38	105,3
39	101,7
40	100

Рассчитаем сезонные компоненты.

показатель	год	янв.	фев	мар	апр	май	июн	июл	авг	сен	окт	ноя	дек
	1							1,03	1,01	1,00	0,99	1,00	1,00
	2	0,98	0,99	1,02	1,01	1,01	1,00	1,00	0,99	0,99	0,99	0,99	1,02
	3	0,99	1,00	1,03	1,00	0,99	0,99	0,99	0,99	1,02	1,01

Сумма средних оценок сезонных компонент равна 12,0104. Рассчитаем корректирующий коэффициент, разделив 12 (месяцев) на сумму средних оценок сезонных компонент. К= 0,999130737.

Умножим его она каждую среднюю. Получим значения сезонных компонент, сумма которых рана 12.

S1=	S2=	S3=	S4=	S5=	S6=	S7=	S8=	S9=	S10=	S11=	S12=
0,99	0,99	1,02	1,00	1,00	0,99	1,01	0,99	1,00	1,00	0,99	1,01

Запишем их в таблицу и рассчитаем остальные компоненты модели.

y	S	Y/S	T	E	E^2	(T-Yср)^2
100,1	0,99	101,5623	100,8283	0,7234	0,5234	0,1125
102,1	0,99	102,7560	100,8455	1,8983	3,6037	0,1012
100,9	1,02	98,5462	100,8627	-2,3718	5,6255	0,0906
100,6	1,00	100,2669	100,8799	-0,6150	0,3782	0,0805
100,4	1,00	100,2564	100,8971	-0,6416	0,4116	0,0711
101,3	0,99	101,9656	100,9143	1,0444	1,0908	0,0622
104,5	1,01	103,8658	100,9315	2,9522	8,7154	0,0539
101,7	0,99	102,2444	100,9487	1,2888	1,6611	0,0462
100,6	1,00	100,4370	100,9659	-0,5298	0,2807	0,0391
99,9	1,00	100,3642	100,9831	-0,6160	0,3794	0,0326
101	0,99	101,7157	101,0003	0,7104	0,5047	0,0267
101	1,01	100,2055	101,0175	-0,8184	0,6698	0,0214
99,3	0,99	100,7506	101,0347	-0,2800	0,0784	0,0166
99,9	0,99	100,5419	101,0519	-0,5067	0,2568	0,0125
102,5	1,02	100,1089	101,0691	-0,9831	0,9665	0,0089
101,2	1,00	100,8650	101,0863	-0,2221	0,0493	0,0060
102	1,00	101,8542	101,1035	0,7517	0,5651	0,0036
100,2	0,99	100,8583	101,1207	-0,2606	0,0679	0,0018
100,4	1,01	99,7906	101,1379	-1,3555	1,8373	0,0007
100	0,99	100,5353	101,1551	-0,6164	0,3800	0,0001
99,8	1,00	99,6383	101,1723	-1,5365	2,3608	0,0001
100	1,00	100,4647	101,1895	-0,7214	0,5205	0,0007
99,8	0,99	100,5072	101,2067	-0,6945	0,4824	0,0018
102,8	1,01	101,9913	101,2239	0,7736	0,5984	0,0036
99,8	0,99	101,2579	101,2411	0,0166	0,0003	0,0060
100,6	0,99	101,2464	101,2583	-0,0118	0,0001	0,0089
104,2	1,02	101,7692	101,2755	0,5056	0,2556	0,0125
101,6	1,00	101,2636	101,2927	-0,0291	0,0008	0,0166
100,5	1,00	100,3563	101,3099	-0,9549	0,9119	0,0214
100,7	0,99	101,3616	101,3271	0,0343	0,0012	0,0267
100,5	1,01	99,8900	101,3443	-1,4631	2,1407	0,0326
100,4	0,99	100,9375	101,3615	-0,4217	0,1779	0,0391
104	1,00	103,8315	101,3787	2,4568	6,0357	0,0462
102,6	1,00	103,0768	101,3959	1,6731	2,7994	0,0539
100,5	0,99	101,2122	101,4131	-0,1995	0,0398	0,0622
101,5	1,01	100,7016	101,4303	-0,7345	0,5394	0,0711
101,1	0,99	102,5769	101,4475	1,1132	1,2392	0,0805
105,3	0,99	105,9766	101,4647	4,4831	20,0985	0,0906
101,7	1,02	99,3276	101,4819	-2,2058	4,8654	0,1012
100	1,00	99,6689	101,4991	-1,8362	3,3717	0,1125

Для того чтобы определить компоненту Т мы провели аналитическое выравнивание ряда (Т+Е) с помощью линейного тренда. Таким образом имеем линейный тренд T= 100,8111022+ 0,01719887*t. подставим в это уравнение значения t и тем самым найдем уровни Т для каждого момента времени. Расчет ошибки проводится по формуле Е=(Т+Е)-Т.

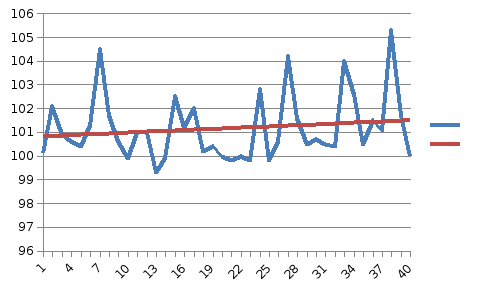
На графике изображен исходный ряд и тренд. По нему видно как мы сгладили ряд.

Для оценки качества рассчитаем ESS, RSS, TSS, R^2.

ESS=	RSS=	TSS=	R^2=
74,485	1,577	76,062	0,021

Теперь необходимо проверить какая из моделей лучше. Для этого проверим их на адекватность с помощью 3-х тестов.

Q-статистика Бокса-Пирса.

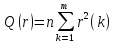–наблюдаемая статистика.

Она имеет асимптотическое распределение хи-квадрат.

Рассчитаем статистику для аддитивной модели.

0,73	0,73	0,53	1,39	-1,73	-0,45	-0,46	0,77	2,16	0,95	-0,39	-0,45	0,52	-0,59	-0,20
1,90	1,90	3,62	-4,51	-1,16	-1,20	2,00	5,62	2,46	-1,01	-1,17	1,36	-1,55	-0,52	-0,96
-2,37	-2,37	5,62	1,45	1,50	-2,49	-7,01	-3,07	1,26	1,45	-1,69	1,93	0,65	1,19	2,32
-0,61	-0,61	0,37	0,39	-0,64	-1,81	-0,79	0,33	0,38	-0,44	0,50	0,17	0,31	0,60	0,13
-0,63	-0,63	0,40	-0,66	-1,87	-0,82	0,34	0,39	-0,45	0,51	0,17	0,32	0,62	0,14	-0,48
1,05	1,05	1,10	3,10	1,36	-0,56	-0,64	0,75	-0,85	-0,29	-0,53	-1,03	-0,23	0,80	-0,27
2,95	2,95	8,73	3,83	-1,57	-1,81	2,11	-2,40	-0,82	-1,49	-2,89	-0,64	2,25	-0,75	-3,99
1,30	1,30	1,68	-0,69	-0,79	0,93	-1,05	-0,36	-0,65	-1,27	-0,28	0,99	-0,33	-1,75	-0,79
-0,53	-0,53	0,28	0,33	-0,38	0,43	0,15	0,27	0,52	0,12	-0,41	0,14	0,72	0,32	0,82
-0,61	-0,61	0,38	-0,44	0,50	0,17	0,31	0,60	0,13	-0,47	0,16	0,83	0,37	0,94	0,44
0,71	0,71	0,51	-0,58	-0,20	-0,36	-0,70	-0,16	0,54	-0,18	-0,97	-0,44	-1,10	-0,51	-0,49
-0,81	-0,81	0,66	0,22	0,41	0,79	0,18	-0,62	0,21	1,10	0,50	1,25	0,58	0,56	-0,64
-0,28	-0,28	0,08	0,14	0,27	0,06	-0,21	0,07	0,37	0,17	0,42	0,20	0,19	-0,22	-0,01
-0,50	-0,50	0,25	0,49	0,11	-0,38	0,13	0,68	0,31	0,77	0,36	0,35	-0,39	-0,01	0,00
-0,98	-0,98	0,95	0,21	-0,74	0,25	1,32	0,60	1,50	0,70	0,68	-0,76	-0,02	0,01	-0,51
-0,22	-0,22	0,05	-0,17	0,06	0,29	0,13	0,33	0,16	0,15	-0,17	0,00	0,00	-0,11	0,00
0,76	0,76	0,58	-0,19	-1,03	-0,46	-1,17	-0,55	-0,53	0,60	0,01	-0,01	0,39	-0,02	-0,72
-0,26	-0,26	0,07	0,34	0,16	0,39	0,18	0,18	-0,20	0,00	0,00	-0,13	0,01	0,24	-0,01
-1,35	-1,35	1,83	0,82	2,08	0,97	0,93	-1,06	-0,02	0,01	-0,70	0,03	1,27	-0,05	1,97
-0,61	-0,61	0,37	0,94	0,44	0,42	-0,48	-0,01	0,01	-0,32	0,01	0,58	-0,02	0,89	0,25
-1,54	-1,54	2,37	1,11	1,06	-1,20	-0,03	0,01	-0,80	0,03	1,45	-0,06	2,24	0,64	-3,78
-0,72	-0,72	0,52	0,50	-0,56	-0,01	0,01	-0,37	0,02	0,68	-0,03	1,05	0,30	-1,77	-1,20
-0,69	-0,69	0,48	-0,54	-0,01	0,01	-0,36	0,02	0,65	-0,03	1,01	0,29	-1,70	-1,16	0,14
0,78	0,78	0,61	0,01	-0,01	0,40	-0,02	-0,74	0,03	-1,14	-0,32	1,92	1,31	-0,15	-0,57
0,02	0,02	0,00	0,00	0,01	0,00	-0,02	0,00	-0,03	-0,01	0,05	0,03	0,00	-0,01	0,02
-0,01	-0,01	0,00	0,00	0,00	0,01	0,00	0,01	0,00	-0,02	-0,02	0,00	0,01	-0,01	-0,04
0,52	0,52	0,27	-0,01	-0,49	0,02	-0,75	-0,21	1,27	0,87	-0,10	-0,37	0,58	2,32	-1,13
-0,02	-0,02	0,00	0,02	0,00	0,03	0,01	-0,06	-0,04	0,00	0,02	-0,03	-0,10	0,05	0,04
-0,94	-0,94	0,89	-0,04	1,37	0,39	-2,32	-1,58	0,19	0,68	-1,05	-4,23	2,06	1,73
0,04	0,04	0,00	-0,06	-0,02	0,10	0,07	-0,01	-0,03	0,04	0,18	-0,09	-0,07
-1,46	-1,46	2,12	0,60	-3,58	-2,44	0,29	1,05	-1,62	-6,53	3,19	2,66
-0,42	-0,42	0,17	-1,02	-0,70	0,08	0,30	-0,46	-1,86	0,91	0,76
2,46	2,46	6,03	4,12	-0,48	-1,78	2,73	11,02	-5,37	-4,49
1,68	1,68	2,81	-0,33	-1,21	1,86	7,52	-3,67	-3,06
-0,20	-0,20	0,04	0,14	-0,22	-0,88	0,43	0,36
-0,72	-0,72	0,52	-0,81	-3,25	1,58	1,32
1,11	1,11	1,24	4,99	-2,44	-2,03
4,49	4,49	20,12	-9,81	-8,20
-2,19	-2,19	4,79	4,00
-1,83	-1,83	3,34

В первой графе мы выписали остатки аддитивной модели. Во второй вычли из первой математическое ожидание ошибки, которое равно -0,000000000000008171. Затем находим (e-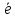)*(e(t-1) -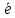), т. е. произведение центрированной ошибки на центрированную ошибку, смещенную на 1 лаг. В следующей графе на 2 лага и т. д. Потом находим математическое ожидание этих произведений, тем самым рассчитав автоковариационную функцию ошибки.

Y(1)	Y(2)	Y(3)	Y(4)	Y(5)	Y(6)	Y(7)	Y(8)	Y(9)	Y(10)	Y(11)	Y(12)
0,24	-0,58	-0,26	0,12	0,22	-0,12	-0,24	-0,04	0,19	0,30	0,10	-0,34

Разделив эти данные на дисперсию, которая равна 1,76569066, получим значения автокорреляционной функции.

r(1)=	r(2)=	r(3)=	r(4)=	r(5)=	r(6)=	r(7)=	r(8)=	r(9)=	r(10)=	r(11)=	r(12)=
0,12	-0,30	-0,13	0,06	0,12	-0,06	-0,13	-0,02	0,10	0,16	0,05	-0,18

Теперь по формуле мы должны возвести эти значения в квадрат, суммировать и умножить на количество наблюдений (115).

Q_набл.= 11,40802528. Q критическое равно ХИ2 с вероятностью 0,05 и степенью свободы 12. Q_кр.=21,02607.

Q_набл.< Q_кр. Следовательно автокорреляция отсутствует на уровне 95%.

Проведем те же самые расчеты для мультипликативной модели.

0,72	0,73	0,53	1,39	-1,72	-0,44	-0,46	0,76	2,15	0,94	-0,38	-0,45	0,52	-0,59	-0,20
1,90	1,90	3,62	-4,50	-1,16	-1,21	2,00	5,63	2,46	-1,00	-1,16	1,36	-1,55	-0,52	-0,95
-2,37	-2,37	5,60	1,44	1,51	-2,48	-7,00	-3,06	1,24	1,45	-1,69	1,93	0,65	1,19	2,32
-0,61	-0,61	0,37	0,39	-0,64	-1,80	-0,79	0,32	0,37	-0,44	0,50	0,17	0,31	0,60	0,13
-0,64	-0,64	0,41	-0,67	-1,88	-0,82	0,33	0,39	-0,46	0,52	0,18	0,32	0,62	0,14	-0,48
1,04	1,05	1,10	3,10	1,36	-0,55	-0,64	0,75	-0,85	-0,29	-0,53	-1,03	-0,23	0,79	-0,27
2,95	2,96	8,74	3,83	-1,55	-1,81	2,12	-2,41	-0,81	-1,48	-2,89	-0,64	2,24	-0,76	-3,99
1,29	1,29	1,67	-0,68	-0,79	0,93	-1,05	-0,36	-0,65	-1,27	-0,28	0,98	-0,33	-1,75	-0,79
-0,53	-0,52	0,28	0,32	-0,38	0,43	0,14	0,26	0,51	0,11	-0,40	0,13	0,71	0,32	0,80
-0,62	-0,61	0,37	-0,44	0,50	0,17	0,31	0,60	0,13	-0,46	0,16	0,83	0,37	0,94	0,44
0,71	0,72	0,51	-0,58	-0,20	-0,36	-0,70	-0,16	0,54	-0,18	-0,97	-0,44	-1,10	-0,51	-0,49
-0,82	-0,81	0,66	0,22	0,41	0,80	0,18	-0,62	0,21	1,10	0,50	1,25	0,58	0,56	-0,63
-0,28	-0,27	0,08	0,14	0,27	0,06	-0,21	0,07	0,37	0,17	0,42	0,20	0,19	-0,21	-0,01
-0,51	-0,50	0,25	0,49	0,11	-0,38	0,13	0,68	0,31	0,77	0,36	0,35	-0,39	-0,01	0,00
-0,98	-0,98	0,96	0,21	-0,74	0,25	1,32	0,60	1,50	0,70	0,67	-0,76	-0,02	0,01	-0,50
-0,22	-0,22	0,05	-0,16	0,06	0,29	0,13	0,33	0,16	0,15	-0,17	0,00	0,00	-0,11	0,01
0,75	0,76	0,57	-0,19	-1,02	-0,46	-1,16	-0,54	-0,52	0,59	0,02	-0,01	0,39	-0,02	-0,72
-0,26	-0,26	0,07	0,35	0,16	0,39	0,18	0,18	-0,20	-0,01	0,00	-0,13	0,01	0,24	-0,01
-1,36	-1,35	1,82	0,83	2,07	0,97	0,93	-1,05	-0,03	0,01	-0,69	0,03	1,28	-0,05	1,97
-0,62	-0,61	0,37	0,94	0,44	0,42	-0,48	-0,01	0,00	-0,31	0,01	0,58	-0,02	0,89	0,25
-1,54	-1,53	2,35	1,10	1,06	-1,19	-0,03	0,01	-0,78	0,04	1,45	-0,06	2,23	0,64	-3,77
-0,72	-0,72	0,51	0,49	-0,56	-0,02	0,00	-0,37	0,02	0,68	-0,03	1,04	0,30	-1,76	-1,20
-0,69	-0,69	0,48	-0,54	-0,01	0,00	-0,35	0,02	0,65	-0,03	1,01	0,29	-1,70	-1,16	0,13
0,77	0,78	0,61	0,02	-0,01	0,40	-0,02	-0,74	0,03	-1,14	-0,32	1,92	1,31	-0,15	-0,57
0,02	0,02	0,00	0,00	0,01	0,00	-0,02	0,00	-0,03	-0,01	0,05	0,04	0,00	-0,02	0,02
-0,01	-0,01	0,00	0,00	0,00	0,01	0,00	0,01	0,00	-0,02	-0,01	0,00	0,00	-0,01	-0,03
0,51	0,51	0,26	-0,01	-0,48	0,02	-0,74	-0,21	1,26	0,86	-0,10	-0,37	0,57	2,29	-1,12
-0,03	-0,02	0,00	0,02	0,00	0,04	0,01	-0,06	-0,04	0,00	0,02	-0,03	-0,11	0,05	0,04
-0,95	-0,95	0,90	-0,04	1,39	0,40	-2,34	-1,59	0,18	0,69	-1,06	-4,26	2,09	1,74
0,03	0,04	0,00	-0,06	-0,02	0,10	0,07	-0,01	-0,03	0,04	0,18	-0,09	-0,07
-1,46	-1,46	2,13	0,61	-3,59	-2,45	0,28	1,06	-1,63	-6,54	3,21	2,67
-0,42	-0,42	0,17	-1,03	-0,70	0,08	0,30	-0,47	-1,87	0,92	0,76
2,46	2,46	6,06	4,13	-0,48	-1,80	2,75	11,05	-5,42	-4,51
1,67	1,68	2,82	-0,33	-1,22	1,88	7,53	-3,69	-3,07
-0,20	-0,19	0,04	0,14	-0,22	-0,87	0,43	0,36
-0,73	-0,73	0,53	-0,82	-3,27	1,61	1,34
1,11	1,12	1,25	5,02	-2,46	-2,05
4,48	4,49	20,14	-9,88	-8,22
-2,21	-2,20	4,84	4,03
-1,84	-1,83	3,35

Y(1)	Y(2)	Y(3)	Y(4)	Y(5)	Y(6)	Y(7)	Y(8)	Y(9)	Y(10)	Y(11)	Y(12)
0,24	-0,58	-0,26	0,12	0,22	-0,13	-0,24	-0,04	0,19	0,30	0,10	-0,34

D(e)= 1,765450423

Автокорреляционная функция.

r(1)=	r(2)=	r(3)=	r(4)=	r(5)=	r(6)=	r(7)=	r(8)=	r(9)=	r(10)=	r(11)-	r(12)=
0,12	-0,30	-0,13	0,07	0,12	-0,07	-0,13	-0,02	0,10	0,15	0,05	-0,18

Q_набл.= 11,3820395.

Q_кр.=21,02607.

Q_набл.< Q_кр. Следовательно автокорреляция отсутствует на уровне 95%.

Вывод: по статистике Бокса-Пирса обе модели равнозначны, автокорреляция в них отсутствует.

2.Тест Дарбина-Уотсона.

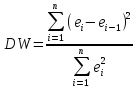–наблюдаемая статистика.

Дарбин и Уотсон доказали, что существует 2 границы d_u и d_l, которые зависят от объема выборки, числа регрессоров и уровня значимости, и обладают следующими свойствами:

4-d_l<DW<4 – автокорреляция есть;
4-d_u<DW<4-d_l – зона не определена;
D_u<DW<4-d_u – автокорреляции нет;
D_l<DW<d_u – зона не определена;
0<DW<d_l - автокорреляция есть;

Для обеих моделей числа d_u и d_l будут одинаковы, так как у них равные объем выборки (40), число регрессоров (2) и уровень значимости (0,05).

d_l=	1,39
d_u=	1,6

Осталось рассчитать наблюдаемую статистику.

Для аддитивной модели:

e_t-1	(et-e_t-1)^2	et^2
-	-	0,532307
0,729593	1,374649	3,617785
1,902048	18,26177	5,623214
-2,37133	3,097438	0,373783
-0,61138	0,000454	0,400276
-0,63267	2,832054	1,102914
1,050197	3,626734	8,729636
2,954596	2,751604	1,679097
1,2958	3,342463	0,283493
-0,53244	0,006564	0,376332
-0,61346	1,76361	0,510583
0,714551	2,333397	0,660961
-0,813	0,288409	0,076153
-0,27596	0,051777	0,253516
-0,5035	0,224088	0,9543
-0,97688	0,57753	0,047058
-0,21693	0,957862	0,580302
0,761775	1,034552	0,065206
-0,25535	1,200343	1,825081
-1,35096	0,549383	0,371797
-0,60975	0,86163	2,365419
-1,53799	0,670731	0,516975
-0,71901	0,000785	0,477481
-0,691	2,168121	0,61067
0,781454	0,582112	0,000342
0,018491	0,000759	8,2E-05
-0,00905	0,277329	0,267875
0,517566	0,29165	0,000505
-0,02248	0,848786	0,890713
-0,94378	0,966035	0,001528
0,039095	2,236824	2,121411
-1,45651	1,084106	0,172476
-0,4153	8,247003	6,034182
2,456457	0,609989	2,807096
1,675439	3,504348	0,038632
-0,19655	0,278305	0,524317
-0,7241	3,374706	1,238636
1,11294	11,37345	20,11876
4,485394	44,53399	4,787279
-2,18799	0,129567	3,341697

Для расчета DW разделим сумму 3-ей графы на сумму 4-ой графы.

DW= 1,710481708.

d_u<DW<4-d_u – автокорреляция отсутствует.

Для мультипликативной модели:

e_t-1	(et-e_t-1)^2	et^2
-	-	0,523359
0,723436	1,380391	3,60368
1,898336	18,2342	5,625511
-2,37182	3,08643	0,378215
-0,61499	0,000707	0,411615
-0,64157	2,842558	1,090805
1,044416	3,639559	8,715361
2,952179	2,766691	1,661113
1,288842	3,307391	0,280669
-0,52978	0,007432	0,379445
-0,61599	1,759357	0,504692
0,710417	2,337335	0,669808
-0,81842	0,289916	0,078388
-0,27998	0,051417	0,256778
-0,50673	0,226956	0,966548
-0,98313	0,579224	0,049312
-0,22206	0,948305	0,565121
0,751745	1,02489	0,067924
-0,26062	1,198685	1,837293
-1,35547	0,546154	0,380005
-0,61645	0,846506	2,360842
-1,5365	0,664356	0,520451
-0,72142	0,000724	0,482354
-0,69452	2,15525	0,598394
0,773559	0,572979	0,000276
0,016606	0,000807	0,000139
-0,0118	0,267655	0,255583
0,505552	0,285891	0,000849
-0,02914	0,857106	0,911904
-0,95494	0,978663	0,001179
0,034338	2,242363	2,140704
-1,46311	1,084475	0,177859
-0,42173	8,285811	6,035745
2,456775	0,614076	2,799416
1,673146	3,50662	0,039781
-0,19945	0,286238	0,539436
-0,73446	3,413826	1,239194
1,113191	11,35649	20,09845
4,48313	44,7413	4,865394
-2,20576	0,136571	3,37166

Для расчета DW разделим сумму 3-ей графы на сумму 4-ой графы.

DW= 1,710682171.

d_u<DW<4-d_u – автокорреляция отсутствует.

Вывод: по тесту Дарбина-Уотсона обе модели равнозначны, автокорреляция в них отсутствует.

3.Тест Бреуша-Годфри.

Для расчета наблюдаемой статистики мы должны задать уравнение e(t)=ϒ₁*e(t-1) + ϒ₂*e(t-2) + ϒ₃*e(t-3) + ϒ₄*e(t-4). И найти его R^2.

LM=n*R^2. Где n -количество наблюдений.

Для аддитивной модели:

e(t)	e(t-1)	e(t-2)	e(t-3)	e(t-4)	eнабл.	E(e)	(eнабл-e ср)^2
0,73	-	-	-	-	-	-	-
1,90	0,73	-	-	-	-	-	-
-2,37	1,90	0,73	-	-	-	-	-
-0,61	-2,37	1,90	0,73	-	-	-	-
-0,63	-0,61	-2,37	1,90	0,73	0,53	1,35	0,28
1,05	-0,63	-0,61	-2,37	1,90	0,34	0,51	0,11
2,95	1,05	-0,63	-0,61	-2,37	0,29	7,08	0,09
1,30	2,95	1,05	-0,63	-0,61	0,31	0,96	0,10
-0,53	1,30	2,95	1,05	-0,63	-0,74	0,04	0,55
-0,61	-0,53	1,30	2,95	1,05	-0,63	0,00	0,40
0,71	-0,61	-0,53	1,30	2,95	0,16	0,31	0,03
-0,81	0,71	-0,61	-0,53	1,30	0,47	1,65	0,22
-0,28	-0,81	0,71	-0,61	-0,53	-0,40	0,01	0,16
-0,50	-0,28	-0,81	0,71	-0,61	0,10	0,37	0,01
-0,98	-0,50	-0,28	-0,81	0,71	0,08	1,11	0,01
-0,22	-0,98	-0,50	-0,28	-0,81	-0,10	0,01	0,01
0,76	-0,22	-0,98	-0,50	-0,28	0,27	0,24	0,07
-0,26	0,76	-0,22	-0,98	-0,50	0,26	0,26	0,07
-1,35	-0,26	0,76	-0,22	-0,98	-0,35	1,01	0,12
-0,61	-1,35	-0,26	0,76	-0,22	-0,28	0,11	0,08
-1,54	-0,61	-1,35	-0,26	0,76	0,36	3,59	0,13
-0,72	-1,54	-0,61	-1,35	-0,26	-0,08	0,41	0,01
-0,69	-0,72	-1,54	-0,61	-1,35	0,26	0,91	0,07
0,78	-0,69	-0,72	-1,54	-0,61	0,13	0,43	0,02
0,02	0,78	-0,69	-0,72	-1,54	0,32	0,09	0,10
-0,01	0,02	0,78	-0,69	-0,72	-0,24	0,06	0,06
0,52	-0,01	0,02	0,78	-0,69	-0,11	0,39	0,01
-0,02	0,52	-0,01	0,02	0,78	0,17	0,04	0,03
-0,94	-0,02	0,52	-0,01	0,02	-0,16	0,61	0,03
0,04	-0,94	-0,02	0,52	-0,01	-0,23	0,07	0,05
-1,46	0,04	-0,94	-0,02	0,52	0,34	3,22	0,11
-0,42	-1,46	0,04	-0,94	-0,02	-0,27	0,02	0,07
2,46	-0,42	-1,46	0,04	-0,94	0,29	4,69	0,08
1,68	2,46	-0,42	-1,46	0,04	0,76	0,84	0,58
-0,20	1,68	2,46	-0,42	-1,46	-0,47	0,08	0,22
-0,72	-0,20	1,68	2,46	-0,42	-0,75	0,00	0,56
1,11	-0,72	-0,20	1,68	2,46	-0,03	1,30	0,00
4,49	1,11	-0,72	-0,20	1,68	0,60	15,11	0,36
-2,19	4,49	1,11	-0,72	-0,20	0,66	8,13	0,44
-1,83	-2,19	4,49	1,11	-0,72	-1,99	0,02	3,94

Мы взяли ошибки и сдвинули на 4 лага. Построили по этим данным уравнение регрессии, коэффициенты которого соответственно равны

Y(1)	Y(2)	Y(3)	Y(4)
0,217	-0,309	-0,064	0,071

Нашли наблюдаемые значения, и, вычитая их из реальных, нашли ошибку модели и возвели ее в квадрат.

R^2= 0,142853789

LM_набл.= 5,714151576.

LM_кр. = хи^2(0,05;4)=9,4877.

LM_набл< LM_кр . следовательно автокорреляция отсутствует.

Для мультипликативной модели:

e(t)	e(t-1)	e(t-2)	e(t-3)	e(t-4)	eнабл.	E(e)	(eнабл-e ср)^2
0,72	-	-	-	-	-	-	-
1,90	0,72	-	-	-	-	-	-
-2,37	1,90	0,72	-	-	-	-	-
-0,61	-2,37	1,90	0,72	-	-	-	-
-0,64	-0,61	-2,37	1,90	0,72	0,53	1,38	0,29
1,04	-0,64	-0,61	-2,37	1,90	0,34	0,50	0,12
2,95	1,04	-0,64	-0,61	-2,37	0,29	7,07	0,09
1,29	2,95	1,04	-0,64	-0,61	0,31	0,95	0,10
-0,53	1,29	2,95	1,04	-0,64	-0,75	0,05	0,55
-0,62	-0,53	1,29	2,95	1,04	-0,63	0,00	0,39
0,71	-0,62	-0,53	1,29	2,95	0,16	0,30	0,03
-0,82	0,71	-0,62	-0,53	1,29	0,47	1,66	0,23
-0,28	-0,82	0,71	-0,62	-0,53	-0,40	0,01	0,15
-0,51	-0,28	-0,82	0,71	-0,62	0,10	0,37	0,01
-0,98	-0,51	-0,28	-0,82	0,71	0,08	1,13	0,01
-0,22	-0,98	-0,51	-0,28	-0,82	-0,10	0,02	0,01
0,75	-0,22	-0,98	-0,51	-0,28	0,27	0,23	0,07
-0,26	0,75	-0,22	-0,98	-0,51	0,26	0,27	0,07
-1,36	-0,26	0,75	-0,22	-0,98	-0,35	1,02	0,12
-0,62	-1,36	-0,26	0,75	-0,22	-0,28	0,12	0,07
-1,54	-0,62	-1,36	-0,26	0,75	0,36	3,59	0,13
-0,72	-1,54	-0,62	-1,36	-0,26	-0,08	0,42	0,00
-0,69	-0,72	-1,54	-0,62	-1,36	0,26	0,91	0,07
0,77	-0,69	-0,72	-1,54	-0,62	0,13	0,42	0,02
0,02	0,77	-0,69	-0,72	-1,54	0,32	0,09	0,10
-0,01	0,02	0,77	-0,69	-0,72	-0,24	0,05	0,06
0,51	-0,01	0,02	0,77	-0,69	-0,11	0,37	0,01
-0,03	0,51	-0,01	0,02	0,77	0,17	0,04	0,03
-0,95	-0,03	0,51	-0,01	0,02	-0,16	0,63	0,02
0,03	-0,95	-0,03	0,51	-0,01	-0,23	0,07	0,05
-1,46	0,03	-0,95	-0,03	0,51	0,34	3,26	0,12
-0,42	-1,46	0,03	-0,95	-0,03	-0,27	0,02	0,07
2,46	-0,42	-1,46	0,03	-0,95	0,29	4,69	0,09
1,67	2,46	-0,42	-1,46	0,03	0,76	0,84	0,58
-0,20	1,67	2,46	-0,42	-1,46	-0,48	0,08	0,22
-0,73	-0,20	1,67	2,46	-0,42	-0,75	0,00	0,55
1,11	-0,73	-0,20	1,67	2,46	-0,03	1,30	0,00
4,48	1,11	-0,73	-0,20	1,67	0,60	15,06	0,37
-2,21	4,48	1,11	-0,73	-0,20	0,66	8,21	0,44
-1,84	-2,21	4,48	1,11	-0,73	-1,99	0,02	3,95

Y(1)	Y(2)	Y(3)	Y(4)
0,217	-0,310	-0,063	0,072

R^2= 0,142958371

LM_набл.= 5,718334826.

LM_кр. = хи^2(0,05;4)=9,4877.

LM_набл< LM_кр . следовательно автокорреляция отсутствует.

Вывод: по тесту Бреуша-Годфри обе модели равнозначны, автокорреляции нет.

4.Проведем тест на нормальность по методу Жарге-Бера.

Этот тест выглядит следующим образом. он вычисляет выборочные значения для коэффициентов асимметрии 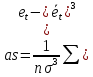и эксцесса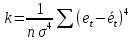, где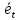– выборочное среднее, аσ – выборочное среднеквадратическое остатков.

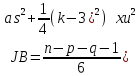
Для адитивной модели:

σ=	1,381005468
σ^3=	2,633820625
σ^4=	3,637320685
AS=	0,997753655
k=	4,316756566
JB=	9,05017069
ХИ=	5,991464547

Остатки распределены не нормально.

Для мультипликативной модели:

σ=	1,38197418
σ^3=	2,639367029
σ^4=	3,647537085
AS=	0,997884135
k=	4,318216536
JB=	9,057910884
ХИ=	5,991464547

Остатки распределены не нормально.

Так как 4 предыдущие статистики не показали какая из моделей лучше, то критериями Акойта и Шварца. Согласно им среди альтернативных гипотез выбираем модель, у которой минимальны следующие величины:

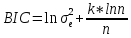
, где n- количество наблюдений, а k-количество регрессоров.

Для аддитивной модели:

D(e)=	1,907176102
AIC=	0,745623668
BIC=	0,83006764

Для мультипликативной модели:

D(e)=	1,909852634
AIC=	0,747026084
BIC=	0,831470057

Вывод: адитивная модель лучше.

Следующим шагом необходимо сделать точечный и интервальный прогноз на 2 шага вперед. Но так как мы в начале удалили 2 последних наблюдения, то у нас есть возможность проверить правильность прогноза.

Рассчитываем точечный прогноз на 41 и 42 период.

X(t)= 100,8076175- 0,01712926*t.

Для точечного прогноза на 41 период в уравнение вместо t подставляем 41. Для 42 периода прогноз делается аналогично.

t	y
41	101,5099
42	101,527

Теперь рассчитаем интервальный прогноз дл я116 периода.

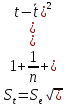
=101,5099; - точечный прогноз.

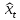+S₁₁ = 100,80; - точечный прогноз + сезонная компонента.

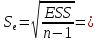1,381005468; - среднеквадратическое отклонение ошибки.

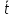= 20,5; - математическое ожидание t.

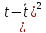= 420,3;

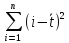=5330;

S_t=1,450940731;

t(1-α;n-2)=t(0,05;38)=2,024394147;

97,862051 <xt< 103,7366028 -интервальный прогноз.

Аналогично проделаем для 42 периода.

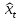=101,527; - точечный прогноз.

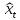+S₁₂ = 102,33; - точечный прогноз + сезонная компонента.

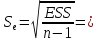1,363633638; - среднеквадратическое отклонение ошибки.

= 21; - математическое ожидание t.

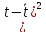=441;

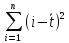=5740;

S_t=1,430983595;

t(1-α;n-2)=t(0,05;39)=2,022690901;

99,43243535<xt< 105,2213103; -интервальный прогноз.

Для проверки правильности прогноза рассчитаем абсолютную и относительную ошибку.

предсказанные значения	реальные значения	интервал	t
100,80	100,12	97,862051<xt<103,7366028	41
102,33	101,65	99,43243535<xt<105,2213103	42

Абсолютная погрешность (предсказанные – реальные):

погрешность	t
0,68	41
0,68	42

Относительная погрешность(предсказанные/ абсолютная погрешность):

погрешность	t
0,67%	41
0,66%	42

Заметим так же, что предсказанные и реальные значения попали в интервальные прогнозы.

<<< < Предыдущая 1 2 3 4 56 / 76 7 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
18.03.2015123.9 Кб36MALKOVA_O.doc
#
18.03.2015539.9 Кб44Mat2_Reky.pdf
#
29.08.2019383.49 Кб20metodicheskie-ukazaniya-k-seminaram.doc
#
18.03.2015302.4 Кб31milov.pdf
#
12.11.2019381.44 Кб15Moro_M_I.doc
#
18.03.2015220.95 Кб47moya_kursovaya1111.docx
#
06.03.201644.05 Кб182Moy_diplomchik.docx
#
06.03.2016237.17 Кб73moy_otchetkontroler.docx
#
06.03.2016162.82 Кб27M_3_P_Pedagogicheskaya_praktika.doc
#
17.07.20193.33 Mб18napoleon.rtf
#
28.09.201963.16 Кб19Na_pechat_otchet_2_-_kopia.docx