
4Практическое занятие 3
Ранг. Решение систем линейных уравнений
Задания:
3.1. Вычислить ранг матрицы:
1)
 ; 2)
; 2)
 .
.
Ответ: 1) 2; 2) 2.
3.2.
1)
 ; 2)
; 2)
 ;
;
3)
 ; 4)
; 4)
 .
.
Ответ: 1) 2; 2) 3; 3) 3; 4) 2.
3.3.
1)
 ; 2)
; 2)
 ;
;
3)
 ; 4)
; 4)
 .
.
Ответ: 1) 2; 2) 3; 3) 5; 4) 4.
3.4.
Зная основную матрицу
![]() и расширенную матрицу
и расширенную матрицу
![]() записать соответствующую им систему
линейных алгебраических уравнений и
решить вопрос о ее совместности или
несовместности, пользуясь теоремой
Кронекера-Капелли:
записать соответствующую им систему
линейных алгебраических уравнений и
решить вопрос о ее совместности или
несовместности, пользуясь теоремой
Кронекера-Капелли:
1)
 ;
;
2)
 .
.
Ответ:
1)
![]() ,
система несовместна
,
система несовместна
![]() ;
;
2)
![]() ,
т.е. система совместна.
,
т.е. система совместна.
3.5. Доказать совместность систем с помощью теоремы Кронекера-Капелли, записать системы в матричной форме и решить их матричным способом:
1)
 2)
2)

Ответ:
1)
![]() ; 2)
; 2)
![]() .
.
3.6. Решить системы уравнений, используя формулы Крамера:
1)
 2)
2)

Ответ:
1)
![]() ;
;
2)
![]() .
.
3.7. Следующие системы решить по правилу Крамера:
1)
 2)
2)

3)
 4)
4)
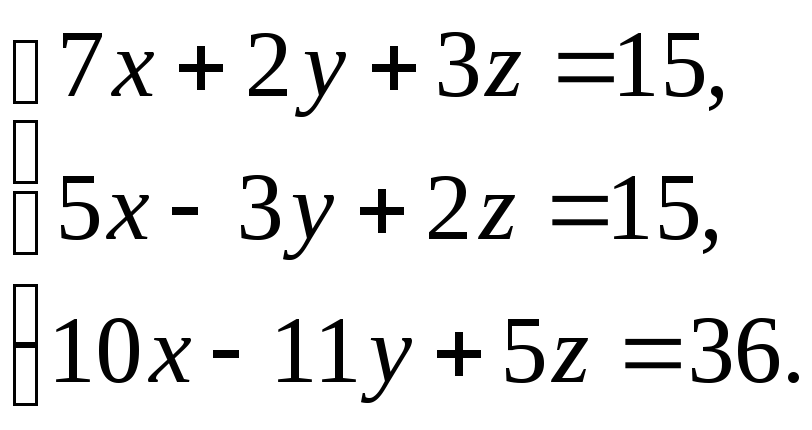
5)
 6)
6)

7)
 8)
8)

Ответ:
1)
![]() ; 2)
; 2)
![]() ;
;
3)
![]() ;
4)
;
4)
![]() ;
;
5)
![]() ; 6)
; 6)
![]() ;
;
7)
![]() ;
;
8)
![]() .
.
3.8. Исследовать совместность и найти общее решение следующих систем:
1)
 2)
2)

3)
 4)
4)

5)
 6)
6)

7)
 8)
8)
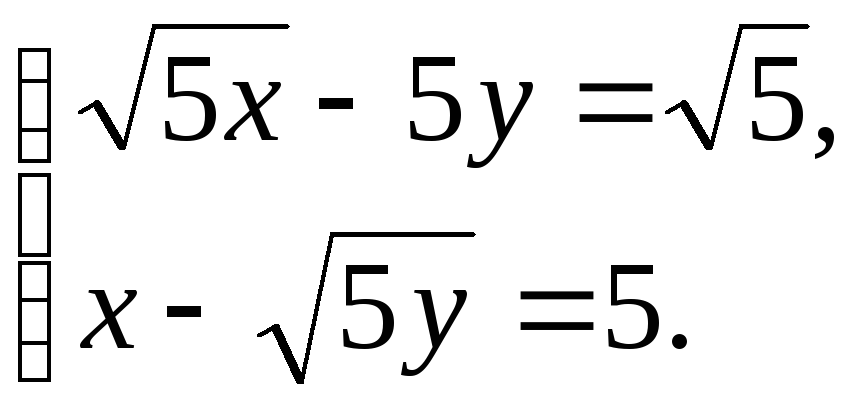
9)
 10)
10)

11)
 12)
12)

13)
 14)
14)

15)
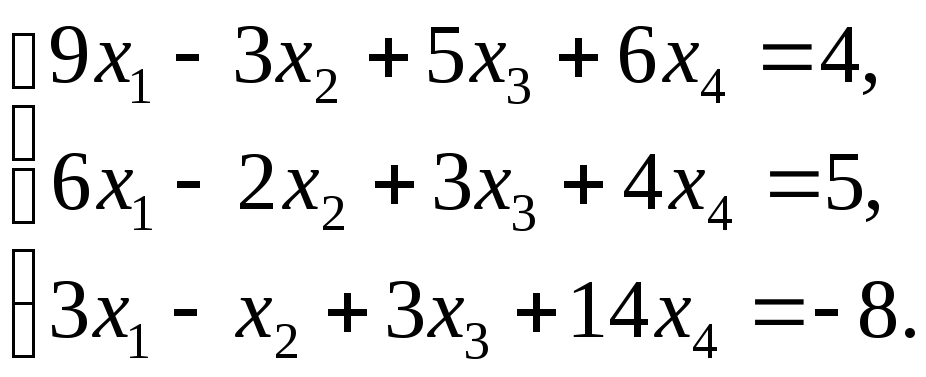 16)
16)

17)

18)

19)

Правильность ответов проверить подстановкой их в исходную систему уравнений.
3.9. Решить системы методом Жордана-Гаусса:
1)
 2)
2)

3)
 4)
4)

Ответ:
1)
![]() (
(![]() любое число);
любое число);
2)
![]()
(![]() любое число);
любое число);
3)
![]() ;
;
4)
![]() .
.
3.10. Найти фундаментальную систему решений и общее решение следующих систем:
1)
 2)
2)
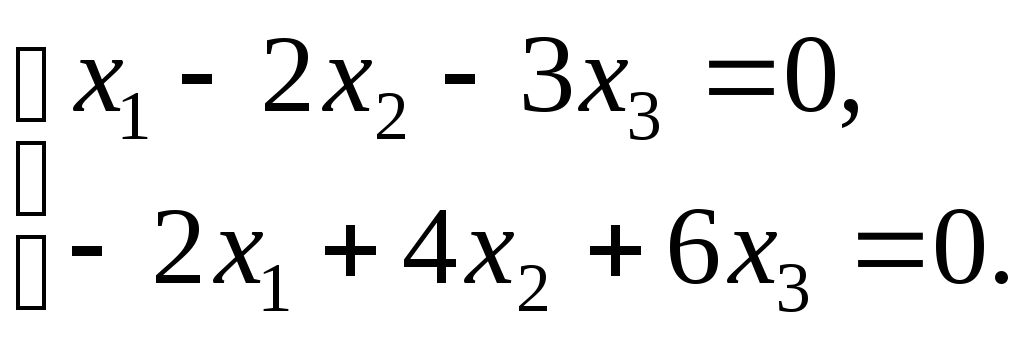
3)
 4)
4)

5)
 6)
6)

7)

8)
 9)
9)

10)

Ответы:
1)
![]() ;
;
2)
![]() ;
;
3) система имеет тривиальное решение;
4)
![]() ;
;
5)
![]() ;
;
6)
![]() ;
;
7)

8)
![]()
9)
![]() ;
;
10)
![]() .
.
3.11. Найти общие решения неоднородных систем, используя фундаментальную систему решений соответствующих однородных:
1)

2)

3)

4)

Ответы:
1)
![]()
![]() ;
;
2)
![]()
![]() ;
;
3)
![]()
![]() ;
;
4)
![]()
![]() .
.
Дополнительные сведения
1.
Ранг матрицы.
Пусть в
матрице
![]() размера
размера
![]() выбраны произвольно
выбраны произвольно
![]() строк и
строк и
![]() столбцов
столбцов
![]() .
Элементы, стоящие на пересечении
выбранных строк и столбцов, образуют
квадратную матрицу порядка
.
Элементы, стоящие на пересечении
выбранных строк и столбцов, образуют
квадратную матрицу порядка
![]() ,
определитель которой называется минором
,
определитель которой называется минором
![]() -го
порядка
матрицы
-го
порядка
матрицы
![]() .
.
Максимальный
порядок
![]() отличных от нуля миноров матрицы
отличных от нуля миноров матрицы
![]() называется ее рангом,
а любой минор порядка
называется ее рангом,
а любой минор порядка
![]() ,
отличный от нуля – базисным
минором.
,
отличный от нуля – базисным
минором.
Строки (столбцы)
матрицы
![]() размера
размера
![]() можно рассматривать как систему
арифметических векторов из
можно рассматривать как систему
арифметических векторов из
![]() (соответственно
(соответственно
![]() ).
).
Теорема о базисном миноре. Ранг матрицы равен рангу системы ее строк (столбцов); при этом система строк (столбцов) матрицы, содержащая базисный минор, образует базис в системе всех строк (столбцов) этой матрицы.
Приведем основные методы вычисления ранга матрицы.
Метод
окаймляющих миноров.
Пусть в матрице найден минор
![]() -го
порядка
-го
порядка
![]() ,
отличный от нуля. Рассмотрим лишь те
миноры
,
отличный от нуля. Рассмотрим лишь те
миноры
![]() -го
порядка, которые содержат в себе
(окаймляют) минор
-го
порядка, которые содержат в себе
(окаймляют) минор
![]() :
если все они равны нулю, то ранг матрицы
равен
:
если все они равны нулю, то ранг матрицы
равен
![]() .
В противном случае среди окаймляющих
миноров найдется ненулевой минор
.
В противном случае среди окаймляющих
миноров найдется ненулевой минор
![]() -го
порядка, и вся процедура повторяется.
-го
порядка, и вся процедура повторяется.
Пример 1. Найти ранг матрицы
 .
.
Фиксируем минор 2-го порядка, отличный от нуля:
![]() .
.
Минор 3-го порядка
 ,
,
Окаймляющий минор
![]() ,
также отличен от нуля. Однако оба минора
4-го порядка, окаймляющие
,
также отличен от нуля. Однако оба минора
4-го порядка, окаймляющие
![]() ,
равны нулю:
,
равны нулю:

Поэтому ранг
![]() равен трем, а базисным минором является,
например,
равен трем, а базисным минором является,
например,
![]() .
.
Метод
элементарных преобразований
основан на том факте, что элементарные
преобразования матрицы не меняют ее
ранга. Используя эти преобразования,
матрицу можно привести к такому виду,
когда все ее элементы, кроме
![]() ,
равны нулю. Следовательно, ранг матрицы
равен
,
равны нулю. Следовательно, ранг матрицы
равен
![]() .
.
Пример 2. Найти ранг матрицы
 .
.
Производя последовательно элементарные преобразования, будем иметь

 .
.
Ранг последней матрицы равен двум, следовательно, таков же и ранг исходной матрицы.
