Интегрирование аппроксимируемой функции
Была выбрана функция, аппроксимирующая с помощью решения СЛАУ методом Крамера.
Аналитический вид функции (полином 3-ей степени):
Вычислим интеграл при помощи стандартных методов MatchCad:
Вычислим значение интеграла при помощи метода центральных (средних) прямоугольников (код программы приведен в Приложении):
Необходимая точность абсолютной погрешности достигается при количестве итераций m = 8.
Значения абсолютной и относительной погрешностей:
Результат, полученный при вычислении интеграла интерполированной функции методом центральных прямоугольников, получен с заданной точностью. При увеличении точности абсолютной погрешности на порядок, количество необходимых итераций возрастает почти в 3 раза, что говорит о чувствительности метода к требуемой точности вычислений.
ВЫЧИСЛЕНИЕ ЗНАЧЕНИЯ ПРОИЗВОДНОЙ ФУНКЦИИ В ТОЧКЕ Х0 = 2.9999
Найдем значение производной аппроксимирующей с помощью решения СЛАУ функции при помощи стандартных средств MathCad:
Построим график полученной функции:
Рисунок 13. График первой производной по аналитической функции, полученный при помощи стандартных средств MathCad.
Найдем приближенное значение первой производной функции, заданной таблично, в указанных точках, используя правое, левое и центральное разностные отношения.
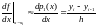- левое разностное отношение
- правое разностное отношение
- центральное разностное отношение
Экспериментальным путем был подобран оптимальный шаг дифференцирования N = 11, при котором достигается минимальная абсолютная и относительная погрешность.
Получим вектор значений:
Построим график полученной функции:
Рисунок 14. График первой производной по таблично заданной функции.
Сравним полученные графики:
Рисунок 15. Сравнение графиков первой производной по таблично заданной функции и функции, заданной аналитически (интерполирование решением СЛАУ).
Формулы для нахождения абсолютной и относительной погрешностей:
Максимальная и минимальная абсолютная погрешность:
Максимальная и минимальная относительная погрешность:
Найдем значение производной, найденной по формуле интерполируемой при помощи решения СЛАУ функции, в точке x0 = 2.9999:
Найдем значение производной, найденной по таблично заданной функции, в точке x0 = 2.9999:
Оценим абсолютную и относительную погрешности для двух полученных значений:
Как видно из полученных значений, в заданной точке х0 погрешность достаточно велика. Однако из рисунка 15 видно, что характер полученных производных совпадает, но имеется сдвиг по оси ОУ. Полученный сдвиг можно объяснить погрешностью исходных данных, а также тем, что при интерполировании таблично заданной функции методом решения СЛАУ, погрешность может накапливаться. В данной ситуации сложно оценить, какая из полученных производных точнее, зато мы можем однозначно утверждать, какого вида должна быть производная первого порядка.
ЗАКЛЮЧЕНИЕ
В ходе проведенной работы была выполнена аппроксимация функции, заданной четырьмя узлами сетки, с использованием различных методов: решения СЛАУ, метода Лагранжа, метода Ньютона, интерполирования сплайнами и аппроксимации полиномами методом наименьших квадратов. Результаты аппроксимации показали, что наилучшие характеристики функции демонстрируют методы полиномиальной аппроксимации, метод Ньютона и интерполирование кубическим сплайном.
Была проведена экстраполяция на два шага вперед, результаты которой позволили сделать выводы о будущем поведении функции. Линейный сплайн показал наилучшие результаты экстраполяции, в то время как другие методы продемонстрировали необоснованный экспоненциальный рост при прогнозировании.
На основе аналитической функции, полученной с использованием метода Крамера для решения СЛАУ, был вычислен интеграл на отрезке [0,3] с заданной точностью ε ≤ 0.01 и ε ≤ 0.001 для абсолютной погрешности, что дало ожидаемые результаты.
Кроме того, были построены графики первой производной, полученные по таблично заданной функции и аналитически, что подтвердило правильность вычислений. Однако наблюдался сдвиг по оси Y, что может быть связано с накоплением погрешностей в процессе интерполяции. В результате было найдено значение производной в точке x0 = 2.9999, которое существенно отличалось из-за сдвига по оси Y для обоих случаев.
СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ
Воскобойников Ю. Е., Задорожный А. Ф. Основы вычислений и программирования в пакете MathCAD PRIME: Учебное пособие. — СПб.: Издательство «Лань», 2016. — 224 с.: ил. — (Учебники для вузов. Специальная литература).
Кирьянов Д. В. Mathcad 15/Mathcad Prime 1.0. — СПб.: БХВ-Петербург, 2012 — 432 с.: ил.
Решение задач вычислительной математики с использованием языка программирования пакета MathCad : учеб. пособие / Г.В. Трошина – Новосибирск: Изд-во НГТУ, 2009 – 86 с.
ПРИЛОЖЕНИЕ
Решение СЛАУ методом Крамера
Программа вычисления интеграла методом центральных прямоугольников
Программа для нахождения вектора значений при интерполяции методом Ньютона
