Лекция 16.

МЕХАНИЧЕСКИЕ И ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ.

16.1. Гармонические колебания и их характеристики

Колебаниями называются процессы, отличающиеся той или иной степенью повторяемости. В зависимости от физической природы повторяющегося процесса различают колебания: механи­ческие, электромагнитные, электромеханические и т.д.. Колебания относятся к процессам, повторяющимся через одинаковые промежутки времени. Например, при механических колебаниях повторяются изменения положе­ний и скоростей тел. Электрические колебания - это повторяющиеся изменения напряжений и силы токов. Несмотря на разную физическую природу, в колебаниях обнаруживаются одни и те же закономерности, которые исследуются общими методами.

Простейшие колебания - это гармонические, т.е. происходящие по закону синуса (или косинуса). Их совершает, например, груз, подвешенный на невесомой пружине (рис.16.1). Его движение можно свести к движению центра масс груза, т.е. одной материальной точки. В этом случае х – смещение точки от положения равновесия.

Величина смещения в любой момент времени t определяется соотношением:

(16.1)

Рис. 16.1

Формула (16.1) называется уравнением гармонического колебания, где А - амплитуда, - циклическая частота, - фаза колебания. Фаза показывает какая доля периода прошла от начала момента колебания.

Рассмотрим скорость, ускорение и энергию точки, совершающей гармонические колебания. Так как , то

, отсюда

, т.е.

(16.2)

Известно F=ma, отсюда c учетом формулы (колебания, происходящие под действием такой силы - гармонические)

Получим (16.3)

Выведем формулу кинетической энергии:

;

Потенциальная по формуле

;

Тогда полная энергия :

(16.4)

16.2 Физический и математический маятники

Известно F= - кx, Обычно F - упругая сила, но если она удовлетворяет условию , то любая сила называется квазиупругой и вызывает гармонические колебания. Если , то можно записать: или , т.е.

(16.5)

при обозначении . Систему, описываемую уравнением (16.5), называют гармоническим осциллятором. Уравнение (16.5) имеет решение в виде . Колебания осциллятора служат моделью во многих физических задачах. Рассмотрим физический маятник.

Физическим маятником называется твердое тело, способное совершать колебания под действием силы тяжести вокруг горизонтальной оси 0, не проходящей через его центр инерции. В положении равновесия центр инерции маятника С находится на одной вертикали с точкой подвеса 0 (рис. 16.2).

Отклоним маятник на малый угол . Составляющая силы тяжести стремится возвратить маятник в положение равновесия Она направлена в сторону убыва­ния угла и равна

Обозначив момент инерции маятника относительно оси буквой , можно написать уравнение движения:

После преобразования уравнение движения примет вид

, где

Учитывая выражение для круговой частоты, получим формулу периода колебаний физического маятника

Рис 16.2 (16.6)

Если вместо физического маятника взять материальную точку, то и период для маятника, состоящего из материальной точки, подвешенной на тонкой, невесомой нерастяжимой нити, определяется

(16.7)

Такой маятник называется математическим.

Из уравнений (16.6) и (16.7) можно получить

(16.8)

т.е. приведенную длину физического маятника. Это длина такого математического маятника, период колебаний которого совпадает с периодом колебаний данного физического маятника.

Колебания маятников - это свободные механические колебания. Рассмотрим свободные электромагнитные колебания.

Электрические колебания могут возникать в цепи, содержащей индуктивность и емкость С, поэтому такая цепь называется колебательным контуром (рис. 16.3).

И

Рис 16.3

звестно, что в таком контуре возникающие электрические колебания сопровождаются взаимными превращениями энергии электрического и магнитного полей , где q - заряд, а i - величина электрического тока.

Во время колебания внешнее напряжение к контуру не приложено. Поэтому сумма падения напряжения на емкости и индуктивности

должна быть равна нулю . Заменив через , получим

, или при (16.9)

Решением этого дифференциального уравнения является функция, описывающая гармонические колебания , где - частота собственных электрических колебаний, а - период этих колебаний.

16.3. Сложение гармонических колебаний

Сложение колебаний облегчается, если колебание представить в виде вектора амплитуды (рис. 16.4). Вектор в момент времени t, составляет угол с осью х. При вращении с постоянной скоростью его проекция на ось х будет совершать гармонические колебания относительно точки 0, т.к. .

Рис. 16.4 Рассмотрим сложение колебаний с одинаковым периодом и одинаковой угловой частотой, но с различными начальными фазами и амплитудами:

Представим колебания векторами и и по правилам сложения векторов построим результирующий вектор (рис. 16.5). Из рисунка следует, и , т.е.

(16.10)

Начальная фаза результирующего колебания также определяется из рисунка

Рис 16.5 Рис 16.6

(16.11)

Получен результирующий вектор колебаний и его начальная фаза.

Если складываются два гармонических колебания, одинаково направленных и их частоты мало отличаются друг от друга, то в результате получается колебание, амплитуда которого периодически изменяется от 0 до максимума и вновь до 0. Такое колебание называется биением (рис. 16.6).

При сложении двух взаимно-перпендикулярных колебаний, такой случай на практике можно получить при колебании груза, удерживаемого двумя пружинами под прямым углом друг к другу (рис. 16.7), смещение пружин изменяется по закону

Рис. 16.7

и

После соответствующих преобразований уравнение траектории движения будет иметь вид

(16.12)

Уравнение (16.12) является уравнением эллипса, оси которого ориентированы относительно координатных осей Х и У произвольно.

Рассмотрим частные случаи этого уравнения.

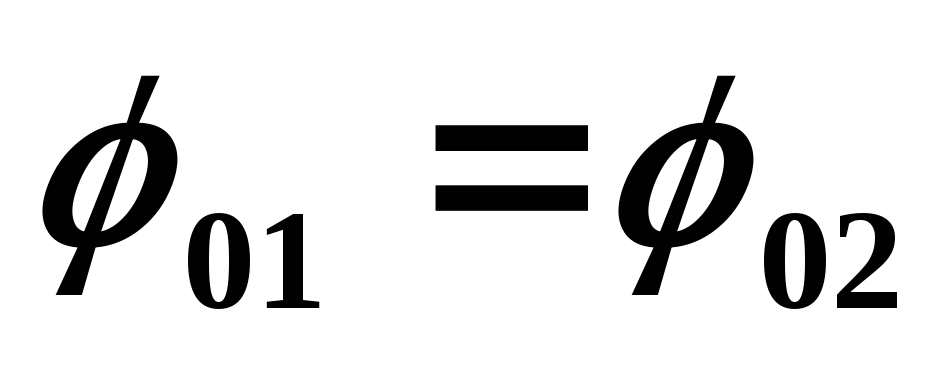1. Пусть , тогда уравнение (16.12) примет вид , откуда 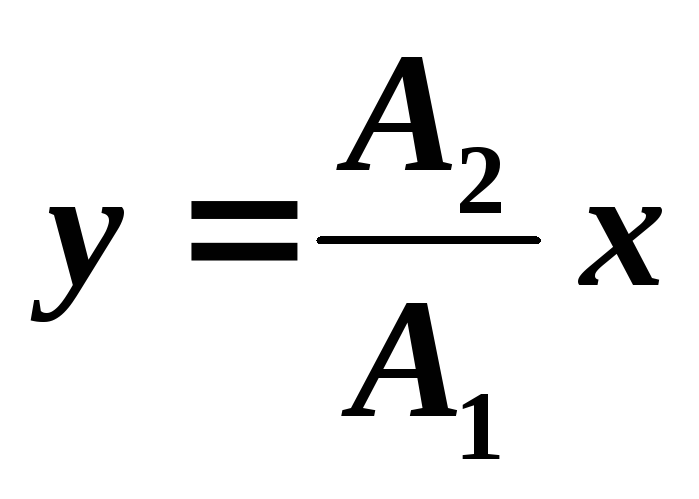- уравнение прямой (рис. 16.8, а).

2. Пусть , тогда уравнение (16.12) после несложных преобразований примет вид 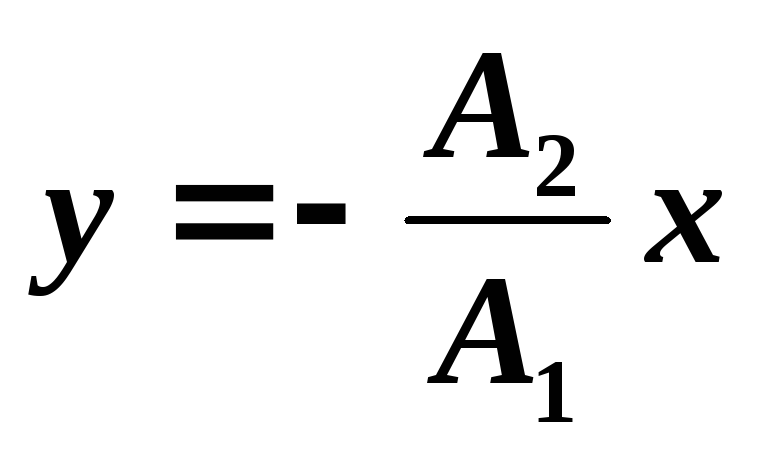-уравнение

прямой (рис.16.8 б).

3. Пусть , тогда уравнение траектории: 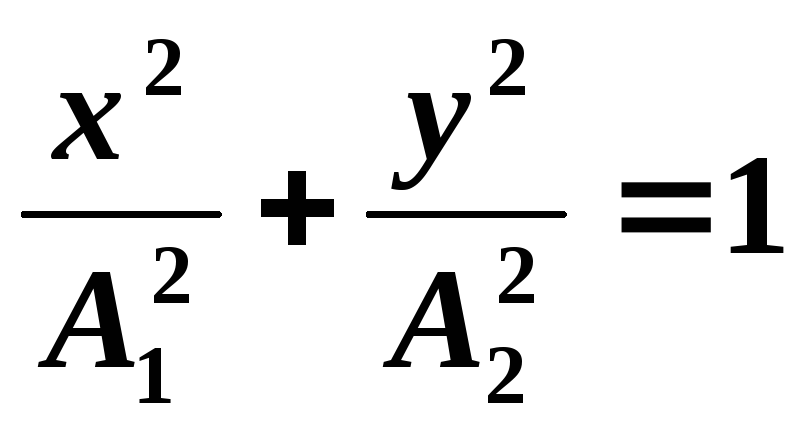- уравнение эллипса. Точка движется по эллипсу, оси которого совпадают с осями координат.

4. При сложении взаимно - перпендикулярных колебаний с различными частотами получаются разнообразные кривые, которые называются фигурами Лиссажу. Форма фигур Лиссажу зависит от соотношения частот, амплитуд и начальных фаз колебаний.