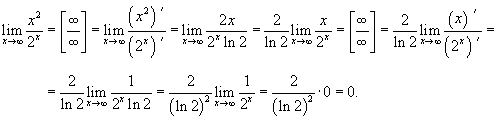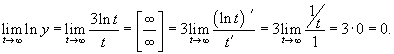МАТАН ЭКЗАМЕН / 36 / правило лопиталя

Правило Лопиталя

Правило Лопиталя представляет собой метод вычисления пределов, имеющих неопределенность  типа  или .  Пусть a является некоторым конечным действительным числом или равно бесконечности. Если  и , то ; Если  и , то аналогично . Это правило впервые упоминалось в книге по дифференциальному исчислению, опубликованной в 1696 (!) году французским математиком Гийомом Лопиталем(1661- 1704). Правило Лопиталя можно также применять к неопределенностям типа . Первые две неопределенности  можно свести к типу  или  с помощью алгебраических преобразований. А неопределенности  сводятся к типу  с помощью соотношения Правило Лопиталя справедливо также и для односторонних пределов.

Пример 1

Вычислить предел . Решение. Дифференцируя числитель и знаменатель, находим значение предела:

Пример 2

Вычислить предел . Решение. Поскольку прямая подстановка приводит к неопределенности типа , применяем правило Лопиталя.

Пример 3

Вычислить предел . Решение. Здесь мы имеем дело с неопределенностью типа . После простых преобразований, получаем

Пример 4

Найти предел . Решение. Используя правило Лопиталя, можно записать

Пример 5

Найти предел . Решение. Здесь мы встречаемся с неопределенностью типа . Обозначим . После логарифмирования получаем        Далее, по правилу Лопиталя, находим        Соответственно,

Пример 6

15. Правила Лопиталя*

Швейцарский математик Иоганн I Бернулли (1667-1748) после успешного окончания Базельского университета, путешествуя по Европе, в 1690 году приезжает в Париж. В литературном салоне философа Никола Мальбранша (1638-1715) Иоганн знакомится с французским математиком маркизом Гийомом Франсуа Антуаном де Лопиталем (1661-1704). В ходе оживленной беседы Лопиталь удивился, как легко, “как бы играя”, юнец Бернулли решал трудные задачи по новому исчислению. Поэтому Лопиталь попросил прочитать ему несколько лекций. Устные беседы понравились Лопиталю, и он за приличный гонорар стал получать материалы в письменном виде. Заметим, что общеизвестное теперь “правило Лопиталя” для раскрытия неопределенностей также было передано ему Иоганном. Уже в 1696 году появился знаменитый трактат Лопиталя “Введение в анализ бесконечно малых для понимания кривых линий”. Вторая часть курса, изложенного Иоганном I Бернулли, была опубликована лишь в 1742 году и называлась “Математические лекции о методе интегралов и другие; написаны для знаменитого маркиза Госпиталия; годы 1691-1692”. В 1921 году были обнаружены рукописные копии лекций, написанные рукой Иоганна I Бернулли, оригиналы которых были переданы Лопиталю в 1691-1692 гг. Из них ученые неожиданно обнаружили, что Лопталь в своем “Анализе” почти не отступал от лекций своего молодого учителя.

Теорема (Коши). Пусть функции  и  непрерывны на , дифференцируемы на  и . Тогда :

Доказательство. Рассмотрим функцию

 выберем так, чтобы выполнялись все условия теоремы Ролля, т.е. .

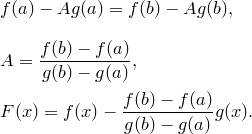
По теореме Ролля существует :

Первое правило Лопиталя

Определение. Пусть функции , непрерывны на , дифференцируемы в , причем . Пусть . Тогда говорят, что отношение  при  представляет собой неопределенность вида .

Теорема. Если при указанных условиях существует

то и

Пусть  конечно. По  выберем : в интервале  выполняется неравенство

Применим теорему Коши к отрезку , где . Существует :

и, значит, 

Это и означает, что .

В случае, когда  бесконечно, неравенство (1) заменяется на

 или 

в зависимости от знака . В остальном доказательство не меняется.

Второе правило Лопиталя

Определение. Пусть функции , непрерывны и дифференцируемы в , причем . Пусть . Тогда говорят, что отношение  при  представляет собой неопределенность вида .

Теорема. Если при указанных условиях существует

то и

Доказательство. Пусть  конечно. По  выберем : в интервале  выполняется неравенство

Определим функцию  из условия

Имеем

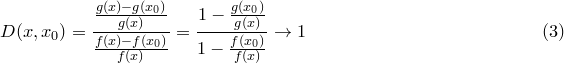
при . Применим к отрезку  теорему Коши. Получим, что существует :

Для тех , для которых 

Так как  произвольно мало, то

В случае, когда , неравенство (2) заменяется на

а неравенство (4) – на неравенство

имеющим место при , достаточно близких к a в силу (3).

Аналогично рассматривается случай .
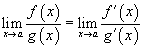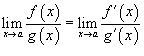
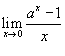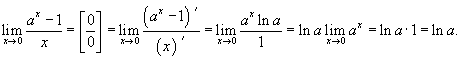
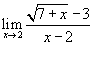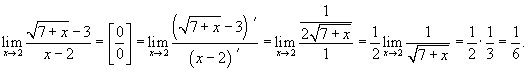
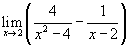