
mechanica-metod / Lab16
.pdfФедеральное агентство по образованию Сибирский государственный аэрокосмический университет
имени академика М. Ф. Решетнева
ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ МАЯТНИКА ОБЕРБЕКА
Методические указания к выполнению лабораторной работы 16
Красноярск 2005
УДК 538.3 (075.5)
Рецензент доктор физико-математических наук,
профессор Ю. Д. ТРОПИН
Определение момента инерции маятника Обербека: Ме-
тодические указания к выполнению лабораторной работы 16 / Сост.: Н. А. Шепета, Т. А. Слинкина, Л. И. Чернышова; СибГАУ. Красно-
ярск, 2005. 18 с.
В методических указаниях дано описание работы по разделу физики «Ме- ханика, молекулярная физика и термодинамика». По содержанию и объему работа соответствует программе курса общей физики для высших технических учебных заведений.
© Сибирский государственный аэрокосмический университет имени академика М. Ф. Решетнева, 2005.
2

Лабораторная работа 16
ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ МАЯТНИКА ОБЕРБЕКА
Цель работы: Изучение законов динамики вращательного движения твердого тела и определение момента инерции маятника Обербека.
1. Кинематика вращательного движения твердого тела
Твердое тело можно рассматривать как систему частиц (атомов или молекул), расположенных в узлах кристаллической решетки. Ес- ли взаимное расположение этих частиц при механическом движении тела изменяется незначительно, то им можно пренебречь и использо- вать модель абсолютно твердого тела.
Абсолютно твердым телом в физике называют тело, размеры, форма и внутренняя структура которого не меняются в процессе его механического движения.
Вращательным называется такое движение твердого тела, при котором все точки его движутся по окружностям, и центры этих ок- ружностей расположены на одной прямой. Эта прямая называется
осью вращения.
Пусть твердое тело произвольной формы вращается вокруг не- подвижной оси ОО′, совпадающей с осью Z, точка О ― начало коор- динат (рис. 1).
Положение произвольной точки М тела будем задавать с по-
мощью радиуса-вектора R . Радиус-вектор любой точки твердого те-
ла R представим суммой
= r + r
R r a,
где a ― радиус-вектор центра инерции (ЦИ) тела, а вектор r опре- деляет расположение точки относительно ЦИ. За малое время dt век- тор r поворачивается в плоскости, перпендикулярной оси ОО′, на малый угол dϕ. На такой же угол поворачивается за время радиус- вектор любой другой точки тела, так как в противном случае рас- стояния между этими точками должны были бы изменяться.
Таким образом, угол поворота dϕ характеризует угловое пере- мещение всего вращающегося тела, за малый промежуток времени.
Удобно ввести вектор dϕ элементарного (малого) поворота
тела, численно равный dϕ и направленный вдоль оси вращения ОО′ так, чтобы из его конца поворот тела был виден происходящим про- тив часовой стрелки (рис. 1). Направление этого вектора совпадает с направлением поступательного движения буравчика, рукоятка кото- рого вращается вместе с телом, т. е. подчиняется правилу буравчика.
Z
О′
ωr
|
dϕ |
ЦИ |
v |
a r
r
M aτ
R
dϕ
x
O
y
Рис. 1
Угловой скоростью тела называют вектор ω, численно равный первой производной от угла поворота ϕ по времени и направленный вдоль оси вращения по правилу буравчика, т. е. так же как вектор элементарного поворота dϕ [3]:
3 |
4 |

|
|
|
r |
|
||
|
r |
|
||||
|
ω = |
dϕ |
, |
(1.1) |
||
|
|
|
||||
|
|
dt |
|
|||
где модуль угловой скорости ω = |
dϕ |
. |
|
|||
|
|
|||||
r |
|
|
dt |
быстроту |
||
Угловая скорость ω характеризует направление и |
||||||
r
вращения тела вокруг оси. Если ω = const, то движение тела называ- ют равномерным вращением вокруг оси.
Скорость v произвольной точки M тела, вращающегося с уг-
r |
|
|
|
|
|
|
|
|
|
ловой скоростью ω, называют линейной скоростью этой точки. За |
|||||||||
время dt точка М проходит по дуге окружности радиуса r путь |
|
|
|||||||
|
dS = vdt = rdϕ, |
|
|
|
|||||
так что |
|
|
|
dϕ |
|
|
|
|
|
|
v = r |
= ωr. |
|
|
(1.2) |
||||
|
|
|
|||||||
|
|
|
|
|
dt |
|
|
|
|
По рис. 1 видно, что вектор v направлен перпендикулярно и к |
|||||||||
r |
|
|
|
|
|
r r |
]. |
Так |
|
ω и к r в ту же сторону, что и векторное произведение |
[ω, r |
||||||||
r |
|
взаимно перпендикулярны, то |
|
|
|||||
как, кроме того, векторы ω и r |
|
|
|
||||||
|
r |
r |
|
= ωr = v. |
|
|
|
||
|
[ω, r ] |
|
|
|
|||||
Следовательно, |
r |
|
|
r r |
|
|
|
||
|
|
v = [ω, r ]. |
|
|
(1.3) |
||||
Для характеристики неравномерного вращения тела вводится
r
понятие углового ускорения. Угловым ускорением называют вектор ε, равный первой производной по времени от угловой скорости:
v |
|
r |
(1.4) |
ε = dω . |
dt
В случае вращения тела вокруг неподвижной оси изменение
r |
|
|
|
|
|
|
|
|
вектора ω обусловлено изменением только его численного значения. |
||||||||
r |
направлен вдоль оси вращения (рис. |
2) в ту же |
||||||
При этом вектор ε |
||||||||
r |
dω |
|
|
|
|
|||
сторону, что и ω при ускоренном вращении |
|
> 0 |
, и в противо- |
|||||
dt |
||||||||
|
|
|
|
|
|
|||
|
|
dω |
< 0 |
|
||||
положную сторону — |
при замедленном вращении |
|
|
[2]. |
||||
|
|
|||||||
|
|
dt |
|
|
|
|||
Тангенциальное ускорение aτ (рис. 1) произвольной точки М
тела, вращающегося вокруг неподвижной оси, связано с угловым ускорением тела:
|
|
a |
= |
dv |
= |
d (ωr) |
= r |
dω |
= εr |
(1.5) |
|||||||||
|
|
|
|
|
|
|
|||||||||||||
|
|
τ |
|
dt |
dt |
|
dt |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
или |
|
|
|
r |
|
r |
r |
|
|
|
|
|
|||||||
|
|
|
|
|
a |
τ = [ε, r ]. |
(1.6) |
||||||||||||
|
dω |
r |
|
|
|
|
|
|
|
|
|
|
dω |
|
|
r |
|
||
|
ω2 |
|
|
|
|
|
|
|
|
|
|
|
|
ω1 |
|
||||
|
|
> 0 |
|
|
|
|
|
|
|
|
|
|
|
|
< 0 |
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
||||
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
ω1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
||
|
|
ε |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω2 |
|
|
|
|
r |
|
|
|
|
v |
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
М |
|
|
|
|
|
|
|
|
|
|
|
М v |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ε |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2
2. Динамка твердого тела, вращающегося вокруг неподвижной оси
Чтобы твердое тело с. неподвижной осью привести во враща-
тельное движение, необходимо хотя бы в одной из его точек приложить r
внешнюю силу F , не проходящую через ось вращения и не параллель-
r
ную ей. Рассмотрим простейший случай, когда сила F лежит в плоско- r
сти, перпендикулярной к оси вращения. При этом действие силы F зависит не только от ее величины, но и от кратчайшего рас- стояния от оси вращения до линии действия силы, называемом плечом l.
Произведение силы на плечо носит название вращательного момента М или момента силы относительно оси вращения (рис. 3):
M = F ×l = Fr sin a |
(2.1) |
5 |
6 |
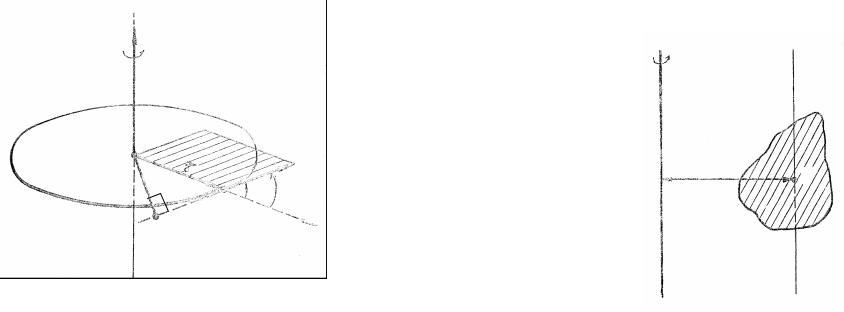
или в векторной форме
r |
(2.2) |
M = [r , F ], |
где r ― радиус-вектор, соединяющий в плоскости действия силы ось с точкой приложения силы F; α ― угол между векторами r и F.
Вектор M считается направленным по оси вращения в сторо- ну, определяемую правилом векторного произведения или правилом правого винта: если вращать головку винта, ориентированного вдоль оси вращения, в направлении действия силы, то поступательное дви-
жение его укажет направление момента M .
В случае, когда на тело действуют несколько сил, результи- рующий момент сил равен векторной сумме моментов отдельных сил. Так как все моменты сил направлены по одной оси, то векторная сумма может быть заменена алгебраической.
M
|
|
|
F |
|
r |
||
|
|
||
|
|
|
|
l |
|
|
α |
|
|
|
|
|
|
|
r |
Рис. 3
Произведение массы материальной точки (частицы) на квад-
рат ее расстояния от оси вращения называется моментом инерции материальной точки относительно этой оси. Сумму моментов инер- ций материальных точек называют моментом инерции тела J отно- сительно заданной оси:
n |
2 . |
|
J = ∑m r |
(2.3) |
|
i i |
|
|
i=1
Всистеме СИ единицей измерения момента инерции является
кг ·м2.
Величина момента инерции зависит не только от массы всего тела и ее распределения в теле, но также от положения тела относи- тельно оси вращения.
Если ось вращения произвольна (рис. 4), то по теореме Штей-
нера момент инерции J тела относительно оси O O′ |
равен сумме мо- |
||||
|
|
1 |
1 |
|
|
|
|
|
′ |
проходящей па- |
|
мента инерции этого тела J0 относительно оси OO , |
|||||
раллельно оси O O′ |
через центр инерции тела, |
и произведению |
|||
1 |
1 |
|
|
|
|
массы этого тела на квадрат расстояния α между осями O O′ и OO′, |
|||||
|
|
|
|
1 |
1 |
(рис. 4): |
|
|
|
|
|
|
|
J = J O + mα 2 . |
|
|
(2.4) |
O′ |
|
O′ |
|
|
|
1 |
|
|
|
|
|
α
C
O1 |
r |
||
O |
|||
Рис. 4 |
|
||
Соотношение |
|
||
|
r |
|
|
r |
|
||
ε = |
M |
(2.5) |
|
J |
|||
|
|
||
7 |
8 |

называют основным законом динамики вращения (или вторым зако- ном Ньютона для вращательного движения). Этот закон формулиру- ется так:
Угловое ускорение, которое тело приобретает под действи- ем момента сил, прямо пропорционально результирующему мо- менту всех внешних сил, приложенных к телу, и обратно пропор- ционально моменту инерции тела относительно некоторой оси.
По формуле (2.5) видно, что угловое ускорение, приобретаемое телом под действием момента силы, зависит от момента инерции те- ла. Чем больше момент инерции, тем меньше угловое ускорение.
Следовательно, момент инерции характеризует инерционные свой- ства тела при вращательном движении подобно тому, как масса
характеризует инерционные свойства тела при поступательном движении. Однако в отличие от массы момент инерции твердого тела может иметь множество значений в соответствии с множеством воз- можных осей вращения. Поэтому, говоря о моменте инерции твердо- го тела, необходимо указать относительно какой оси он рассматрива- ется.
Уравнение (2.5) можно записать так:
r |
r |
|
|
|
|
|
dω |
|
d |
r |
|
||
|
|
|
||||
M = J |
= |
(Jω), |
(2.6) |
|||
dt |
dt |
|||||
|
|
|
|
где J = const.
Произведение момента инерции на угловую скорость вращения называется моментом импульса тела L относительно оси
r |
r |
(2.7) |
Jω = L. |
||
Учитывая (2.7), можно основное уравнение динамики враща- тельного движения (2.5) переписать так:
r |
r |
|
|
dL |
(2.8) |
||
= M , |
dt
т. е. скорость изменения момента импульса тела относительно не-
которой оси равна результирующему моменту относительно той же оси всех внешних сил, приложенных к телу.
Для выяснения физического смысла величины Jω вернемся к рассмотрению движения отдельных точек вращающегося тела [1].
Каждая из этих точек с массой mi движется по окружности радиусом r1.
r
Ее скорость в данный момент времени vi и вектор импульса
r
точки mi vi перпендикулярны к этому радиусу. Таким образом, ради-
r
ус ri является плечом по отношению к mi vi и мы можем (аналогично
моменту силы) ввести понятие момента импульса материальной точки (момента количества движения)
Li = mi viri |
(2.9) |
как произведение величины вектора количества движения на его пле- чо относительно оси вращения.
r
Li
r |
|
r |
mi vi |
|
mi vi |
|
r |
|
|
mi |
|
|
ri |
|
|
|
|
|
Рис. 5 |
|
|
|
|
В векторной форме |
|
|
|
|
|
r |
r |
r |
|
|
|
Li |
= [ri |
, mi vi |
], |
|
(2.10) |
|
|
|
|
r |
|
т. е. векторное произведение радиуса-вектора ri |
материальной точ- |
||||
r |
|
|
|
|
r |
ки на вектор импульса mi vi |
называют моментом импульса L i этой |
||||
|
r |
направлен перпендикулярно к плос- |
|||
материальной точки. Вектор Li |
|||||
|
|
r |
|
r |
|
кости, проведенной через векторы ri |
и |
mi vi и образуют с ними пра- |
|||
r
вую тройку векторов (при наблюдении из конца Li видно, что вра-
r r
щение по кратчайшему расстоянию оси ri к mi vi происходит против часовой стрелки (рис. 5)).
9 |
10 |

Алгебраическая сумма моментов количества движения всех то- чек вращающегося твердого тела носит название момента количест-
ва движения тела L относительно оси (момента импульса тела):
|
n |
|
|
|
|
L = ∑ Li . |
|
(2.11) |
|
|
i=1 |
|
|
|
Подставляя в (2.11) |
выражение для Li |
из (2.9) и, используя |
||
v = ωr, получаем, что |
|
|
|
|
n |
n |
|
n |
= Jw, |
L = ∑m v r |
=∑m wr2 |
= w∑m r2 |
||
i i i |
i i |
|
i i |
|
i =1 |
i =1 |
|
i =1 |
|
т. е. величина Jw есть момент импульса вращающегося тела. Направ- ление Jw совпадает с направлением угловой скорости.
Если внешние силы отсутствуют (замкнутая система) или тако-
вы, что их суммарный момент равен нулю (M внеш = 0), то (2.8) при- нимает вид так называемого закона сохранения момента импульса тела:
J × w = const.
Уравнение (2.5) по формуле сходно с уравнением второго зако-
|
|
|
r |
|
на Ньютона для поступательного движения |
r |
= |
F |
|
|
||||
|
|
|
|
|
|
|
|
m |
|
ления вытекает, что при вращательном движении роль силы играет момент силы, роль массы ― момент инерции и роль линейного уско- рения ― угловое ускорение. Для наглядности дадим это сопоставле- ние в виде таблицы.
|
|
|
Поступательное движение |
|
Вращательное движение около |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
неподвижной оси |
|||
1. |
Линейная скорость v |
1. |
|
|
|
r |
|
|
||||||
Угловая скорость w |
|
|
||||||||||||
2. |
Линейное ускорение a |
2. |
|
|
|
r |
|
|||||||
Угловое ускорение e |
|
|||||||||||||
3. |
Масса m |
|
|
|
3. |
Момент инерции J |
|
|
||||||
|
|
|
r |
|
|
|
4. |
Момент силы M |
|
|
||||
4. |
Сила F |
|
|
|
|
|
||||||||
|
r |
r |
|
|
|
|
|
r |
|
r |
||||
|
|
|
|
|
|
|
|
|
|
= |
||||
5. Импульс тела р = mv |
5. |
Момент импульса L |
J × w |
|||||||||||
6. |
Второй закон Ньютона |
6. |
Второй закон Ньютона |
|
||||||||||
|
d |
|
r |
r |
r |
r |
|
d |
|
r |
r |
r |
r |
|
|
|
|
(mv) = F , ma |
= F |
|
|
|
(Jw) = M , J × e = M |
|
|||||
|
|
|
|
|
|
|
||||||||
|
dt |
|
|
|
|
dt |
|
|
|
|
||||
|
|
|
|
|
|
|
|
Окончание таблицы |
|||||
|
|
|
|
|
|
|
|
|
|
|
|||
Поступательное движение |
Вращательное движение около |
|
|||||||||||
|
|
|
|
|
|
|
неподвижной оси |
|
|
|
|||
7. Кинетическая энергия T = |
mv2 |
7. Кинетическая энергия T = |
|
Jw2 |
|
||||||||
2 |
|
|
2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
l |
|
|
8. Работа момента силы |
|
|
|
||||
8. Работа силы A = ∫ Fdl |
|
|
ϕ |
|
|
|
|||||||
|
|
0 |
|
|
|
A = ∫ Mdj |
|
|
|
||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
9. Связь работы с изменением |
9. Связь работы с изменением |
|
|
|
|||||||||
кинетической энергии |
|
|
кинетической энергии |
|
|
|
|||||||
A = DT = |
mv22 |
- |
mv12 |
|
|
|
A = DT = |
Jw22 - Jw12 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||||
2 |
2 |
|
|
|
2 |
|
|
|
|
|
|||
3. Описание установки и метода измерения
Законы вращательного движения можно изучать при помощи маятника Обербека. Маятник Обербека представляет собой кресто- вину из четырех стержней, расположенных под углом 90º друг к дру- гу, четырех одинаковых цилиндрических грузов, которые можно пе- ремещать по стержням и закреплять на определенном расстоянии от оси вращения и двухступенчатого шкива, установленного на гори- зонтальной оси. Грузы на стержнях устанавливаются симметрично, т. е. так, чтобы центр тяжести маятника лежал на оси вращения. На шкив наматывается нить, к другому концу которой подвешиваются грузы. Грузы вместе с крестовиной удерживаются в покое электро- магнитом.
Кронштейн, к которому прикреплена ось крестовины, можно перемещать вдоль колонки, изменяя таким образом высоту падения груза.
Высоту падения можно измерить по вертикальной шкале. На- чало и окончание движения регистрируются фотоэлектрическими датчиками. Сигналы с датчиков поступают на миллисекундомер, т. е. время падения груза отмечается миллисекундомером.
Момент сил, действующих на шкив можно найти по формуле:
M = F × r, |
(3.1) |
где r – радиус шкива; F – сила натяжения нити, создающая момент.
11 |
12 |
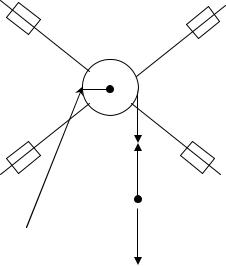
Запишем уравнение движения груза m (рис. 6): |
|
ma = P - F , |
(3.2) |
где a – ускорение груза m.
m1
|
|
|
r |
|
|
|
|
|
|
F |
|
|
|
||
|
|
|
r |
|
|
|
|
|
|
F |
|
|
|
||
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
r |
r |
|
||||
|
|
|
|
|
|||
|
|
|
|
|
|||
|
|
|
|
P = mg |
|
||
|
|
Рис. 6 |
|
|
|||
Выразим из этого уравнения силу натяжения нити F: |
|
||||||
|
|
F = P - ma = m(g - a). |
(3.3) |
||||
Подставив это выражение для силы натяжения F в уравнение |
|||||||
(3.1), получим |
|
|
|||||
|
|
M = m(g − a)r. |
(3.4) |
||||
Используя II закон динамики вращательного движения (2.5), |
|||||||
можно выразить момент сил через угловое ускорение ε |
и момент |
||||||
инерции маятника. Тогда выражение (3.4) можно переписать сле- дующим образом:
J × e = m(g - a)r, |
(3.5) |
||
откуда |
|
||
J = |
m(g - a)r |
. |
(3.6) |
|
|||
|
e |
|
|
Угловое ускорение выражается через линейное следующим об-
разом: |
|
|
|
|
|
|
|
|
|
|
|
|
e = |
a |
. |
|
|
|
|
(3.7) |
|
|
|
|
|
|
|
|
||||
|
|
|
|
r |
|
|
|
|
|
|
Линейное же ускорение можно найти, измеряя путь и время |
||||||||||
при равноускоренном движении груза m: |
|
|
|
|||||||
|
|
a = |
2h |
, |
|
|
(3.8) |
|||
|
|
|
t 2 |
|
|
|||||
|
|
|
|
|
|
|
|
|
||
где h – путь груза; t – время его движения. |
|
|||||||||
Подставив (3.7) и (3.8) в уравнение (3.6), получим формулу |
|
|||||||||
|
|
|
|
2h |
2t 2 |
|
||||
m g - |
|
|
|
r |
|
|||||
t 2 |
|
|
||||||||
J = |
|
|
|
|
|
|
. |
(3.9) |
||
|
2h |
|
|
|
||||||
|
|
|
|
|
|
|
||||
Используя формулу (3.9), можно найти момент инерции маят- ника Обербека на основе определенных опытным путем величин m, h, r, t. Момент инерции маятника можно рассчитать (теоретически) по формуле
J |
|
= J |
0 |
+ 4m R2 |
+ 4 |
M × L2 |
, |
(3.10) |
T |
|
|||||||
|
|
1 1 |
3 |
|
|
|||
|
|
|
|
|
|
|
||
где J 0 – суммарный момент инерции двухступенчатого шкива, оси и втулки крестовины (его можно рассчитать как сумму моментов инер- ции двух дисков); 4m1R12 – момент инерции четырех подвижных гру- зов крестовины; R1 – расстояние от оси вращения до центра тяжести подвижного груза m1 (на крестовине); m1 – масса подвижного груза
(на крестовине); |
4 |
M × L2 |
– момент инерции 4-х стержней крестови- |
|
|||
|
3 |
|
|
ны (без грузов); |
L – длина стержня; M – масса стержня без груза. |
||
Подготовка прибора к измерениям |
|||
1. Нажать клавишу «СЕТЬ» и проверить горят ли индикаторы обоих фотоэлектрических датчиков и все ли индикаторы миллисе- кундомера высвечивают цифру ноль.
13 |
14 |
2.Переместить груз m в верхнее положение, наматывая нить на один из шкивов. Проверить, находится ли система в состоянии покоя, т. е. действует ли верхний электромагнит.
3.Нажать клавишу «ПУСК» и проверить движется ли система
иизмеряет ли секундомер время падения груза.
4.Нажать клавишу «СБРОС» и проверить произошло ли обну- ление секундомера, и выключился ли тормозной (нижний) электро- магнит.
5.Переместить груз m снова в верхнее положение, отжать кла- вишу «ПУСК» и проверить произошла ли повторная блокировка сис- темы.
Измерения
1.Установить выбранный груз m и расположить его так, что- бы нижний край груза совпал с чертой на корпусе верхнего фото- электрического датчика. Записать величину массы груза m в табли- цу.
2.Измерить по шкале и записать в таблицу высоту падения h.
3.Нажать клавишу «ПУСК» и записать время падения груза m.
4.Нажать клавишу «СБРОС», вызывающую обнуление милли- секундомера.
5.Повторить измерение времени падения груза не менее пяти раз (пункты 1, 3 и 4), каждый раз записывая результат в таблицу.
Найти значение времени tср по формуле
|
|
1 |
n |
tср |
= |
|
∑ti , |
|
|||
|
|
n i =1 |
|
где ti – значение времени падения груза m при i-том измерении, n – число измерений.
6.Повторить измерения по пунктам 1–5 для различных масс падающих грузов (до 3-х разных масс).
7.Рассчитать по формуле (3.9) момент инерции маятника Обербека (по средним значениям времени падения груза), определяя момент инерции три раза (для различных m). Занести результаты в таблицу.
8.Найти среднее значение момента инерции
|
|
1 |
k |
Jср |
= |
|
∑Ji , |
|
|||
|
|
k i =1 |
|
где k – число измерений. Записать Jср в таблицу.
9. Вычислить теоретическое значение момента инерции маят- ника Обербека JT по формуле (3.10).
Расчет погрешности измерения момента инерции
Относительная погрешность измерения момента инерции опре- деляется по формуле
d = JT - J ср ×100 %,
JT
где JT – теоретический момент инерции маятника, определяемый по формуле (3.10); Jср – среднее значение найденного эксперименталь- ного момента инерции.
k № |
m (кг) |
t |
tср |
h |
Ji |
Jср |
JT |
δ |
|
(c) |
(с) |
(м) |
(кг·м2) |
(кг·м2) |
(кг·м2) |
11
2
3 (53,9 + 39,6) ·10–3
4
5
21
2
(53,9 + 39,6 +
3 + 42,2) · 10–3
4
5
31
2 (53,9 + 39,6 +
3 + 42,2 + 39,9) · 10–3
4
5
Контрольные вопросы
15 |
16 |
1.Какие тела называют абсолютно твердыми?
2.Какое движение называют вращательным?
3.Какие физические характеристики называют моментом инерции материальной точки, твердого тела?
4.Что характеризует момент инерции?
5.Укажите силы, действующие на падающий груз m в этой ра-
боте;
6.Каков характер движения груза m?
7.Какому закону динамики подчиняется его движение?
8.Найдите силу, сообщающую грузу m ускорение?
9.Какая сила создает вращающий момент, действующий на маятник Обербека и как найти ее значение?
10.Изменится ли момент инерции маятника Обербека, если подвесить на нить груз другой массы или намотать нить на диск дру- гого диаметра?
11.Изменится ли вращающий момент, действующий на маят- ник, если подвесить на нить груз другой массы?
12.Изменится ли угловое ускорение маятника, если подвесить на нить груз другой массы?
13.Какие характеристики изменятся, если нить намотать на шкив другого радиуса?
14.Сформулируйте основной закон динамики вращательного движения.
Библиографический список
1.Детлаф, А. А. и др. Курс физики / А. А. Детлаф, Б. М. Явор-
ский. Т. 1. М.: Высш. шк., 1999.
2.Савельев, И. В. Курс общей физики: в 5-ти кн. Кн. 1. Меха- ника / М.: Астрель-АСТ, 2001.
3.Трофимова, Т. И. Курс физики / Т. И. Трофимова. М.: Высш.
шк., 1998.
17
Методическое издание
ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ МАЯТНИКА ОБЕРБЕКА
Методические указания к выполнению лабораторной работы 16
Составители: ШЕПЕТА Н. А., СЛИНКИНА Т. А.,
ЧЕРНЫШОВА Л. И.
Подписано в печать 12.01.2005. Формат 60×84/16. Бумага офисная. Гарнитура «Таймс». Печать плоская. Уч.-изд. л. 2,5. Усл. п. л. 2,09.
Тираж 200 экз. Заказ С
Отпечатано в отделе копировально-множительной техники СибГАУ. 660014, г. Красноярск, просп. им. газ. «Красноярский рабочий», 31.
18
