Собственные (резонансные) частоты стоячих волн.

На практике в случае свободных колебаний некоторых физических систем, например струн, столбов газа и др., устанавливаются стоячие волны, частоты которых удовлетворяют определенным условиям, т. е. могут принимать только определенные дискретные значения, называемые собственными частотами данной колебательной системы.

Рис. 10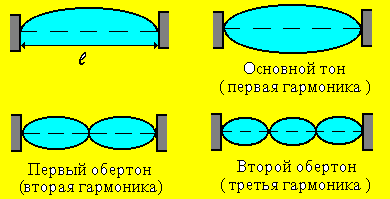

Например, в точках закрепления струн или стержней размещаются узлы смещения (пучности деформаций), а на свободных концах стержней  пучности смещения (узлы деформации). При колебаниях воздушного столба в цилиндрической трубке у закрытого конца трубки размещается пучность давления, а у открытого  узел давления. В качестве примера рассмотрим возникновение стоячих волн при изменении натяжения колеблющейся струны (параметрический резонанс). Частоты стоячих волн называют собственными, или резонансными, т. к. такие колебания сопровождаются резонансными явлениями. В отличие от пружинного, математического или физического маятников, которые при колебаниях имеют одну собственную резонансную частоту (одна степень свободы), натянутая струна имеет много резонансных частот.

Эти частоты в свою очередь кратны низшей частоте.

Более продолжительное время сохраняются те волны, которым соответствуют резонансные частоты. В точках закрепления струны возникают узлы (рис. 10). Для нахождения резонансных частот воспользуемся тем, что длина стоячей волны связана с длиной самой струны: = m , где m = 1, 2, 3, ... , и определяет число гармоник.

Например, основной тон (мода)  первая гармоника, соответствует пучности, а длина струны ₁ = , (m = 1; ₁  длина волны первой гармоники). Для второй гармоники  ₂ = ₂ (m = 2; ₂  длина волны второй гармоники), для третьей  ₃ = 2 ₃/3 (m = 3; ₃  длина волны третьей гармоники) и т. д. Частоты колебания стоячей волны можно найти по формуле

 = m .

Замечание: Стоячая волна может существовать только при строго определенных частотах колебаний.

Действительно, по условию при отсутствии колебаний на правом конце закрепленной струны, где координата х = , а амплитуда обращается в нуль и разность фаз  = ₀ = , то

А_ст = 2Аcos(kx  )= 2Asinkx.

В точках, где sin(kx) = 0, возникнут узлы и sin(k ) = 0.

Следовательно,

k = m. (53)

Общий вывод: Полученный результат является необычным для классической физики, потому что k и  могут принимать строго определенные значения:

k = m ,

 = m .

Наблюдаемое аномальное явление весьма существенно повлияло на разгадку квантовых явлений.

Согласно выводам квантовой теории следует, что все микрообъекты обладают корпускулярными и волновыми свойствами.