35 Вопрос
ОБЩЕЕ РЕШЕНИЕ ЛИНЕЙНОГО ОДНОРОДНОГО ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ВТОРОГО ПОРЯДКА С ПОСТОЯННЫМ КОЭФФИЦИЕНТОМ
Способ
построения фундаментальной системы
решений принадлежит Эйлеру, который
предложил искать решения в виде
где k = const.
Тогда, принимая во внимание, что
исходное линейное однородное
дифференциальное уравнение можно
записать следующим образом:
Откуда,
учитывая отличие от нуля множителя
получим характеристическое уравнение
Из
этого уравнения находим неизвестный
параметр k,
а затем определяем функции
удовлетворяющие однородному
дифференциальному уравнению. Наиболее
просто корни
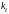характеристического уравнения
определяются для квадратного уравнения
для которого
где
дискриминант
В зависимости от знака и величины D возможны следующие исходы.
1. Если
D > 0,
то корни
характеристического уравнения вещественны
и различны. Для решений линейного
однородного дифференциального уравнения
и
Функции
линейно независимы и образуют
фундаментальную систему решений. В
соответствии с теоремой о структуре
общего решения такого уравнения можем
записать
2.
Если D = 0,
то характеристическое уравнение имеет
один корень кратности два
Следовательно, в этом случае метод Эйлера позволяет определить только одно решение дифференциального уравнения
Второе решение этого уравнения, линейно независимое с первым имеет вид
Поэтому
функции
линейно независимы и образуют
фундаментальную систему решений для
рассматриваемого дифференциального
уравнения. Его общее решение
может быть записано в виде
3. Если
D < 0,
то характеристическое уравнение имеет
два комплексно-сопряженных корня
k1,2 = i,
где = 0,5а1,
.
Соответственно, ДУ имеет два
комплексно-сопряженных решения, которые
с помощью формулы Эйлера можно представить
в виде
.
Образуя подходящие линейные комбинации
функций
и
находим два вещественных решения
и
,
где
= 0,5а1,
можно убедиться в том, что они являются
его решениями.
Функции
и
линейно независимы и образуют
фундаментальную систему решений
рассматриваемого дифференциального
уравнения. Его общее решение
может быть записано следующим образом:
Пример.
Решить уравнение
Решение.
Это линейное однородное дифференциальное
уравнение второго порядка, коэффициенты
которого а1 = 4
и а2 = 3.
Характеристическое уравнение имеет
дискриминант
Следовательно, корни
характеристического уравнения
и
различны. Фундаментальной системой
решений заданного дифференциального
уравнения являются функции
и
Общее решение уравнения записывается
следующим образом:
Пример.
Решить уравнение
Решение.
В характеристическом уравнении
коэффициенты а1 = -6
и а2 = 9,
поэтому дискриминант D = 0.
Следовательно, характеристическое
уравнение имеет один корень
Фундаментальную систему решений
заданного уравнения образуют функции
и
а общее решение уравнения может быть
записано в виде
Пример..
Решить уравнение
Решение.
В характеристическом уравнении
коэффициенты а1 = 4,
а2 = 5,
поэтому дискриминант D = -1<0.
Следовательно,
и фундаментальную систему решений
заданного уравнения образуют функции
и
Общее решение заданного дифференциального
уравнения записывается в виде
