2. Принцип действия и методические погрешности акселерометров.

Датчиками первичной инерциальной информации являются измерители ускорений - акселерометры, основанные законах классической механики Ньютона.

Простейший осевой акселерометр (рис. 15.5) состоит из инерционной массы m, с помощью пружины прикрепленной к основанию. При движении ос­нования в направлении оси X, называемой осью чувствительности акселерометра, с ускорением а^к к массе m будет приложена сила инерции F = m • а^к, в результате чего масса станет перемещаться относительно шкалы в направлении, противоположном вектору ускорения. Со стороны пружины на массу будет действовать обратная по знаку силе F сила

Fпр = Кпр * ΔX,

Рис.15.5. Принцип работы акселерометра

Рис.15.6. Маятниковый акселеро­метр с электрической пружиной

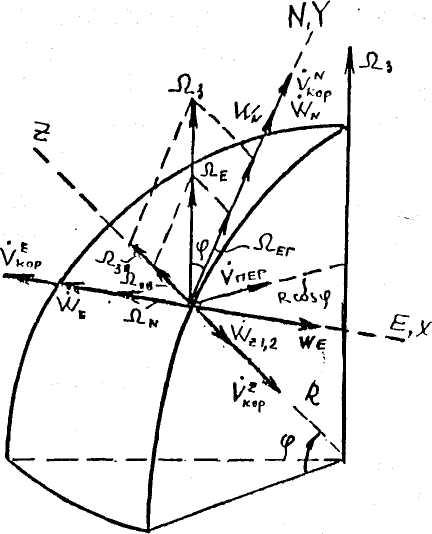
Рис. 15.7.К определению методических погрешностей акселерометра

где К_Пр - коэффициент жесткости пружины;

ΔХ - линейная величина перемещения массы.

По окончании переходного процесса сила F_пр уравновесит силу F, при этом величина ΔХ оказывается пропорциональной измеряемому ускоре­нию:

С помощью потенциометра значение ΔХ может быть преобразовано в электрический сигнал, пропорциональный а^к.

Акселерометры измеряют только ускорения, обусловленные действием негравитационных сил, и не измеряют ускорений, вызванных гравитацией. Действительно, если основание, на котором установлен акселерометр, движется к земле с ускорением силы тяжести g (полагаем, что а^к = 0), то, поскольку сила тяжести одинаково действует и на основание, и на массу m акселерометра, перемещения массы относительно нулевой отметки шкалы не будет.

Если а^к - ускорение, создаваемое разностью сил тяги и лобового сопротивления, то полное абсолютное ускорение основания будет, а = а^к - (-g). Знак " - " перед g учитывает отрицательное направление вектора g по оси X. Акселерометр же измерит только ускорение а^к, то есть будет иметь место методическая погрешность в измерении полного абсолютного ускорения, равная ускорению силы тяжести. Поэтому в общем случае использование инерциальных систем возможно только в известном поле гравитации. Ускорение а^к, измеряемое акселерометром, часто называют "кажущимся", при этом:

а^к = а - g.

В случае горизонтального полета (на постоянной высоте) подъемная сила ЛА уравновешивает силу тяжести. За счет подъемной силы Y в верти­кальном направлении создается ускорение а^к_у. В горизонтальном полете вертикальной составляющей ускорения нет, поэтому, а = а^к_у + g = 0, откуда а^к_у = -g, т.е. в этом случае акселерометр с вертикальной осью чувствительности будет измерять ускорение, создаваемое подъемной силой, численно равное, но противоположное по знаку ускорению силы тяжести. Именно в этом смысле следует понимать встречающееся утверждение, что "акселерометр реагирует на ускорение силы тяжести".

Кроме осевых акселерометров в инерциальных системах применяются маятниковые акселерометры, причем у тех и у других для повышения точ­ности работы и диапазона измерений, ограниченных гистерезисом пружины, вместо механической пружины используется электрическая пружина.

Маятниковый акселерометр с электрической пружиной (рис. 15.6) ра­ботает следующим образом. При движении ЛА в направлении оси X чувстви­тельности прибора с ускорением а^к к массе маятника m, укрепленной на плече 1, будет приложена сила инерции F, создающая относительно оси Z момент силы инерции М = mlа^к, в результате чего маятник станет пово­рачиваться вокруг оси Z. Угол поворота маятника с помощью датчика угла ДУ (потенциометрического, индукционного или другого типа) преоб­разуется в напряжениеU_β = К_ду * β ( К_ду - крутизна характеристики датчика угла), которое после усиления в усилителе до величины U_y = K_y* U_β> (K_y - коэффициент усиления усилителя) подается на датчик момента ДМ. Последний прикладывает к оси Z подвеса маятника момент об­ратной связи

где К_дм - крутизна характеристики датчика момента;

К_эп = К_ду * К_у * К_дм - коэффициент передачи электрической пружины, таким образом, элементами электрической пружины являются датчик угла, усилитель и датчик момента.

В установившемся режиме момент обратной связи уравновесит момент ил инерции, так что угол поворота маятника и напряжение на выходе усилителя оказываются пропорциональны ускорению:

и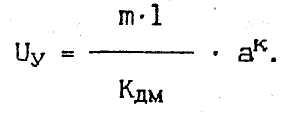

При повороте маятника вместе с ним на угол в повернется и ось чувствительности. При этом акселерометр будет измерять не все ускоре­ние а^к, а его составляющую а^К, = a^K cos β.

Кроме того, акселерометр станет реагировать и на поперечные ускорения, направленные вдоль оси Y. Это обстоятельство приводит к методи­ческой погрешности, уменьшение которой возможно за счет уменьшения угла , что достигается увеличением коэффициента усиления усилителя.

Рассмотренные акселерометры имеют отрицательную обратную связь, обусловленную наличием пружины (механической или электрической). Поэ­тому такие приборы называют компенсационными.

Ввиду того, что опору с меньшим трением легче изготовить в случае вращательного движения массы m, чем в случае ее поступательного движе­ния, то в инерциальных системах навигации наибольшее применение нашли маятниковые акселерометры.

Пороговая чувствительность современных акселерометров с электри­ческой пружиной составляет порядка 10^-4 - 10^-5 g.

Акселерометры имеют также методические погрешности, обусловленные собственным вращением Земли и перемещением ЛА относительно Земли. Эти погрешности удобно анализировать по уравнениям акселерометров в 1-й или 2-й форме.

Первая форма связывает измеряемые ускорения с абсолютными линей­ными скоростями ЛА, абсолютными угловыми скоростями вращения ГСП в инерциальной системе отсчета и составляющими удельной гравитационной

силы

Вторая форма измеряемые ускорения связывает с составляющими путе­вой скорости, относительными угловыми скоростями вращения ГСП и сос­тавляющими удельной силы тяжести g_T.

Более просто выводятся и выглядят уравнения акселерометров в пер­вой форме. Выше было показано, что акселерометр измеряет не абсолют­ное, а кажущееся ускорение:

Приведенные зависимости записаны в общем виде, в инерциальной же системе отсчета

Определим вначале значение абсолютного ускорения. В соответствии с теоремой о производной от вектора во вращающейся системе координат:

где:

- производная абсолютной скорости в инерциальном пространстве;

- производная абсолютной скорости в относительной (связанной с Землей) системе координат;

- абсолютная угловая скорость вращения ГСП;

- векторное произведение скоростей.

Далее разложим по осям с учетом правила для произведения двух векто­ров:

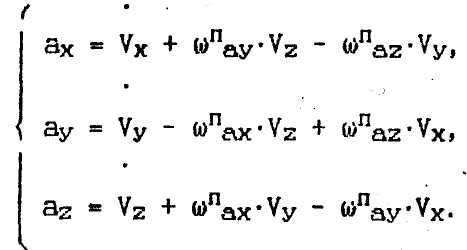
Теперь, помня, что для инерциальной системы координат(- вектор удельной гравитационной силы), определим окончательно составляющие абсолютной скорости, значения которых и есть уравнения аксе­лерометра в 1-й форме:

где V_x(t_o), V_y(t_o), V_z(t_o) - начальные значения абсолютной скорости;

g_ox, g_oy, g_oz - составляющие вектора удельной гравитационной силы;

a^K_X, a^K_y, а^К_z - сигналы акселерометров. Из уравнений видно, что для определения скорости (а в последующем и линейных координат) интегрирования одних только сигналов акселеро­метров недостаточно, необходимо учитывать остальные члены в подынтег­ральном выражении. Эти члены носят название компенсационных, и неучет их приводит к появлению основных методических погрешностей акселеро­метров. Компенсационные члены имеют первый или второй порядок малости и не учитываются только в ИКВ-системах. Такое упрощение объясняется следующими рассуждениями:

1)м/с² - второй порядок малости;

2. среднее значение вертикальной скорости Vz за весь полет близко к нулю и в любой момент времени обычно меньше Vx и Vy, - следовательно, членами о Vz также можно пренебречь;

3. при компенсации кажущегося ухода ГСП в азимуте даже только из-за суточного вращения Земли (по закону),члены с для максимальных значений скоростей не превышают 3,5 • 10^-2 м/с²; если же компенсируется и уход ГСП из-за движения ЛА, то члены с w^п_az имеют еще меньший порядок малости;

4) Vz и в особенности вертикальная координата z в ИКВ-системах не вычисляются вследствие вычислительной неустойчивости вертикального канала; в остальных ИНС также из-за вычислительной неустойчивости канала вычисляется только значение Vz.

Полные уравнения акселерометров во 2-й форме имеют вид:

Таким образом, для ИКВ-систем алгоритм вычисления скоростей выгля­дит так:

где: W - путевые скорости;

- угловые скорости вращения ГСП относительно Земли;

- угловые скорости вращения Земли;

- составляющие удельной силы тяжести.

В ИНС используется как 1-я, так и 2-я Формы уравнений.

Основой любой ИНС является ИКВ. Все ИКВ - это фактически ГСП, удерживаемые в заданном положении специальными гиростабилизаторами.