
дз на зиму КиЦОИ / tspd-06
.pdf
Глава 6 Обнаружение и исправление
ошибок
E-mail: abilov@udm.ru
Web: http://www.istu.ru/unit/prib/net/edu/teach/tspd
Лекция 6. Обнаружение и исправление ошибок |
1 |
 1. Введение
1. Введение
Типыошибок
Причины появления ошибок передачи данных: внешние помехи,
интерференция, неисправности и прочие факторы в сетях
Требование многих приложений: гарантия идентичности передаваемых и принимаемых данных
Некоторые приложения (передача аудио и видео) допускают ошибки
Другие приложения (передача текста, графика и др.) более требовательны к допустимому уровню ошибок
Передаваемые данные могут быть искажены. Для некоторых приложений необходимы функции обнаружения и/или коррекции ошибок
Типы ошибок:
Одиночная ошибка (происходит инверсия одного двоичного символа)
Пакетная ошибка (инвертируется несколько бит в блоке)
Импульсная помеха – 0,01 с, скорость передачи данных – 1200 бит/с:
инвертируется до 12 бит информации
Лекция 6. Обнаружение и исправление ошибок |
2 |
 1. Введение
1. Введение
Типыошибок: одиночнаяошибка
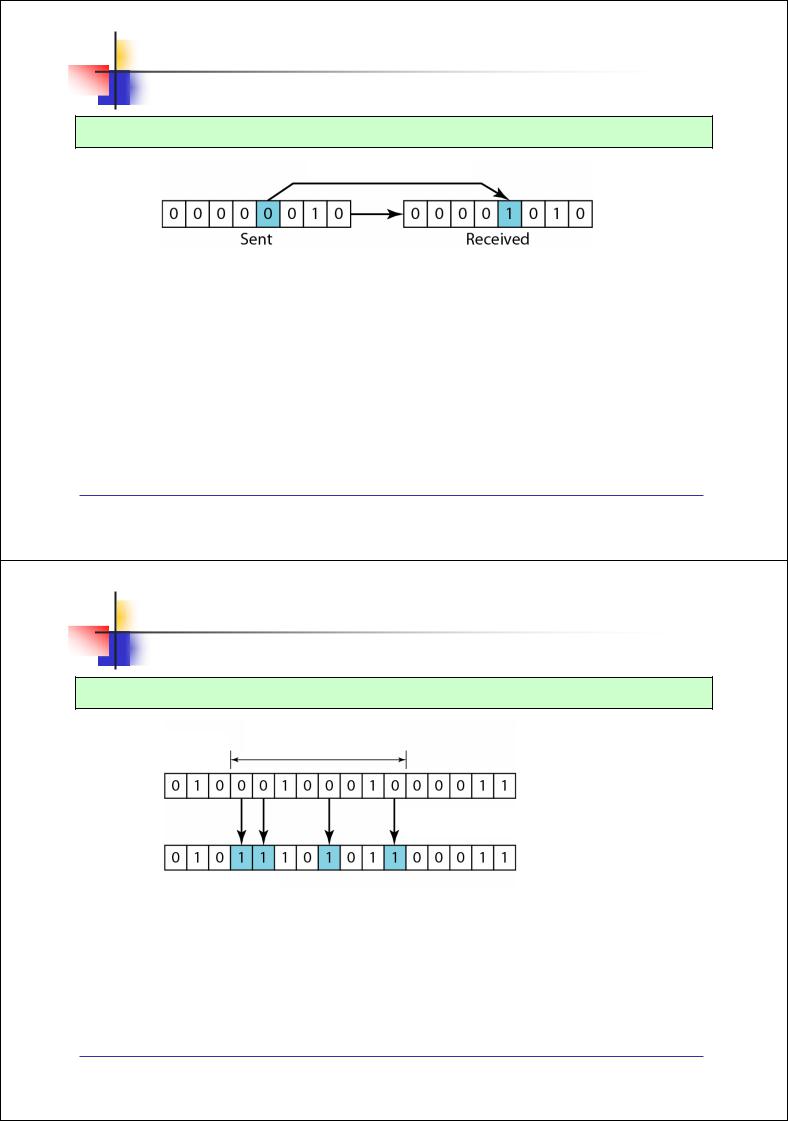
При одиночной ошибке инвертируется лишь один бит в блоке данных
Инверсия бита
Передаваемый блок |
|
Принимаемый блок |
Рис. 3.1. Одиночная ошибка
Посылаемый блок (код): 00000010 (ASCII STX) – Start of text (Начало текста) Принимаемый блок (код): 00001010 (ASCII LF) – Line feed (Перевод строки)
Одиночные ошибки менее вероятны по сравнению с пакетными ошибками
При скорости передачи данных 1 Мбит/с, длительность бита равна лишь 1 мкс
Большинство помех имеет значительно большую длительность
Лекция 6. Обнаружение и исправление ошибок |
3 |
 1. Введение
1. Введение
Типыошибок: пакетнаяошибка
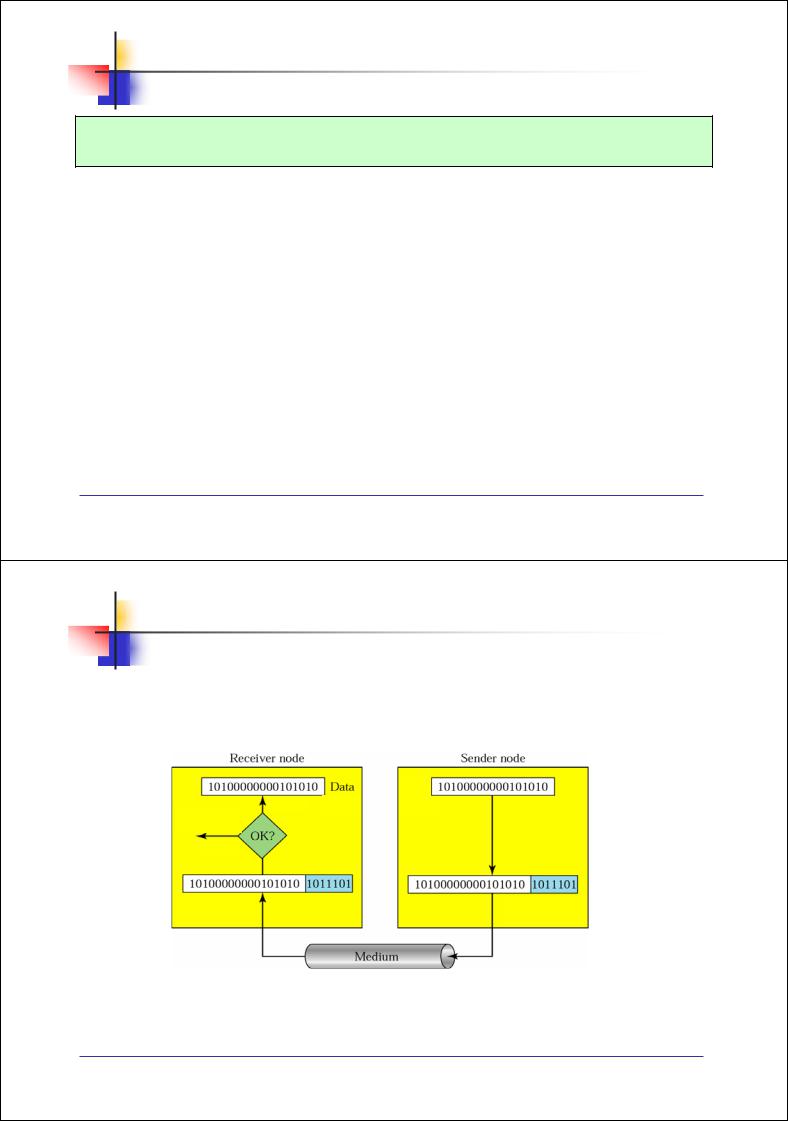
При пакетной ошибке инвертируется два или более бит в блоке данных
Длина пакетной Передаваемый ошибки (8 бит)
блок
Искаженные биты
Принимаемый блок Рис. 3.2. Пакетная ошибка длинной 8 бит
Искаженные биты не обязательно следуют друг за другом
Длина пакетной ошибки: от первого до последнего искаженного бита, определяется скоростью передачи данных и длительностью помехи
Пакетные ошибки более вероятны по сравнению с одиночными ошибками
Скорость передачи 1 кбит/с, длит. помехи 0,01 с – искажаются до 10 бит
Скорость передачи 1 Мбит/с, длит. помехи 0,01 с – искажаются до 10000 бит
Лекция 6. Обнаружение и исправление ошибок |
4 |
 1. Введение
1. Введение
Контрольошибокиизбыточность(Redundancy)
Для обнаружения или исправления ошибок к блоку полезной информации добавляется избыточность (добавочные биты)
По избыточным битам на приемной стороне обнаруживаются или исправляются искаженные биты информации
Обнаружение ошибок (Error Detection): определяется лишь факт наличия ошибок, при этом их тип (одиночная или пакетная ошибка), количество и место положение не имеют значения
Исправление ошибок (Error Correction): определяется точное количество искаженных бит и их местоположение в блоке
Прямое исправление ошибок (Forward error correction – FEC): поврежденный блок восстанавливается с помощью избыточности (исправить можно ограниченное количество ошибок)
Ретрансляция (Retransmission): при обнаружении ошибок в блоке запрашивается его повторная передача
Лекция 6. Обнаружение и исправление ошибок |
5 |
 1. Введение
1. Введение
Кодирование(Coding)
Принцип помехоустойчивого кодирования: на передаче к информационному коду вводится избыточность по определенному правилу; на приеме проверяется соотношение полезной и избыточной комбинации
Приемник |
|
|
|
Передатчик |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Да Данные Данные
Потеря
данных
Нет
Информация и избыточность
Две разновидности схем кодирования:
Блочное кодирование
Сверточное кодирование
Информация и избыточность
Рис. 3.3. Кодирование
Лекция 6. Обнаружение и исправление ошибок |
6 |

 1. Введение
1. Введение
Модульнаяарифметика(Modular Arithmetic)
Одна из функций кодирования и декодирования: операции сложения и умножения в соответствии с правилами для алгебраического поля с ограниченным количеством элементов
Поле Галуа: алгебраическое поле с q элементами – GF(q):
Для двоичной системы счисления q = 2 (элементы 0 и 1)
Простейшее поле – это поле GF(2)
В общем случае если q – простое целое число, ограниченное поле GF(q) состоит из элементов {0, 1, …, q – 1}
Операции сложения и умножения над элементами из GF(q) осуществляется по модулю q
Варифметике по модулю q используются только целые числа
вдиапазоне от 0 до q–1, включительно
Лекция 6. Обнаружение и исправление ошибок |
7 |
 1. Введение
1. Введение
Арифметикапомодулю2 (Modulo-2 Arithmetic)
Арифметика по модулю 2: используется в большинстве случаем при передаче данных
Примеры таблиц сложения и умножения для GF(2) |
+ |
0 |
1 |
• |
0 |
1 |
|
0 |
0 |
1 |
0 |
0 |
0 |
||
|
|||||||
|
1 |
1 |
0 |
1 |
0 |
1 |
Операция сложения (и вычитания) по модулю 2 соответствует операции XOR (исключающее ИЛИ). Примеры операции XOR:
Два одинаковых бита: результат – 0
Два разных бита: результат – 1 |
|
Операция XOR для двух слов |
|
|
|
Рис. 3.4. Операция XOR
Если оба элемента одинаковы – результат 0; если элементы разные – результат 1
Лекция 6. Обнаружение и исправление ошибок |
8 |
 2. Блочноекодирование
2. Блочноекодирование
Информационное слово (Dataword): блоки длиной k бит, на которые делится исходная двоичная информационная последовательность
Избыточные символы (Redundancy): добавляются по определенному правилу (r бит) к информационному слову на передаче
Кодовое слово (Codeword): двоичный вектор (комбинация) фиксированной длины n = k + r бит; формируется при блочном кодировании
Блочное кодирование (Block Coding):
Образуется множество из 2k информационных слов длиной k и множество из 2n кодовых слов длиной n
Так как n > k, то количество комбинаций кодовых слов больше количества комбинаций информационных слов
Блочное кодирование подразумевает взаимно-однозначное соответствие информационных и кодовых слов
При кодировании не используются 2n – 2k кодовых слов
Разрешенные слова (комбинации): комбинации, используемые при кодировании
Лекция 6. Обнаружение и исправление ошибок |
9 |
 2. Блочноекодирование
2. Блочноекодирование
k бит k бит k бит
2k комбинаций информационных слов длиной k бит
n бит |
|
n бит |
|
n бит |
2n комбинаций кодовых слов длиной n бит (из них 2k разрешенных)
Рис. 3.5. Множества информационных и кодовых слов в блочном кодировании
Деление на |
|
|
|
блоки |
k бит |
k бит |
k бит |
|
Блочное кодирование:
Компенсирует недостатки линейного кодирования ненадежного физического уровня
может использоваться как для синхронизации, так и для обнаружения ошибок
|
|
|
|
|
|
Добавление |
|
|
|
|
|
|
избыт. бит |
n бит |
|
n бит |
|
n бит |
||
|
|
|
|
Линейное
кодирование
Рис. 3.6. Блочное кодирование
Лекция 6. Обнаружение и исправление ошибок |
10 |
 2. Блочноекодирование
2. Блочноекодирование
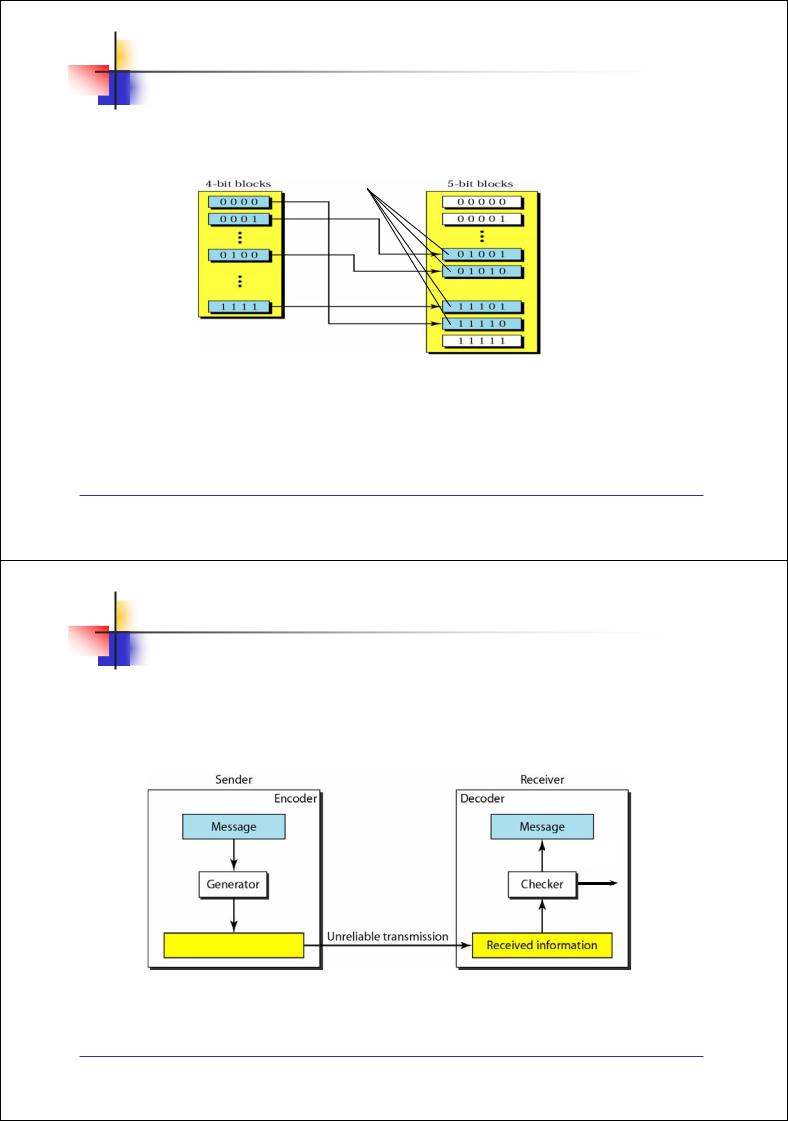
Пример1 Рассмотрим блочный код 4B/5B : исходная информационная последовательность двоичных символов делится на информационные слова длиной k = 4 бит. Кодер заменяет каждое слово на соответствующее кодовое слово длиной n = 5 бит
k = 4 |
|
Разрешенные слова |
|
n = 5 |
Рис. 3.7. Замена комбинаций
вблочном кодировании
Множество из 16 комбинации информационного слова отображается лишь на часть (разрешенных) комбинаций кодового слова; остальные не используются
Каждый код должен содержать не более одного нулевого бита вначале кода (слева) и не более двух нулевых бит в конце (справа)
кодовые слова не могут содержать более чем три последовательных нулевых бита, что облегчает тактовую синхронизацию
Лекция 6. Обнаружение и исправление ошибок |
11 |
 2. Блочноекодирование
2. Блочноекодирование
Обнаружениеошибок
Два условия возможности обнаружения искажений в кодовом слове:
Приемник обладает списком разрешенных комбинаций кодового слова
Передаваемое кодовое слово в результате искажений преобразуется в одну из
разрешенных комбинаций
|
|
Передатчик |
|
|
|
|
|
|
|
|
|
Приемник |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Кодер |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
Декодер |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
Информация |
|||||||||||||
Информация |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Извлечение |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Потеря |
|
||||||
|
|
Генератор |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
Детектор |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Информационная и |
|
|
Ненадежная передача |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
Принятый код |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
избыточность |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
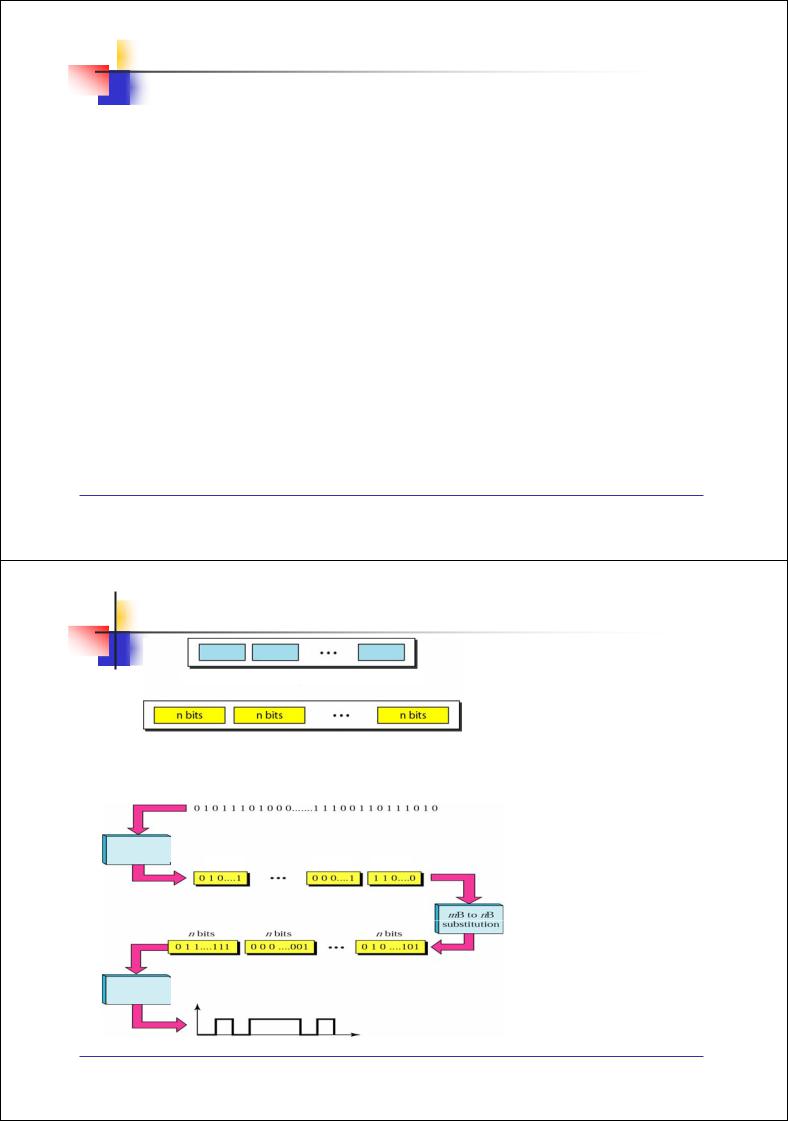
Рис. 3.8. Обнаружение ошибок в процессе блочного кодирования
Если кодовое слово не приеме принадлежит одной из разрешенных комбинаций, то оно принимается, в противном случае кодовое слово отбрасывается
Лекция 6. Обнаружение и исправление ошибок |
12 |
|
|
|
|
|
2. Блочноекодирование |
|
|
|
|
||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
Обнаружениеошибок |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пример2 |
|
|
Запрещенная |
||||||||
|
|
|
|
|
|
|
|
|
|||
Примем k = 2 и n = 3: |
Табл. 3.1 |
|
комбинация |
||||||||
|
|
|
|
|
|
|
Кодирование для обнаружения ошибок |
|
(обнаружение |
||
|
|
|
|
|
|
|
|
|
|
ошибки) |
|
|
|
|
|
|
|
Информационное слово |
Кодовое слово |
|
|
|
|
|
|
|
|
|
|
|
111 |
|
|
||
|
00 |
000 |
|
|
|
||||||
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
01 |
011 |
011 |
|
Верно |
||||||
10 |
101 |
000 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||
11 |
110 |
|
|
||||||||
|
|
|
|
||||||||
Разрешенная
комбинация
Пусть инф. слово 01 кодируется в кодовое слово 011, рассм. три случая: (ложный прием)
1.Получатель принимает 011, что является верным, и извлекает из него информационных код 01
2.Кодовое слово искажается и принимается комбинация 111 (бит слева искажен). Такой разрешенной комбинации не существует и код отбрасывается
3.Кодовое слово искажается и принимается комбинация 000 (два бита справа искажены). Извлекается неверное информационное слово 00
Лекция 6. Обнаружение и исправление ошибок |
13 |
 2. Блочноекодирование
2. Блочноекодирование
Исправлениеошибок
Для исправления ошибок требуется определить, какая конкретно комбинация передавалась
Требуется больше избыточных бит и схема кодирования
Пример3 |
|
|
|
Примем k = 2 и n = 5: |
Табл. 3.2 |
|
|
|
|
|
|
|
|
Кодирование для исправления ошибок |
Запрещенная |
|
|
|
|
|
Информационное слово |
Кодовое слово |
|
|
комбинация |
||
|
|
|
|
|
00 |
00000 |
|
|
|
|
01001 |
|
01 |
01011 |
|
|
10 |
10101 |
|
|
|
|
|
|
11 |
11110 |
|
|
|
|
|
Пусть информационное слово 01 кодируется в кодовое слово 01011:
Второй бит справа искажается, принимается комбинация 01001
Принятое слово 01001 сравнивается со всеми разрешенными и определяется количество различных бит
Комбинация отличающаяся не более чем на один бит – верная (01011)
Лекция 6. Обнаружение и исправление ошибок |
14 |

 2. Блочноекодирование
2. Блочноекодирование
РасстояниеХэмминга
Расстояние Хэмминга: определяется количеством различий между соответствующими битами в словах
Обозначается d(x, y), x и y – слова одинаковой длины
Определяется операцией XOR ( ) над двумя словами и подсчетом количества единиц в результате
Вес кодового слова: это количество единиц в кодовом слове
Расстояние Хэмминга между двумя словами определяется как количество различий между одноименными битами (вес результата XOR)
Пример4
Расстояние Хэмминга между словами:
Расстояние Хэмминга d(000, 011) равно 2, так как 000 011 = 011 (два единичных символа в слове).
Расстояние Хэмминга d(10101, 11110) равно 3, так как 10101 11110 = 01011 (три единичных символа в слове).
Лекция 6. Обнаружение и исправление ошибок |
15 |
 2. Блочноекодирование
2. Блочноекодирование
МинимальноерасстояниеХэмминга
Минимальное расстояние Хэмминга dmin: определяется как наименьшее расстояние Хэмминга между всеми возможными парами комбинаций кода
Минимальное расстояние Хэмминга определяется как наименьшее расстояние Хэмминга между всеми возможными парами на множестве комбинаций кода
Пример5 |
Информационное слово |
Кодовое слово |
Найти минимальное расстояние Хэмминга для |
00 |
000 |
кода из таблицы: |
|
|
01 |
011 |
|
|
10 |
101 |
|
|
|
|
11 |
110 |
|
|
|
Решение
Находим расстояния Хэмминга между всеми парами комбинаций в слове : |
|
|||
|
d(000, 011) = 2; |
d(000, 101) = 2; |
d(000, 110) = 2; |
|
|
d(011, 101) = 2; |
d(011, 110) = 2; |
d(101, 110) = 2; |
|
|
dmin = 2 |
|
|
|
|
|
|
|
|
|
|
Лекция 6. Обнаружение и исправление ошибок |
16 |
|

 2. Блочноекодирование
2. Блочноекодирование
МинимальноерасстояниеХэмминга
Пример6 |
Информационное слово |
Кодовое слово |
|
00 |
00000 |
||
Найти минимальное расстояние Хэмминга |
|||
01 |
01011 |
||
для кода из таблицы: |
|||
|
10 |
10101 |
|
Решение |
11 |
11110 |
|
|
|
||
|
|
Находим все возможные расстояния Хэмминга для кода из табл.:
|
d(00000, 01011) = 3; |
d(00000, 10101) = 3; |
d(00000, 11110) = 4; |
|
d(01011, 10101) = 4; |
d(01011, 11110) = 3; |
d(10101, 11110) = 3; |
|
dmin = 3 |
|
|
Три основных параметра кодирования: длина кодового слова n; длина информационного слова k; минимальное расстояние Хэмминга dmin
Форма записи схемы кодирования: C(n, k) с dmin
Примеры записи: для Примера 5: C(3, 2) с dmin = 2;
для Примера 6: C(5, 2) с dmin = 3
Лекция 6. Обнаружение и исправление ошибок |
17 |
 2. Блочноекодирование
2. Блочноекодирование
МинимальноерасстояниеХэмминга
Связь корректирующей способности кода с расстоянием Хэмминга
Расстояние Хэмминга между принятым и переданным кодовыми словами точно соответствует количеству искаженных бит
Например, передается 00000, а принимается 01101. Три бита искажены и расстояние Хэмминга равно d(00000, 01101) = 3
Минимальное расстояние Хэмминга при обнаруженииошибок
При необходимости обнаружения вплоть до to ошибок минимальное расстояние между разрешенными кодовыми словами должно быть dmin ≥ to + 1. В этом случае ошибки в кодовом слове не приводят к его трансформации в одну из разрешенных комбинаций, т.к. их не достаточно
Условие dmin ≥ to + 1 дает гарантированное обнаружение вплоть до to ошибок в слове
Если ошибок в принимаемом слове больше to, то они также могут быть обнаружены но не гарантированно (не для всех комбинаций)
Для гарантированного обнаружения вплоть до s ошибок в кодовом слове минимальное расстояние Хэмминга должно быть dmin ≥ to + 1
Лекция 6. Обнаружение и исправление ошибок |
18 |

 2. Блочноекодирование
2. Блочноекодирование
МинимальноерасстояниеХэмминга
Пример7
Минимальное расстояние Хэмминга для кода из таблицы равно 2
Гарантируется обнаружение только одной ошибки
При двух ошибках возможен переход в другую разрешенную комбинацию
Пример8
Минимальное расстояние Хэмминга для кода из таблицы равно 3
Гарантируется обнаружение до двух ошибок, т.к. любые две ошибки создают запрещенную комбинацию
Некоторые комбинации трех ошибок создают разрешенную комбинацию (ошибки не обнаруживаются)
Информационное |
Кодовое слово |
|
слово |
|
|
00 |
000 |
|
|
|
|
01 |
011 |
|
|
|
|
10 |
101 |
|
|
|
|
11 |
110 |
|
|
|
|
|
|
|
Информационное |
Кодовое слово |
|
слово |
|
|
00 |
00000 |
|
|
|
|
01 |
01011 |
|
|
|
|
10 |
10101 |
|
|
|
|
11 |
11110 |
|
|
|
|
Лекция 6. Обнаружение и исправление ошибок |
19 |
 2. Блочноекодирование
2. Блочноекодирование
МинимальноерасстояниеХэмминга
Принцип обнаружения ошибок можно посредством геометрического представления расстояния Хэмминга
|
|
Обозначения |
|
|
|
|
|
|
|
|
|
Радиус to |
|
Любое разрешенное слово |
|||
|
|
|
|
|
|
|
|
|
|||
|
|
Любое запрещенное слово с |
|||
|
|
|
количеством ошибок от 1 до to |
||
dmin > to
Рис. 3.9. Обнаружение ошибок в процессе блочного кодирования
Если передаваемое кодовое слово x представить как центр окружности с радиусом to, то все принимаемые кодовые слова с количеством ошибок от 1 до to можно представить в виде точек в пределах круга и на линии окружности (пространства запрещенных комбинаций). Все остальные (разрешенные кодовые комбинации) должны находиться вне круга
Лекция 6. Обнаружение и исправление ошибок |
20 |
