Примеры, иллюстрирующие элементы выполнения РГР2

Пример 1. Кривошип ОА длиной вращается равномерно с угловой скоростью и приводит в движение шатун АВ длиной . Найти угловую скорость и угловое ускорение шатуна, а также ускорение ползуна В при и (Рис.1).

VB AB B  P  A OA  O  Рис. 1

Решение. Модуль скорости точки А равен . С другой стороны, скорость этой же точки, считая ее принадлежащей шатуну АВ с мгновенным центром скоростей Р, можно определить так: . Отсюда величина угловой скорости шатуна .

Представим ускорение ползуна В, направленное вдоль направляющей, в виде

,

где

,

,

и поэтому

.

Модуль ускорения точки А равен

.

Далее,

; ,

где пока не известно.

Спроектируем обе части векторного равенства на оси и :

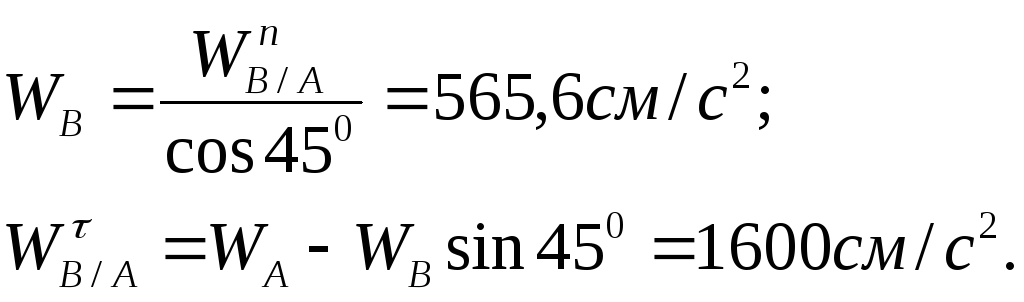
Величина углового ускорения шатуна

Пример 2. Стержень ОА механизма (Рис.2,а) вращается с постоянной угловой скоростью . Определить угловую скорость, угловое ускорение стержня АВ, а также ускорение шарнира В в положении, указанном на рисунке, если .

Y B 600 VA A 300   CB O O C a) Рис. 2

B D б)

Решение. Как и в предыдущей задаче, , .

Мгновенный центр скоростей звена АВ находится в бесконечности, т.е. . Поэтому величина угловой скорости звена . Не следует при этом делать ошибочного вывода и считать, что угловое ускорение этого звена также равно нулю. Как увидим ниже, оно существует и отлично от нуля.

Приняв за полюс точку А, представим ускорение точки В в обычном виде:

. (а)

Особенность определения ускорения состоит в том, что этот вектор не известен ни по направлению, ни по модулю. Вместе с тем, пока не может быть найден и модуль вектора , так как неизвестно угловое ускорение звена АВ. Поэтому одного векторного равенства недостаточно для определения искомого ускорения. Следует учесть, что точка В одновременно принадлежит и звену СВ и ее ускорение при вращении вокруг неподвижного центра С выражается так:

. (b)

В силу того, что угловое ускорение звена СВ пока неизвестно, модуль вектора касательного ускорения также неизвестен.

Сравнивая равенства (а) и (b), получим:

. (с)

Направление всех векторов равенства (в) указаны на Рис. 30,а.

Поскольку мгновенный центр скоростей звена АВ находится в бесконечности и поэтому , , то величина угловой скорости звена СВ будет равна

.

Модули нормальных ускорений равны

, .

Представим векторное равенство (а) графически. От произвольной точки В отложим вектор в выбранном масштабе (Рис.2,б). От конца этого вектора проведем прямую, параллельную вектору . Поскольку модуль этого вектора неизвестен, а также неизвестно направление искомого вектора , то процесс построения многоугольника ускорений применением только одного векторного равенства (а) обрывается. Это указывает на необходимость применения еще одного векторного равенства, т.е. равенства (b). Поэтому из той же точки В построим вектор . Затем от его конца проведем прямую, параллельную вектору .Точка пересечения D последней прямой с прямой, параллельной вектору , определяет конец искомого вектора . Одновременно определены и векторы , .

Выполним расчет этих ускорений методом проекций. Для этого спроектируем равенство (с) на соответствующим образом выбранные оси. Иначе говоря, каждую ось выберем так, чтобы проекция одного из неизвестных по модулю векторов или на эту ось равнялась нулю. Такими осями (Рис.2,а) являются и .

Итак,

,

.

Отсюда получим

;

.

Знак “минус” в ответе указывает на то, что вектор имеет направление, противоположное принятому на Рис.2,а.

Угловые ускорения звеньев АВ и СВ равны

, .

Направление векторов и легко установить по направлениям ускорений и . Оба вектора направлены на наблюдателя.