matan_belaev_1

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Харьковский Национальный Университет им. В. Н. Каразина

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

xk xk xn 1 , x0 = 0.

.1.pdf

Скачиваний:

Добавлен:

23.02.2015

Размер:

4.45 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 187 8 9 10 11 12 13 14 15 16 17 18 > Следующая >>>

(x)

f (x)

g ( x)

h ( x)

f (x)

g (x)

h (x)

(x)

...

(x) (x)

...

f (x)

g(x)

h( x)

f (x)

g(x)

h(x)

Если при этом (x), (x),..., (x)

также функции от x , то

f (x)

g (x)

h (x)

(x) (x) (x)

(x)

... ( x)

f (x)

' g(x)

' h(x)

(x) (x)ln f (x) (x)ln g(x) ...

(x)ln h(x) .

Этот прием нахождения производных в случае произведения ( или частного) называется взятием логарифмической производной и может быть, в некоторых случаях, весьма эффективным.

§. ВЫСШИЕ ПРОИЗВОДНЫЕ СЛОЖНЫХ ФУНКЦИЙ

Пусть Тогда

z (x)

z f (g(x)) ( f

g)(x) F(x) .

(x) z

(x)

(x) zy ( y) yx (x);

( y) yx

( y) y

z 3 ( y) y 3

(x) z 2 ( y) 2 y

(x) y 2 (x) z 2

( y) y

(x) y 2 (x) z

( y) y 3 (x) .

Пусть функции f ( y) и g(x) – n-кратно дифференцируемы в точках g(x) и х соответственно. Тогда их суперпозиция ( f g)(x) тоже n –кратно дифференцируема в точке х и ее n-я производная полиноминально выражается через значения n первых

производных функций f ( y)	и g(x) в т. g(x) и х соответственно.
§. ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ
dy df (x, dx) f (x)dx	d n y d n f (x, dx) f (n) (x)(dx)n	f (n ) (x)	d n f

dxn

d n ( f (x) g(x), dx) d n f (x, dx) d n g(x, dx)

d n ( f (x)g(x), dx) Cknd k f (x, dx)d n k g(x, dx) .

k 0

Последняя из написанных формул это формула Лейбница для высших дифференциалов функций, представленных в виде произведения.

§. ВЫСШИЕ ПРОИЗВОДНЫЕ ФУНКЦИЙ ЗАДАННЫХ ПАРАМЕТРИЧЕСКИ

x (t)

t 1 (x)

1 (x)

x 1

y (t)

y (

(x))

(x) f (x)

y 2

t x

t	1	t
t
	t	t

t2 t t t2t 3

Если из двух функций заданных и непрерывных на промежутке одна строго монотонна в окрестности точки t0 , обе дифференцируемы n-кратно в окрестности этой точки и первая производная строго монотонной функции не равна нулю то в некоторой окрестности t0 существует функция, заданная параметрически, тоже n-кратно

дифференцируемая и ее n-я производная рационально выражается через n первых производных функций и .

§. ВЫСШИЕ ПРОИЗВОДНЫЕ ОБРАТНЫХ ФУНКЦИЙ

Пусть y f (x) непрерывна, строго монотонна в окрестности т. x0 , где она n - кратно дифференцируема, причем f (x0 ) 0 . Тогда в окрестности точки y0 f (x0 ) существует

обратная функция x f 1 ( y) , которая непрерывна и строго монотонна в этой окрестности и n – кратно дифференцируема, причем n-я производная обратной функции рационально выражается через n первых производных исходной функции в т. x0 , при этом в знаменателе стоит f (x) .

;

x 2

y 2

.......................

y 2

;

( y )2 y

( y )3

y 2

y 3

yx2

3 yx

yx2

yx3

§. ИНВАРИАНТНОСТЬ ФОРМЫ ПЕРВОГО ДИФФЕРЕНЦИАЛА И НЕИНВАРИАНТНОСТЬ ФОРМЫ ВЫСШИХ ДИФФЕРЕНЦИАЛОВ ФУНКЦИИ

Пусть y f g x . Тогда

dy(x)

dy y (x)dx

y	(x)dx f (g)g		(x)dx f (g)dg	т.е.
x	g	x	g

и dy y (g)dg .

Здесь – независимая переменная, а g – функция зависящая от х.

И, тем не менее, формулы для нахождения первого дифференциала одинаковы.

Это явление выражает инвариантность формы первого дифференциала относительно замены переменных.

Теперь для независимой переменной х

d 2 y(x) d (dy(x)) d ( y	(x)dx) dy	(x)dx y	(x)d (dx) =
x	x	x

=	y 2 (x)dxdx y		(x)d 2 x y 2 (x)dx2 y (x)d 2 x .
	x	x		x	x
	x			x
А для зависимой переменной g
d 2 y(g) d ( y dy) dy (g)dy y				(g)d (dg) y 2	(g)(dg)2 y	(g)d 2 g .
g	g		g	g	g
				g
Получили:
d 2 y(x) y 2 (x)dx2 ,				если х – независимая переменная, и
x
d 2 y(g) y 2	(g)dg2 y	(g)d 2 g		, если g – зависимая переменная т.е. функция.
g	g
g
Это и есть не инвариантность формы второго (и, естественно, более высоких)
дифференциала относительно замены переменных.

РАЗДЕЛ. ОСНОВНЫЕ ТЕОРЕМЫ О ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ

Функция называется возрастающей в некоторой окрестности U x точки x0 , если
			0
x Ux	f (x) f (x0 )	0 .

0	x x0

Функция называется убывающей в некоторой окрестности U x			точки x0 , если
	0

x Ux	f (x) f (x0 )	0 .

0	x x0

Если функция дифференцируема в точке и ее производная больше (меньше) нуля, то она возрастает (убывает) в этой точке.

т.е.	f (x ) lim		f (x) f (x0 )	0	U		x U		f (x) f (x0 )	0
т.е.	f (x ) lim			0	U	x	x U	x		0
	x 0		x x0			x		x	x x0
		x x0	x x0			0		0	x x0
						0		0

а это и есть возрастание функции, имеющей положительную производную. Аналогично для убывания функции, имеющей отрицательную производную.

Пусть sup E( f ) M;	inf E( f ) m .
Если для значений M и m справедливо, что
xM D( f )	f (xM ) M и	xm D( f )	f (xm ) m ,
xM D( f )	f (xM ) M и	xm D( f )	f (xm ) m ,

то говорят, что достигаются максимальное и минимальное значения функции, и они

обозначаются	M	max f (x);	m min f (x) .
Пусть M max f (x);		m min f (x) . Тогда

Если это справедливо на всей области определения D( f ) функции f (x) , то

говорят, что это глобальный максимум и глобальный минимум.

Если это справедливо на некотором подмножестве D( f ) мы имеет место локальный максимум и локальный минимум.

Строгий максимум, если	x D( f ), x xM		f (x) f (xM )
не строгий максимум, если	x D( f ), x xM		f (x) f (xM )

аналогично определяются строгий минимум и нестрогий минимум.

Точки максимума и минимума называются точками экстремума.

Внутренний экстремум – достигается внутри D( f ) .

Краевой экстремум – в граничной точке D( f ) .

Т (Ферма). В точке локального внутреннего экстремума производная функции, если она существует и конечна, равна нулю.

∆(для max). Пусть функция

f (x) в точке xM имеет локальный внутренний максимум.

Тогда :

x Ux

D( f ),

f (x) f (xM )

sign(xM x) .

x xM

Получаем :

f (x

)

lim

f (x) f (xM )

0 и

f (x

) lim

f (x) f (xM )

f (x ) 0 . ▲

x xM 0

x x

x xM 0

x x

Т (Ролля). Если функция f (x) дифференцируема внутри замкнутого промежутка и

непрерывна на нем, причем на концах промежутка, принимает равные значения, то внутри промежутка найдется точка с нулевой производной (хотя бы одна).

	f (x) C			f (x) C1	f (a) f (b)			f () 0 .

		a,b		a,b

∆. Функция непрерывная на замкнутом промежутке							необходимо ограничена на нем т.е.
	m, M			m f (x) M		причем m, M – достигаются. Возможны два случая:

a)	m M		f (x) const			f (x) 0 .
b)	m M		существует хотя бы один внутренний локальный экстремум.

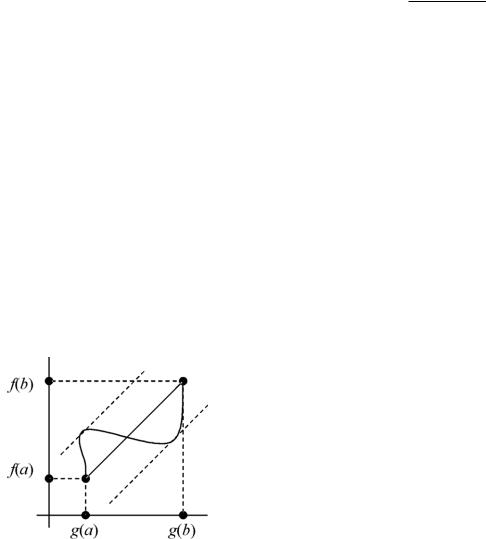
Следовательно, по теореме Ферма, a,b

		f ( ) 0 . ▲

Т (Лангранжа). Если функция непрерывна на замкнутом промежутке и дифференцируема внутри него то внутри промежутка есть точка, в которой касательная параллельна хорде, соединяющей точки (a, f (a)) и (b, f (b)) .

∆ Рассмотрим F(x) f (x) Lx , где L некоторая постоянная.

По условию теоремы F (x) - непрерывна на [a,b], дифференцируема на (a,b) .

Константу L подберем из условия : F(a) = F(b). Получим:

f (a) + La = f (b) + Lb, f (a) – f (b) = L(b-a) L f (b) f (a) . b a

Так построенная функция F (x) f (x)

f (b) f (a)

x удовлетворяет условиям теоремы

b a

Ролля . Значит

a,b

f (b) f (a)

F ( ) 0

f ( )

b a

т.е.

f ( )

f (b) f (a)

. ▲

b a

Следствие: Если

f (x) на (x, x x) дифференцируема, то

(x, x x)

f (x x) f (x)

f ( )

f (x x) f (x) f ( ) x

x x

(0 1)

f (x, x) f (x x) f (x) f ( ) x

x x

(0 1)

Полученная формула называется формулой конечных приращений.

Tº (Формула Коши). Если две функции непрерывны на замкнутом промежутке дифференцируемы внутри него и:

их производные одновременно не равны 0;

значения одной из функций на концах промежутка не совпадают;

то внутри промежутка есть точка где касательная к
кривой, заданной параметрическими уравнениями,
определяемыми этими функциями параллельна хорде.
f (t), g(t) C a,b		f (t), g(t) C a,b		f´²(t) + g´²(t) ≠ 0

( f(a) ≠ f(b) g(a) g(f) )
(a, b)	f b f a	f
			.
	g b g a	g

∆ Пусть g(a) g(b) .

Рассмотрим функцию F(x) = f (x) – Lg(x) . Эта функция F(x) = f (x) – Lg(x) непрерывна на [a,b] и дифференцируема на (a,b).

Потребуем: F(а) = F(b)	f (а) – Lg(а) = f (b) – Lg(b) . Тогда		L=	f (b) f (a)	0 и по
				g(b) g(a)

теореме Ролля :	F ( ) 0	f (t) Lg (t) 0 при t =

F (a) f (a) 0 F (b) f (b) 0 .

L	f ( )	f ( )	f (b) f (a)	. ▲
	g ( )	g ( )	g(b) g(a)

Tº (Дарбу). Произвольная функция, дифференцируемая на замкнутом промежутке, и принимающая два некоторых значения принимает и всякое промежуточное значение.

Частный случай : Если на концах промежутка функция имеет производную разных знаков, то внутри промежутка есть точка, в которой производная равна нулю.

∆ Пусть f (a) f (b) и γ ( , β).

Рассмотрим функцию F(x) = f (x) – γx. Для неѐ

F (x) на концах промежутка принимает значения разных знаков, следовательно

F ( ) f ( ) 0	f ( ) .	▲

Tº (Об односторонней производной). Если функция f определена в односторонней окрестности точки x = a и непрерывна в ней , а в соответствующей проколотой окрестности дифференцируема, то односторонняя производная равна соответствующему

пределу производной в этой точки

(a)

lim f (x) .

x a 0

∆ Пусть

Тогда

a, x

f (x) f (a)

x Ua

x a

f (x) .

Т.к.

a <

γ(x)

< x , то

lim (x) a .

x a

Если в формуле

f (x) f (a)

f '( (x))

устремить x → a + 0, то получим

x a

f (a)

lim

f (x) f (a)

▲

x a 0

x a

§. ФОРМУЛА И МНОГОЧЛЕН ТЕЙЛОРА

Пусть f (x) – n-кратно дифференцируема в т. х0. Полиномом Тейлора этой функции называется

n	f k (x )		k					f n x0 x x0	n
Pn f , x0 ; x	0	x x0		f x0	f ' x0	x x0	...			.
Pn f , x0 ; x	k !	x x0		f x0	f ' x0	x x0	...	n!		.
k 0	k !							n!

Все производные Pn (f, x0; x) от нулевой до n-ной совпадают с соответствующей функцией f (x). Разность между функцией f (x) и ее полиномом Тейлора называется остаточным членом формулы Тейлора

Rn (f, x0; x) f (x) – Pn (f, x0; x) ,

А представление f (x) Pn (f, x0; x) + Rn (f, x0; x) называется формулой Тейлора для функции f (x) в окрестности точки x0. При этом все производные остаточного члена Rn (f, x0; x) от нулевой до n-ной равны 0 в т. х0.

§ ФОРМУЛА ТЕЙЛОРА С ОСТАТОЧНЫМ ЧЛЕНОМ В ФОРМЕ ПЕАНО

Записывая в формуле Тейлора, вместо остаточного члена, его выражение, полученное Пеано, получим формулу Тейлора с остаточным членом в форме Пеано.

(x0 )

f x Pn f , x0 , x Rn f , x0 ; x

Rn f , x0 ; x

k 0

k !

f 2 (x0 )

f n (x0 )

f (x0 ) f

(x0 ) x x0

(x x0 )

...

(x x0 )

Rn f , x0

; x

f 2 (x0 )

f n (x0 )

f (x0 ) f

(x0 ) x x0

(x x0 )

...

(x x0 )

((x x0 )

)

Остаточный член формулы Тейлора в форме Пеано дает возможность положительно ответить на вопрос, будет ли уменьшаться остаточный член формулы Тейлора с увеличением степени полинома Тейлора.

Однако остаточный член формулы Тейлора в форме Пеано не дает возможности количественно оценить ошибку замены функции полиномом Тейлора.

§ ОСТАТОЧНЫЙ ЧЛЕН В ФОРМЕ ШЛЁМИЛЬХА – РОША

Для функции f (x) n раз дифференцируемой на промежутке с концами х и х0 и (n+1) раз дифференцируемой внутри него и для любой функции (x) заданной на промежутке с концами х и х0, дифференцируемой внутри него, имеющей ненулевую производную

( (x) 0 ) имеет место формула:

Rn f , x0 ; x

f n 1

x x

В этой формуле = х0

+ (х – х0), 0

< < 1, |x – x0| > | – x0| > 0.

Рассмотрим

F t f x Pn f ,t; x f x f

t x t k .

k 0

k !

F t f

k 1

t x t k f

t k x t k 1 1 =

k 0

k !

k 0

k !

k 1

x t k

x t k 1

. Во второй сумме положим k = l + 1.

k 0

k !

k 1

k !

x t l

x t

n .

F t = f

k 1

x t k

l 1

k 1

n 1

k 0

k !

l 0

l 1 !

Тогда по формуле Коши получаем:

F x

F '

f l 1 x n

n! '

F x F x0

Rn f , x0 , x

Учитывая, что

x x

получаем:

f , x ; x

f k 1 x n

x x

. ▲

n! ' x

Получен остаточный член в форме Шлѐмильха – Роша.

	§ ОСТАТОЧНЫЙ ЧЛЕН В ФОРМЕ ЛАГРАНЖА
В остаточном члене в форме Шлѐмильха – Роша положим		(t) = (x - t)n+1;
	n	n+1	. Получаем
Тогда (t) = – (n + 1)(x - t) . Причем (x) = 0, (x0) = (x – x0)

R f , x ; x		f n 1 x	x x	n 1 ,	где x	x x , 0 < < 1.
		n 1 !
n	0		0		0	0

Получен остаточный член ряда Тейлора членом в форме Лагранжа.

§ ОСТАТОЧНЫЙ ЧЛЕН В ФОРМЕ КОШИ

Полагая (t) = x – t и учитывая, что (x0) = x – x0, (x) = 0, (t) 1 получим остаточный член ряда Тейлора членом в форме Коши:

R	f , x ; x	f n 1	x	n	x x	, где	= x0 + (x – x0) ,	0 < < 1.
R	f , x ; x		x		x x	, где	= x0 + (x – x0) ,	0 < < 1.
n	0	n!			0
		n!

§ ТЕОРЕМА ЕДИНСТВЕННОСТИ

Т˚. Разложение функции в ряд Тейлора в окрестности заданной точки х0 единственно с точностью до порядка следования слагаемых, т.е. в асимптотическом разложении

функции f (x) по системе степенных функций

(x) (x x )n :

k x x0 n

f x

x x0

при х х0

k 0

f k x

коэффициенты Сk находятся однозначно и, при этом Ck

§ ФОРМУЛА ТЕЙЛОРА ДЛЯ f (x) В ТЕРМИНАХ ДИФФЕРЕНЦИАЛОВ

Формула Тейлора с остаточным членом в форме Лагранжа

f k x

f n 1

n 1

f x

x x0

, где x0 x x0 ,

0,1 может

k !

1 !

k 0

быть записана в терминах дифференциалов:

f x

d k

f x0 , x

d k 1 f , x .

k 0

k !

1 !

§ПЯТЬ ЗАМЕЧАТЕЛЬНЫХ РАЗЛОЖЕНИЙ ФУНКЦИЙ В РЯД ТЕЙЛОРА

ВОКРЕСТНОСТИ ТОЧКИ x0 = 0.

Разложения функций в ряд Тейлора в окрестности точки x0 = 0 называются разложениями в ряды Маклорена.

Множество значений х при которых ряд сходится называется областью сходимости


ряда. Степенной ряд вида	f x ck x x0	k	сходится в интервале x R, x R
	k 0		0	0
	k 0

и R называется радиусом сходимости степенного ряда. В точках x0 R и x0 R ряд может, как сходиться, так и расходиться. Радиус сходимости степенного ряда может быть

найден по формулам: R lim	ck		(формула Даламбера) или R lim	1		(формула
	c
	c	1		k c
	k	1			k

Коши). По другому область сходимости ряда может быть установлена при оценке остаточного члена.

Более подробные сведения о рядах будут рассматриваться в последующем курсе.

Ниже следующие разложения получены по общей формуле разложения функции в ряд Тейлора.

			n	n		k
1 .	ex	x			x		xk 1	(x0 = 0);
		n!
	k 0			k 0	k !

Оценим остаточный член, записав его в форме Лагранжа:

R exp, 0; x

xn 1

n 1 .

n 1 !

Из оценки следует, что при любом фиксированном х и n стремящемся к бесконечности остаточный член стремится к нулю, т.е. ряд сходится для любых х.

Тот же результат может быть получен из формулы Даламбера:

n 1

R lim

lim

n 1 !

lim

xn 1

n 1

Область сходимости

ряда х (– ; + ).

2n 1

2k 1

x2n 3 , (x0 = 0).

2 .

sin x

...

2n 1 !

2k 1 !

n 0

3! 5!

k 0

Оценка для остаточного члена:

				2n 3

			sin
	R	sin, 0; x			2	x2n 3
					2
				2n 3 !
	2n 1


Область сходимости ряда х (– ; + )

x 2n 3

2n 3 ! 0n .

3 .

cos x

...

x2k 2

, (x0 = 0).

2n !

2k !

n 0

2! 4!

k 0

Оценка остаточного члена:

2n 2

cos

2n 2

cos, 0; x

x2n 2

2n 2 !

n .

2n 1

Область сходимости ряда х (– ; + ).

4 .

ln 1 x 1

n 1

x x

...

n 1

xn 1

, (x0 = 0).

n 1

Оценка остаточного члена:

R ln, 0; x

1 n n! x n x

n 1

n .

1 n 1 n!

n 1

Если х = 1, то получается ряд ln 2 1

, который сходится по признаку Лейбница.

n 1

Область сходимости ряда х (-1, 1].

5 .

1 x 1 ...

n 1 xn 1 ... n 1 xn (xn 1 ) ,

n 0

(x0 = 0).

Для остаточного члена получаем:

Rn 1 x , 0;1

1 ... n 1 n 1

x n x

1 ... n

n 1 1 sgn 1

n 1

1 ... n

xn 1 0n .

если

Область сходимости:

1) N, x (–; +);

2) > 0, x [–1; 1] ;

3) (–1, 0), x (–1; 1] ;

4) Общ. случай

x (–1; 1).

§ ЕЩЕ НЕСКОЛЬКО ПОЛЕЗНЫХ РАЗЛОЖЕНИЙ.

6 .

1 x 1

1 x

x 2 x3

... 1 n x n

...

x0 = 0

1 x

1 x 1

1 k xk 1 k xk xn 1 .

1 x

k 0

Может быть получено из формулы для суммы бесконечно убывающей геометрической прогрессии или из известного разложения 1 x .

Область сходимости ряда x (–1, 1).

Получено из формулы для суммы бесконечно убывающей геометрической прогрессии. Область сходимости: x (–1, 1).

n 1

3 !!x n ;

2n 1 !!x n

8 .

x 1

x [–1, 1].

2n !!

1 x

n 0

2n !!

При этом: (2n)!! = 2 4 6 ... (2n);

(2n+1)!! = 1 3 5 … (2n + 1).

0!! 1;

(–1)!! 1;

(–3)!! – 1.

(2n + 1)! = (2n + 1)!! (2n)!! = (2n + 1)!! n! 2n.

9 .

10 .

11 .

f x arctgx

f ' x

1 x2 x4

....

2k 1

f x x

... 1 k

, (|x| < 1).

2k 1

k 0

1 2n 1 !!

2n 1 !! x2n , (|x| < 1).

1 x2

2n !!

n 0

2n 2

f x arcsin x f ' x

arcsin x 2n 1 !!

, (|x| < 1).

2n 1

1 x2

n 0

2n !!

РАЗДЕЛ. ИЗУЧЕНИЕ СВОЙСТВ ФУНКЦИЙ С ПОМОЩЬЮ ПРОИЗВОДНЫХ

§ НЕОБХОДИМОЕ И ДОСТАТОЧНОЕ УСЛОВИЕ ПОСТОЯНСТВА ФУНКЦИИ, ДИФФЕРЕНЦИРУЕМОЙ НА ПРОМЕЖУТКЕ.

Т. Функция f (x) непрерывная на [a,b] и дифференцируемая на (a,b) постоянна тогда и только тогда когда ее производная равна нулю.

1) f (x) = const		f (x) 0 .
2)		f x1 f x2	f ,	x1 x2 (по теореме Лагранжа)

	f (x) 0	x1 x2
		x1 x2

f (x1) – f (x2) = (x1 – x2) f ( ) = 0 f (x1) = f (x2). ▲

§ УСЛОВИЕ НЕУБЫВАНИЯ (НЕВОЗРАСТАНИЯ) ФУНКЦИИ.

Т. Функция не убывает, когда ее производная не положительна. Функция не возрастает, когда ее производная не отрицательна.

Докажем для не убывающей функции.

1) f (x) - не убывает			x1, x2		f x1 f x2		0	f ' x	0 .
1) f (x) - не убывает			x1, x2				0	f ' x	0 .
					x1 x2			1
					x1 x2
2)		f	x1 f x2	f ' 0		f (x) не убывает. ▲

	f (x) 0		x1 x2
			x1 x2

§ УСЛОВИЕ СТРОГОЙ МОНОТОННОСТИ ФУНКЦИИ.

Т. Функция строго монотонна тогда и только тогда когда ее производная внутри промежутка не меняя знака, обращается в ноль не более чем на множестве без внутренних точек.

Допустим f (x) не убывает и не является строго возрастающей. Тогда

<<< < Предыдущая 1 2 3 4 5 67 / 187 8 9 10 11 12 13 14 15 16 17 18 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
14.11.2019428.03 Кб2Maket_tablits.doc
#
23.02.2015249.34 Кб4marketing (Автосохраненный).doc
#
23.02.201563.45 Кб16MARKETING-2013.docx
#
17.09.201987.78 Кб5Market_issled_Iv_Roshe.docx
#
11.11.2019917.5 Кб17Masenko_Mova_i_suspilstvo_2004.doc
#
23.02.20154.45 Mб10matan_belaev_1.1.pdf
#
23.02.20151.04 Mб12matan_metod_1.1.pdf
#
23.02.20151.27 Mб37matan_metod_2012_1.2.doc
#
13.03.2016624.21 Кб4Matem_Lisitsya_2.pdf
#
23.02.20151.1 Mб13MechanS2.doc
#
23.02.20153.01 Mб30Mekhanika_metodichka.doc