matan_belaev_1

Т˚. Предел последовательности существует тогда и только тогда, когда ее верхний и нижний пределы совпадают.

U a и U b . Тогда смешав элементы этих двух последовательностей получим

последовательность, не имеющую предела. Следовательно, если верхний и нижний пределы последовательности не равны между собой, то существует подпоследовательность, не имеющая предела и, значит, предел последовательности не существует.

У всякой функции, для которой a D ( f ) , существуют наибольший и наименьший частичные пределы. Они называются верхним и нижним пределами функции f (x) при

А. Критерий Коши для последовательности.

Последовательность xn сходится тогда и только тогда, когда она фундаментальна.

В. Критерий Коши для функции.

Функция f (x) при x a , a D ( f ) имеет конечный предел тогда и только тогда, когда:

§ ТЕОРЕМА ШТОЛЬЦА

Т . Если для двух последовательностей, из которых вторая строго монотонна и неограничена существует предел отношения приращений общих членов (конечный или равный +∞, -∞), то существует и равен этому пределу предел отношения общих членов

4 . Для положительной последовательности, если существует предел отношения ее общего члена к предыдущему (конечный, равный +0, или равный +∞), то существует имеющий то же значение предел корня n-й степени из хn.

Def3. В изолированной точке области определения функция считается непрерывной, непрерывной справа и непрерывной слева.

Def Функция f (x) называется непрерывной на множестве Х, если она непрерывна в каждой точке этого множества.

Def. Функция f (x) непрерывна на [a,b], если она непрерывна x (a, b) и непрерывна справа в т. x = a, непрерывна слева в т. х = b.

Def . Функция f (x) называется кусочно-непрерывной на промежутке, если она непрерывна в каждой точке этого промежутка всюду, исключая конечное число точек этого промежутка.

§ КЛАССИФИКАЦИЯ ТОЧЕК РАЗРЫВА

Условие непрерывности функции f (x) в т. x x0

Т.к. пределы функции в точке и слева и справа существуют и конечны, то в т. x x 0 , в

Т˚. (Критерий непрерывности монотонной функции). Если значения монотонно возрастающей функции содержатся в промежутке Y и сплошь заполняют его (т.е.

f (x ) y ), то эта функция непрерывна на Х. ∆▲

§ Теорема о промежуточном значении непрерывной функции (Больцано-Коши)

Т˚. Функция, непрерывная на промежутке и принимающая какие-либо два значения, принимает и всякое промежуточное значение. (Значения, которые принимает непрерывная функция на промежутке, сами заполняют некоторый промежуток).

Пусть I – интервал; a, b [a, b] I . f (a) = α; f (b) = β.

Т˚. Непрерывная на замкнутом промежутке a,b функция f (x), на концах промежутка принимающая значение разных знаков, неминуемо внутри промежутка обращается в ноль.

∆Доказательство проведем методом вилок

Положим a1 a и b1 b . Делим отрезок [a1 , b1 ] пополам точкой с . Если f (c) 0 то теорема доказана. Если же f (c) 0 , то на одном из двух промежутков [a1 ,c] или [c,b1 ] функция имеет разные знаки на концах . Пусть это отрезок, например [a1 ,c] .

Положим a2 a1 и b2 c . Получим промежуток [a2 , b2 ] .

Продолжая эту процедуру мы либо на некотором конечном шаге найдем точку с в которой f (c) 0 , либо получим бесконечную последовательность вложенных замкнутых

промежутков, удовлетворяющих условию f (an ) f (bn ) 0 .

§ Существование экстремумов непрерывной функции на сегменте (теорема Вейерштрасса)

Построив последовательность {xn } выделим из неѐ сходящуюся последовательность

Полученное противоречие, доказывает ограниченность функции сверху. (Аналогично доказывается ограниченность функции снизу.

Последнее неравенство противоречит тому, что M sup f (x) . (аналогично с точной нижней гранью). ▲

Т . (об обратной функции). Если y = f (x) определена, монотонно возрастает (убывает) и непрерывна в некотором промежутке Х, то в соответствующем промежутке Y значений

этой функции существует однозначная обратная функция x = f 1 (y) также монотонно возрастающая (убывающая) и непрерывная.

∆ (для возрастающей функции) . Отметим, что D( f 1 ) E( f ); E( f 1 ) D( f )

1) Существование обратной функции. Если f (x) непрерывна, то еѐ значения заполняют промежуток Y сплошным образом, т.е. y0 !x 0 | f (x0 ) y0 . Единственность

такого x следует из монотонности исходной функции. Тогда : y0 x0 , т.е. x = f 1 (y) .

2)Монотонность. Пусть y // y / f (x // ) f (x / ) x // x / . Т.е. x = f 1 (y) – монотонна.

3)Непрерывность (из критерия непрерывности монотонной функции). Значения

x = f 1 (y) сплошь заполняют промежуток Х и f 1 (y) – монотонна. ▲

§ ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ

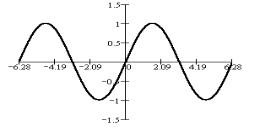
1 . y = sin x

Синусом числового аргумента называется синус угла в соответствующее число радиан. Синусом угла называется ордината конца подвижного радиуса, отвечающего

заданному углу, на тригонометрическом круге (на круге единичного радиуса).

D(sin) R E(sin) 1,1 . Функция нечетная, периодичная с

периодом Т = 2 .

Ее график приведен выше. Решение простейших уравнений

2 . y = cos x

Косинусом числового аргумента называется синус угла в соответствующее число радиан. Косинусом угла называется абсцисса конца подвижного радиуса, отвечающего заданному углу, на тригонометрическом круге (на круге единичного радиуса).

D(cos) R E (cos) 1,1 . Функция четная, периодичная с

периодом Т = 2 .

Ее график приведен выше. Решение простейших уравнений

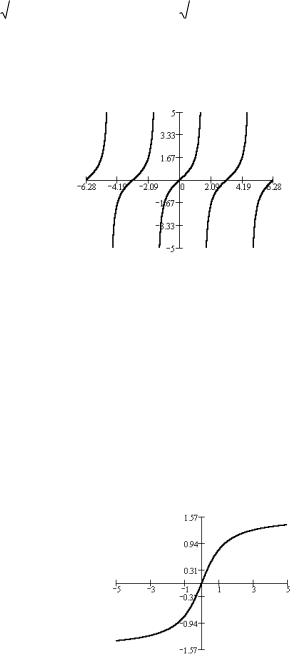
3. y = tg x

Тангенсом числового аргумента называется отношение синуса и косинуса того же аргумента. Его величина равна ординате точки пересечения продолжения радиуса подвижного круга с вертикальной прямой, проходящей через точку с координатами ( 1, 0) на тригонометрическом круге (эта прямая называется осью тангенсов).

D(tg) = R\{x x = 2 k , k Z } Е(tg) = R.

Функция нечетная, периодичная с периодом Т = . График функции приведен выше.

монотонно возрастает и непрерывна. Следовательно, существует обратная к ней функция:

y = arctg x . Справа приводим ее график.

И тогда можно решить, приведенное выше простейшее уравнение

arctg( x ) arctgx

4. y =ctg x

Котангенсом числового аргумента называется отношение косинуса и синуса того же аргумента. Его величина равна абсциссе точки пересечения продолжения радиуса круга с горизонтальной прямой, проходящей через точку с координатами ( 0, 1) на тригонометрическом круге (эта прямая называется осью котангенсов).

D(сtg) = R\{x x = k , k Z } Е(сtg) = R.

Функция нечетная, периодичная с периодом Т = . График функции приведен выше.

монотонно убывает и непрерывна. Следовательно, существует обратная к ней функция:

y = arcсtg x . Справа приводим ее график.

§ ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ.

Каждая тригонометрическая функция имеет свой гиперболический аналог.

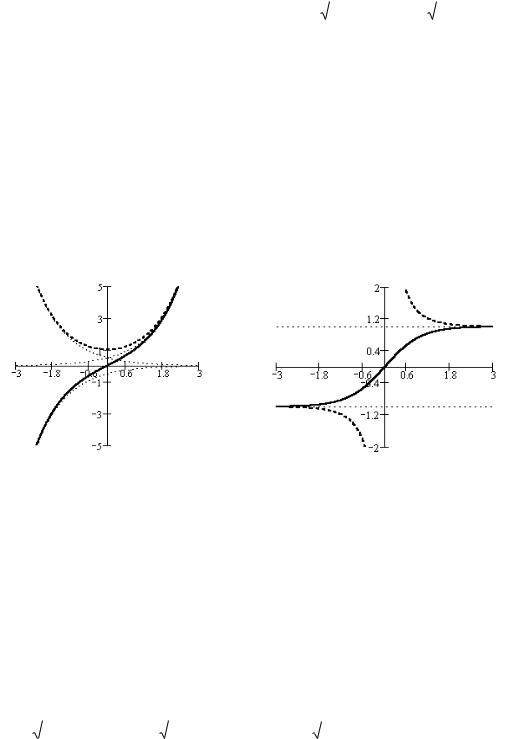
На рисунке слева приводятся графики гиперболических синуса (сплошная линия) и косинуса (пунктирная линия). Тонкой пунктирной линией построен график функции

y ex / 2 и симметричные ему относительно оси абсцисс и оси ординат.

На рисунке справа приводятся графики гиперболических тангенса (сплошная линия) и

котангенса (пунктирная линия). Тонкой пунктирной линией построен график функций y 1.