
matan_belaev_1
.1.pdf
∆ lim( f g)(x) lim( f (x) g(x)) lim |
f (x) lim g(x) f (xo ) g(x0 ) ( f g)(x0 ) . |
||
x x0 |
x x0 |
x x0 |
x x0 |
(для произведения и частного аналогично).▲
Следствия:
10.Любая натуральная степень непрерывна f (x) x непрерывна f n (x) xn . непрерывна.
n |
|
|
20.Любой многочлен Pn (x) ak xk непрерывен. |
||
k 1 |
|
|
30.Любая рациональная функция R(x) |
Pn (x) |
непрерывна в своей области определения. |
|
Qm (x) |
|
T0.Суперпозиция непрерывных функций непрерывна.
∆ Справедливость следует из теоремы о пределе сложной функции▲
§ ЧАСТИЧНЫЕ ПРЕДЕЛЫ
Def. Сужением функции на множество M или ограничением функции f (x) на множество
M называется: |
|
|
|
|
|
||
f |
|
M (x ) f (x ) |
x D( f |
|
M ) D( f ) M . |
||
|
|
||||||
Def. Частичным пределом функции |
|
f (x) по множеству M называется предел |
|||||
ограничения этой функции на множество M . |
|||||||
|
|
lim f | |
(x) |
lim f (x) . |
|||
|
|
x x0 |
|
M |
M x x0 |
||
T0. Если в точке x a существует предел функции, то в этой точке существует и равен ему всякий частичный предел, о котором имеет смысл говорить.
∆ lim f (x) b a D( f ) |
U Va |
f (Va ) U b |
f (Va M ) U b , |
||
x a |
b |
|
|
|
|
а это значит, что |
lim f |
|
M (x ) b ▲ |
|
|
|
|
||||
|
x a |
|
|
|
|
Примечание: Из существования частичного предела и, даже, бесконечного числа равных частичных пределов не следует существование предела функции.
Пример: |
lim sin x 1, |
|
|
|
, но lim sin x . |
x x | x |
2 |
2k , k Z |
|||
|
x |
|
|
x |
|
|
|
|
|
Т (об односторонних пределах). Если существуют и равны между собой оба односторонних предела, то существует и равен их общему значению предел функции в данной точке.
∆ a D( f |
|
a, ) |
) |
U |
b |
V |
x D( f ) V |
f (x ) U |
b |
, |
||||
|
||||||||||||||
|
|
|
|
|
a |
|
a |
|
|
|||||
|
|
|
|
) |
U |
|
V |
x D( f ) V |
f (x ) U |
|
|
|||
a D( f |
|
( ,a |
|
b |
b |
. |
||||||||
|
|
|
|
|
a |
|
a |
|
|
|
||||
Возьмѐм V |
V V |
|
и получим |
lim f (x ) b |
|
▲ |
||||||||
|
|
a |
|
a |
|
|
a |
|
|
x a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
§ ПРЕДЕЛЬНЫЙ ПЕРЕХОД В РАВЕНСТВАХ И НЕРАВЕНСТВАХ
10. Если функции, имеющие предел в некоторой точке совпадают на множестве сгущающемся в этой точке, то их пределы равны.
20. Если последовательности, имеющие предел, содержат совпадающие подпоследовательности, то их пределы равны.
30. Если функции совпадают в проколотой окрестности предельной точки, то их пределы равны в случае существования .
40. Если две последовательности совпадают, начиная с некоторого номера, то их пределы существуют или не существуют одновременно, и в случае существования равны.
50. Если из двух функций одна не превышает другой в проколотой окрестности предельной точки, то предел первой не превосходит предела второй в случае их существования.
60. Если предел одной функции больше предела второй в некоторой точке, то существует проколотая окрестность этой точки, в которой первая функция больше второй.
∆ 10,20: |
lim f (x) , lim g(x) |
|
и имеется множество M : |
|
|
||||||||||||||||||||
|
|
x a |
|
|
|
x a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x M f (x) g(x) a M . |
|
||||||||||||||||
|
Тогда lim f (x) lim f |
| |
|
|
(x) lim g| |
(x) lim g(x) . |
|
|
|||||||||||||||||
|
|
|
x a |
|
x a |
|
|
M |
|
|
|
x a |
|
M |
x a |
|
|
|
|||||||
30,40: Во-первых: |
|
|
|
|
|
|
|
|
|
|
|
(x ) lim f (x ) . |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
W |
a |
lim f |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
x a |
|
|
W a |
|
|
|
x a |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Во-вторых: |
lim f (x ) lim f |
|
|
(x ) lim g |
|
(x ) lim g(x ) . |
||||||||||||||||||
60: |
|
|
x a |
|
|
x a |
|
|
|
W a |
|
|
x a |
|
W a |
x a |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Пусть lim f (x) b ; |
lim g(x) c ; |
b c , тогда |
|
|
|
||||||||||||||||||||
|
|
x a |
|
|
|
|
x a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim f (x) b |
0 |
V a |
|
x Va |
b f (x) b , |
|||||||||||||||||||
|
x a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
lim g(x) c |
0 |
|
|
|
|
|
|
|
c g(x) c . |
|||||||||||||||
|
U a |
|
x U a |
||||||||||||||||||||||
|
x a |
b c ; |
W V U |
|
, |
|
|
|
|
|
|
|
|||||||||||||
Выберем |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
2 |
|
|
|
|
a |
|
|
|
|
a |
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тогда |
|
|
|
x W a |
|
|
|
g(x) c b f (x) . |
||||||||||||||
50: |
|
f (x) g(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Пусть |
x W |
a |
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Докажем, что lim f (x) lim g(x) . |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
x a |
|
|
|
|
x a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Доказательство здесь проведем от противного. |
|
|
|
|
|||||||||||||||||||||
|
|
|
lim f (x) lim g(x) , получим по п.60 |
|
f (x) g(x) , |
||||||||||||||||||||
Допустив, что |
W |
a |
|||||||||||||||||||||||
|
|
|
x a |
|
x a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
а это противоречит условию теоремы. |
|
|
|
|
|
|
▲ |
|
|
|
|||||||||||||||
и, наконец |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Т0. (Принцип двустороннего ограничения, теорема о двух милиционерах).
Если две функции имеют общий предел и в окрестности предельной точки третья функция заключена между ними, то она имеет тот же предел.
∆ следует из 50 и 60.
|
|
|
|
, |
|
Пусть |
f (x) k(x) g(x) |
x W a |
|
||
|
lim f (x) b U b |
Va |
x Va D( f ) |
f (x ) U b , |
|
|
x a |
|
|
|
|
|
lim g(x) b U b |
|
g(x ) U b |
||
|
W a |
x W a |
D(g) |
||
|
x a |
|
|
|
|
и, т.к. k(x) g(x) и k(x) f (x) ,
|
|
|
k (x ) U b |
то |
x Va |
W a D( f ) D(g) |
|
|
|
т.е. lim k(x) b . |
|
|
|
▲ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
x a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
§ НЕПРЕРЫВНОСТЬ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ |
|
|
|||||||||||||||||||||||||||||||||||||||
10. |
f (x) sin x , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
sin x sin x |
0 |
|
2 |
|
sin |
x x |
0 |
|
|
|
cos |
x x |
0 |
|
2 |
|
sin |
x x |
0 |
|
2 |
|
|
x x 0 |
|
|
|
x x |
0 |
|
. |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
2 |
|
2 |
|
|
|
2 |
|
|
2 |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Выбрав получим, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
0 0 |
( ) |
| 0 |
|
x x0 |
|
|
|
|
sin x sin x0 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
т.е. lim sin x sin x0 . |
|
|
|
Функция y sin x непрерывна x R . |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
x x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
0 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) cos x |
||||||||
|
f (x) cos x sin |
|
|
|
x -суперпозиция линейной функции и sin x , |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
непрерывна как суперпозиция двух функций непрерывных x R .
30. Функции tgx, ctgx непрерывны x R, кроме точек, в которых знаменатель обращается в ноль (как частное двух непрерывных функций),
т.е. функции y = tgx и y = ctgx непрерывны в своей области определения.
РАЗДЕЛ 5. ЗАМЕЧАТЕЛЬНЫЕ ПРЕДЕЛЫ
§ ПЕРВЫЙ ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛ
|
Рассмотрим |
0 x |
. |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда |
0 < S ∆AOB < S сек.АОВ < S ∆AOC , |
||||||||||||||||||||
|
|
0 |
1 |
R 2 |
sin x |
1 |
R Rx |
1 |
|
R R tg x, |
||||||||||||
|
|
|
|
|
|
|||||||||||||||||
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
||||
|
|
|
|
|
0 sin x x tg x , |
|
|
|||||||||||||||
|
|
|
|
|
0 |
cos x |
|
1 |
|
|
|
1 |
|
|
, |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
sin x |
x |
|
sin x |
|
|
|||||||||||
|
|
|
|
|
0 cos x |
sin x |
1 . |
|||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
||
|
Учитывая, что при x 0 |
|
lim cos x 1 0 , |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 0 |
|
|
|||||
lim 1 1 |
по принципу двустороннего ограничения получаем |
lim |
sin x |
1. |
||||||||||||||||||
|
||||||||||||||||||||||
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x 0 |
x |
|
|
|||||
Для x 0 |
вывод проводится аналогично. Получаем lim |
sin x |
1 . |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
x a |
x |
|
|
|
|
|
|
|
|
|
|||||||
Этот предел называется первым замечательным пределом. |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
§ МОНОТОННЫЕ ФУНКЦИИ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
10. Функция f (x) называется возрастающей на множестве X D(f ) |
если |
|||||||||||||||||||||
x1, x 2 X |
|
|
x1 x 2 f (x1 ) f (x |
2 |
) |
, или, что тоже самое |
||||||
x1, x 2 X |
|
|
f (x1 ) f (x 2 ) |
|
f (x 2 ) f (x1 ) |
0 . |
||||||
|
|
|
|
|
|
|||||||
|
|
|
x1 x 2 |
x 2 x1 |
|
|
|
|||||
20. Функция f (x) называется неубывающей на множестве X D(f ) если |
||||||||||||
x1, x 2 X |
|
|
x1 x 2 f (x1 ) f (x |
2 |
) |
, или, что тоже самое |
||||||
x1, x 2 X |
|
|
f (x1 ) f (x 2 ) |
|
f (x 2 ) f (x1 ) |
0 . |
||||||
|
|
|
|
|
|
|||||||
|
|
|
x1 x 2 |
x 2 x1 |
|
|
|
|||||
30. Функция f (x) называется убывающей на множестве X D(f ) если |
||||||||||||
x1, x 2 X |
|
|
x1 x 2 f (x1 ) f (x |
2 |
) |
, или, что тоже самое |
||||||
x1, x 2 X |
|
f (x1 ) f (x 2 ) |
|
|
f (x 2 ) f (x1 ) |
0 . |
||||||
|
|
|
|
|||||||||
|
|
|
x1 x 2 |
x 2 x1 |
|
|
|
|||||
40. Функция f (x) называется не возрастающей на множестве X D(f ) если
x1, x 2 X |
|
x1 x 2 f (x1 ) f (x |
2 |
) , или, что тоже самое |
|||
x1, x 2 X |
|
f (x1 ) f (x 2 ) |
|
f (x 2 ) f (x1 ) |
0 . |
||
|
|
|
|||||
|
|
x1 x 2 |
x 2 x1 |
||||
Из приведенных определений ясно, что понятие возрастания и убывания функции является понятием глобальным, в отличие от, скажем, непрерывности являющейся понятием локальным.
Функции возрастающие на множестве X или убывающие на множестве X называются монотонными функциями.
Для последовательностей:
10. Последовательность {xn} называется возрастающей, если
m,n N |
|
m > n xm > xn . |
20. Последовательность {xn} называется убывающей, если |
||
m,n N |
|
m > n xm < xn . |
30. Последовательность {xn} называется не возрастающей, если |
||
m,n N |
|
m > n xm xn . |
40. Последовательность {xn} называется не убывающей, если |
||
m,n N |
|
m > n xm xn . |
Для монотонных функций
*.Если функция монотонна на множестве, то она монотонна на всяком его подмножестве. *.Если функция одноименно монотонна на промежутках с общей точкой, то она одноименно монотонна на их объединении.
*.Максимальным промежутком монотонности называется такой промежуток монотонности, который не содержится ни в каком большем промежутке монотонности. *.Максимальные промежутки одноименной монотонности либо совпадают, либо не имеют общих точек.
*.Максимальные промежутки монотонности (разноименной) могут быть смежными и иметь общий конец.
§ АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ НАД МОНОТОННЫМИ ФУНКЦИЯМИ.
*. Сумма одноименно монотонных функций одноименно монотонна со слагаемыми.
*. Произведение положительных одноименно монотонных функций одноименно монотонно с сомножителями.
*. Изменение знака монотонной функции (умножение на ―-1‖ ) меняет тип монотонности на противоположный.
*. Изменение знака аргумента меняет тип монотонности на противоположный.
*.Переход от положительной монотонной функции f (x) к арифметически обратной ей
функции |
1 |
меняет тип монотонности на противоположный. |
|
|
|||
f (x ) |
|||
|
|
*. Взаимно-обратные функции одноименно монотонны.
*. Суперпозиция одноименно монотонных функций не убывает.
*. Суперпозиция разноименно монотонных функций не возрастает.
(При этом суперпозиция не строгая, если не строго монотонна хотя бы одна из функций).
Т. (о существовании предела монотонной ограниченной последовательности): Монотонная ограниченная последовательность имеет конечный предел. Монотонная последовательность всегда имеет предел (возможно не собственный).
∆ Пусть к примеру xn |
не возрастает и ограничена снизу . |
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
n |
xn xn 1 |
|
|
|
и |
|
|
|
inf xn = l* . |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Тогда |
> 0 |
N |
l* > xN > l*+ |
n > N |
|
|
|
|
l* < xn xN < l*+ |
|
▲. |
|
||||||||||||||||||||||||||||||
Пример: Рассмотрим последовательность |
x |
|
|
|
|
cn |
. |
|
|
|
|
|||||||||||||||||||||||||||||||
n |
n! |
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
1) |
c 0 . Тогда |
0 |
|
c |
1 |
начиная с некоторого номера . |
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
n 1 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
cn 1 |
|
c |
|
|
|
cn |
c |
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
||||||||||||||
x |
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
n |
, |
т.е. |
x |
|
и последовательность монотонно |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
n 1 ! |
|
n |
1 n! n |
1 |
|
|
|
|
|
|
n 1 |
|
|
|
|
|
n |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
убывает. При этом она ограничена снизу, т.к. |
x |
|
|
|
|
cn |
> 0 . |
|
|
|
|
|||||||||||||||||||||||||||||||
n |
n! |
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Следовательно |
|
|
|
|
|
lim xn b R . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
В равенстве: x n 1 |
|
|
c |
|
|
x n |
|
перейдем к пределу при n |
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
lim x n 1 lim |
|
c |
|
|
lim x n |
|
|
b = 0b = 0 |
|
|
|
|
|
b 0 |
lim x n |
0 . |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
1 |
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
n |
|
n n |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
n |
|
|
|
|
c |
n |
|
|
|
|
|
|
c |
|
n |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
lim |
|
|
lim |
|
|
|
|
lim |
|
|
|
|
|
|
0 , и отсюда lim x |
|
0 . |
||||||||||||||||||||||
2) c – любое: lim |
x |
n |
|
|
|
|
|
|
|
|
|
|
n |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
n! |
|
n! |
|
|
n! |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
n |
|
|
|
|
|
|
n |
|
n |
|
n |
|
|
|
n |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Т.к. величина является бесконечно малой тогда и только тогда, когда бесконечно малым является еѐ модуль.
§ ПЕРЕСТАНОВКИ, РАЗМЕЩЕНИЯ И СОЧЕТАНИЯ
Пусть имеется набор из n различных объектов.
Правило, по которому объектам A, B,C,... ставятся в соответствие элементы f (A), f (B),... из того же набора, причем каждый только один раз, называется
A |
B |
C |
D |
.... |
перестановкой из n элементов |
|
|
|
и количество |
|
f (B) |
f (C ) |
f (D) |
|
f (A) |
.... |
|||
перестановок обозначается Pn . |
|
|
|
|
Количество перестановок из n элементов |
Pn n (n 1) (n 2) .... 3 2 1 n! |
|||
Чтобы установить справедливость этой формулы представим себе, что необходимо заполнить n пронумерованных ящичков n различными шарами по одному в каждый ящичек. Тогда, первый ящичек можно заполнить любым из имеющихся n шаров, второй ящичек любым из оставшихся n–1 шаров, следующий любым из оставшихся n–2 шаров и т.д. Перемножая эти числа, мы и получим уже приведенную выше формулу.
Пусть требуется произвести выборку k элементов из набора в n различных элементов и, при этом считаются различными выборки не отличающиеся составом выбранных элементов, а отличающиеся только порядком, в котором выбираются эти k элементов. Такие выборки называются размещениями из n элементов по k и, количество
таких выборок обозначается Ak . |
Ak |
n! |
. |
|
|
|
|||
|
|
|||
n |
n |
(n k)! |
|
|
|
|
|
||
Установить справедливость этой формулы легко, если применить рассуждения аналогичные рассуждениям, приведенным при выводе формулы для перестановок из n элементов.
Выборки k элементов из набора в n элементов, когда различными считаются только выборки, имеющие разный состав, называются сочетаниями из n элементов по k .
Их количество обозначается C k , и при этом |
Ck |
Ank |
|
n! |
. |
|
|
|
|
||||
n |
n |
Pk |
|
k !(n k)! |
|
|
|
|
|
|
|||
Замечание при вычислении количества сочетаний мы иногда сталкиваемся с необходимостью вычислить 0! . Чтобы не записывать для этих случаев отдельные формулы, условились считать, что 0! 1. Оказалось, что такая договоренность не приводит к неприятностям, а позволяет вычислять Cnk и в тех случаях, когда в знаменателе стоит 0!.
Примеры:
1.Каково количество различных вариантов расположения команд в итоговой турнирной таблице футбольного чемпионата , если в нем принимают участие 16 команд Ответ Таких способов: P16 16! .
2.Каково количество различных вариантов распределения призовых мест (золото, серебро, бронза) Ответ При распределении призовых мест важным является не только то кто из участников стал призером, но и каким именно.
Поэтому, получаем :
A3 |
|
16! |
|
16 |
15 14 |
3360 . |
||
|
|
|
||||||
16 |
3 ! |
|||||||
16 |
|
|
|
|
||||
|
|
|
|
|
||||
3. Каково количество различных вариантов определения двух неудачников сезона, занявших два последних места (покидают высшую лигу) Ответ При определении неудачников важным является только то кто из участников занял последние два места и абсолютно неважно какое именно , ибо все равно обе команды покидают элитный дивизион.
Поэтому, получаем :
C 2 |
|
16! |
|
|
16 15 |
120 . |
|
|
|
||||
16 |
|
2!(16 2)! |
2 |
|
||
|
|
|
||||
§ БИНОМ НЬЮТОНА
Приведем и докажем очень важную формулу, предназначенную для возведения суммы двух слагаемых в натуральную степень. Эта формула называется формулой бинома Ньютона.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a b n (a b)(a b)...(a b) Cnk ak bn k . |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
∆ Доказательство теоремы проведем по методу математической индукции: |
|
|
||||||||||||||||||||||||||||||||||||||||||
а) При |
n 1 имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a b 1 C1k ak b1 k C10a0b1 C11a1b0 |
a b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
k 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
т. е. |
при n 1 равенство выполняется. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
б) Допустим равенство выполняется при n n |
|
т.е. |
a b n Cnk ak bn k . |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 0 |
|
|
|
|
|
|
|
|
||
Рассмотрим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
a b |
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
Cn a |
|
|
b |
|
|
|
|
|
|
|
|
|
b |
Cn a |
|
b |
|
|
= |
|||||||||||||||||||||
|
a b a b |
k |
n k |
a b Cn a |
k 1 |
n k |
k |
n k 1 |
||||||||||||||||||||||||||||||||||||
|
n 1 |
n |
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
k |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
k 0 |
|
|
|
|
|
|
|
|
|
|
|
k 0 |
|
|
|
|
|
|
|
|
k 0 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
=Cnn an 1bn n |
Cnk ak |
1bn k |
Cnk ak bn 1 k |
Cn0a0bn 0 1 = |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 0 |
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
a0bn 0 1 |
= |
|||||||||
|
|
|
=C n 1an 1bn 1 ( n 1) C k 1ak bn 1 k |
C k ak bn 1 k C |
0 |
|||||||||||||||||||||||||||||||||||||||
|
|
|
n 1 |
|
|
|
|
|
|
|
k 1 |
n |
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a0bn 1 0 |
|
|
||||
|
|
|
|
=C n 1an 1bn 1 ( n 1) (C k 1 C k )ak bn 1 k C 0 |
|
=… |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
n |
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
C k 1 C k |
|
|
|
|
|
|
|
|
|
n! |
|
|
|
|
|
|
|
n! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
n |
|
n |
|
|
(k 1)!(n k 1)! |
k!(n k )! |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
n! |
|
1 |
|
|
|
1 |
|
|
|
|
|
|
n! |
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
(k 1)!(n k )! n |
k 1 |
|
k |
|
|
|
(k 1)!(n k )! |
k (n k 1) |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
(n 1)! |
|
|
C k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
k!(n 1 k )! |
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
…=C n |
|
|
|
a0bn 1 |
n |
|
ak bn k |
C n 1an 1b0 |
n 1 |
|
|
ak bn k . |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
C k |
|
C k |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
k 0 |
n 1 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
т.е. из справедливости формулы при n n следует еѐ справедливость при n n 1 . По методу математической индукции формула бинома Ньютона доказана. ▲
Следствия из формулы бинома Ньютона:
|
n |
|
n |
|
|
|
|
|
Cnk |
(1 1)n 2n , |
( 1)k Cnk |
(1 |
1)n 0 . |
|
|
|
k 0 |
|
k 0 |
|
|
|
|
1 |
|
Свойство сочетаний: |
Ck 1 |
Ck Ck |
, |
||
|
|
|
|
n |
n |
n 1 |
|
1 1 |
|
полученное выше |
|
|
|
|
|
1 2 1 |
даѐт способ вычисления коэффициентов |
||||||
1 3 3 |
1 |
разложения (a b)n . Эти коэффициенты |
|||||
1 |
4 6 4 1 |
называются биноминальными. |
1 5 |
10 10 5 1 |
Этот способ демонстрирует, так называемый, |
… … … … ... |
треугольник Паскаля: |
|
§ ПРЕДЕЛ ФУНКЦИИ ПО ГЕЙНЕ ( ПО ПОСЛЕДОВАТЕЛЬНОСТИ)
Пределом функции f (x) по последовательности xn называется lim f (x n ) . |
|||
|
|
|
n |
Пример Рассмотрим |
f (x ) sin x . Для этой функции lim sin x не существует. |
||
|
|
|
x |
Однако при x n |
n |
f (x n ) sin n 0 |
и , следовательно, lim f (x n ) 0 . |
|
|
|
n |
Т . Если существует предел функции f (x) |
|
по всякой последовательности |
|
|
||||||||||||||||||||||||||||||||||||
xn a |
|
(xn D(f )) |
|
|
отличной от а то все эти пределы равны и существует |
|
||||||||||||||||||||||||||||||||||
равный их общему значению предел функции в точке а. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
∆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а) |
Пусть : |
xn a |
|
(xn a ) |
и |
|
|
|
|
|
a ) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
x n a |
( x n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
и пусть |
lim f (x |
n |
) b |
|
lim f (x ) b |
и |
b b . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
x такую, что: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Рассмотрим новую последовательность |
x |
x |
k |
а |
x |
x ( k N ) т.е. |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
2k 1 |
|
|
|
|
|
|
|
2k |
k |
|
|||||
между элементами последовательности x |
n |
вставим элементы последовательности x |
. |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
Учитывая, что x a , |
для этой последовательности получим |
lim f (x ) . |
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
Но … |
|
|
|
|
|
|
|
|
|
|
|
|
начиная с некоторого номера k1. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
f (x 2k 1 ) f (x k ) U b |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
f (x |
|
|
|
|
|
|
|
|
начиная с некоторого номера k2. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
2k ) f (x k ) U b |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
Тогда |
|
|
k k |
1 |
k k |
2 |
f (x ) U |
b |
f (x |
) U |
b |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Из свойства отделимости точек числовой прямой следует, что |
|
U b U b |
и значит |
|||||||||||||||||||||||||||||||||||||
не существует lim f (x |
) , если |
b b .Значит: |
b b . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) Пусть теперь lim f (x ) b . Здесь b общее значение пределов функции по всем |
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
x a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
последовательностям . Тогда: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
a D( f ) U b Va x D( f ) Va |
f (x ) U b . |
|
|
|
|
|
|||||||||||||||||||||||||
Построим последовательность |
x |
n |
такую, что: |
n N |
0 |
|
x |
n |
a |
|
|
1 |
. |
|
|
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Для нее |
f (x n ) U b |
и, |
следовательно, lim f (x n ) b , что вновь противоречит условию |
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
теоремы. Как говорится, противоречие доказывает теорему. ▲ |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
Доказанная теорема свидетельствует о том, что: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Предел функции по Гейне и по Коши – понятия эквивалентные. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
§ ЧИСЛО e. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
1 |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e lim |
1 |
|
|
|
|
2, 718281828459045... |
|
|
|
e -иррациональное число. |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
n |
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆ |
Рассмотрим последовательность xn : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
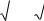
|
0 |
|
|
|
|
1 n |
|
|
|
|
|
|
1 |
|
|
|
n(n 1) |
|
|
1 |
|
|
|
|
n(n 1)(n 2) |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
1 |
|
. x |
n |
1 |
|
|
|
|
1 n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
.... |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n3 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
n |
|
|
|
|
|
|
n |
|
|
|
|
|
2! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
+…+ |
n(n 1)...(n k 1) |
|
1 |
|
|
... |
n(n 1)...(n n 1) |
|
|
1 |
= |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
nk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
nn |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
1 |
|
|
1 |
|
|
|
1 |
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
n 1 |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
1 1 |
|
1 |
|
|
|
|
... |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
... 1 |
|
|
|
|
|
|
... |
|
|
|
1 |
|
|
|
|
... 1 |
|
|
|
|
. |
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
n |
|
|
|
k ! |
|
|
n |
|
|
|
n |
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
n! |
|
|
|
|
n |
|
|
n |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
Тогда: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
x |
|
|
1 1 |
1 |
... |
|
1 |
... |
|
1 |
1 1 |
1 |
|
|
|
1 |
... |
1 |
|
|
|
3 . |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
k ! |
|
|
|
|
|
2n 1 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n! |
|
|
|
|
|
2 22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из последнего неравенства следует, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2,5 xn 3 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Т.е. последовательность xn -ограничена. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
1 |
|
n 1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
||||||||||||||||||
2 |
|
. x n 1 |
1 |
|
|
|
|
|
|
|
1 1 |
|
1 |
|
|
|
|
|
|
|
|
|
... |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
... 1 1 |
|
|
1 |
|
|
|
... xn |
, |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
k! |
|
n 1 |
|
|
|
|
|
|
|
|
|
|
n |
|
|
||||||||||||||||||||||||
|
т. е. |
x n 1 x n |
и, следовательно, последовательность |
|
xn |
|
возрастающая. |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
Таким образом, установлено, что последовательность |
|
xn монотонно |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
возрастающая и ограниченна сверху . Следовательно, существует и конечен предел этой |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
последовательности |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
lim 1 |
|
|
|
R. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Предел этой последовательности называется числом e . Некоторое количество первых значащих цифр его численного значения приведено выше.
Для их запоминания часто применяют следующее мнемоническое правило запомните число 2,7 далее два раза напишите год рождения Льва Толстого 1828 и два раза половина прямого угла 45, между которыми стоит прямой угол 90.
Обозначение e ввел Я. Эйлер ( e - первая буква в слове exponenta). Обозначение стало общеупотребительным, так как напоминает и об Я. Эйлере ( e - первая буква фамилии
Euler Leonard, 1707-1783).
|
|
|
|
1 n |
|||
|
e lim 1 |
|
. |
||||
|
|
||||||
|
|
|
|
n |
|||
Эйлер ввел также (греч. |
- окружность) в 1736 г. И хотя еще в 1706 г. то |
||||||
же сделал У. Джонсон (W. Johnson), только после Эйлера обозначение стало обще |
|||||||
употреби-тельным. |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
2 |
|
|
|
|
|
|
3 , 3.141…3.146 |
||||||
Тот же результат можно получить, воспользовавшись неравенством Я. Бернулли:
1 x 1 x |
если x 1 и 0 , причем " " x 0 n 1. |
|
|||
Для натурального n , |
n N , и положительного |
x 0 неравенство |
очевидно из |
||
формулы бинома: |
|
|
|
|
|
1 x n 1 1 nx |
n n 1 |
x2 ... 1 nx . Для натурального n , n N , |
и 1 x 0 |
||
|
|||||
2 |
|
|
|
|
|
доказывается методом математической индукции: первый шаг индукции 1 x 1 1 1 x ,

предположение индукции 1 x n 1 nx , индуктивный шаг
1 x n 1 1 x n 1 x 1 nx 1 x 1 n 1 x nx2 1 n 1 x .
В общем случае (для вещественных показателей) легко доказывается методами дифференциального исчисления.
Для последующего рассуждения требуется только доказанное здесь ( n натуральное).
xn 1
xn
|
|
1 |
|
n 1 |
||
|
1 |
|
|
|
|
|
|
|
|
|
|||
|
|
n 1 |
||||
|
|
1 |
n |
|||
|
||||||
|
1 |
|
|
|||
|
n |
|||||
|
|
|
|
|||
|
|
1 n n 2 n |
|
|
1 |
|
1 |
|
n |
|||||
1 |
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
> |
|
n 1 |
2 |
|
n 1 |
2 |
|||||||||
|
|
n 1 |
|
|
|
|
n 1 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
n 1 1 |
|
|
n 1 1 |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n |
1 |
2 |
|
n |
|
|
n 1 |
2 |
|
n 1 |
3 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
= |
|
|
1 |
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1. |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
n 1 |
n 1 |
n 1 2 |
|
n 1 2 |
n 1 3 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
- последовательность xn |
возрастает ( xn 0 ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
Далее определим последовательность: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
1 |
1 |
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
zn |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
n 1 |
2 |
n 1 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
z |
|
x . |
|
|
Тогда для нее: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
= |
|
|
= |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
n |
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
n |
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 2 |
|
|
|
n 2 n n 2 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
n 1 |
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
= |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
> |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n n 2 |
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
n n 2 |
|
|
|
|
|
|
|
|
n 2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
> |
|
1 |
|
|
1 |
|
|
|
|
n 1 |
|
|
|
|
n 1 1 1 |
|
= 1 |
|
|
|
1 |
|
|
|
|
|
> 1. |
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
n 2 |
|
n n 2 |
|
n n 2 2 |
|
|
n n 2 2 |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
- последовательность zn убывает. Очевидно n |
xn |
|
zn . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Если n n , n , |
то |
|
n, n |
|
|
|
x1 xn |
zn |
|
z1 - любой член одной последовательности |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ограничивает другую последовательность. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
Следовательно: lim xn lim zn . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
Но zn |
|
xn |
1 |
|
|
|
|
lim xn lim zn . |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
§. РЯД ДЛЯ e. SERIES FOR e. |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
Отбрасывая в выражении для xn |
|
все (положительные) слагаемые после k+1 имеем: |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
x |
|
1 1 |
|
1 |
1 |
1 |
... |
1 |
1 |
1 |
... 1 |
k 1 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2! |
|
|
n |
|
|
|
|
|
|
k! |
|
|
|
n |
|
|
|
|
|
n |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
Существование предела слева доказано, предел справа очевидно существует, поэтому в пределе n получаем двойное неравенство:
e 1 1 |
1 |
|
... |
1 |
y |
|
x |
|
; |
k . |
|
|
k |
k |
|||||||
2! |
|
k! |
|
|
|
|||||
|
|
|
|
|
|
|||||
