Неопределенный интеграл
1.
Задачи для решения. Демидович. 1628, 1635,
1636, 1640,1643, 1646,1648, 1649, 1656, 1658,
1659, 1662, 1663, 1665,1677, 1681, 1682, 1685.
Вычислить неопределенные интегралы:
1628.
.1635.
.
1636.
.
1640.
.
1643.
.
1646.
.
1648.
.
1649.
.
1656.
.
1658.
.
1659.
.
1662.
.
1663.
.
1665.
.
.
1677.
.
1681.
.
1682.
.
1685.
.
2.
Задачи для решения. Демидович. 1709, 1715*,
1723, 1727, 1729, 1733, 1737, 1747, 1749, 1768,
1774, 1777, 1792, 1799, 1808, 1811, 1819.
1709.
.1715*.
.
1723.
.
33
1727.
.1729.
.1733.
.
1737.
.1747.
.1749.
.1768.
.1774.
.1777.
.
1792.
.1799.
.
1808.
.1811.
.1819.
.
3.
Задачи для решения. Демидович. 1837, 1843, 1851, 1853, 1857,
1859, 1864, 1866, 1867, 1869, *, 1872, 1878, 1882, 1892, 1893.
1837.
.
1843.
.
1851.
.
1853.
.
1857.
.
1859.
.
1864.
.
1866.
.
1867.
.
1869.
.
*.
.
1872.
.
1878.
.
1882.
.
1892.
.
1893.
.
34
4.
Задачи для решения. Демидович. 1896, 1904,
1914, 1920, 1928,1933*, 1938, 1948, 1952, 1954,
1968, 1971, 1977, 1981, 1987, 1995.
1896.
.1904.
.
1914.
.1920.
.
1928.
.1933*.
.
1938.
.1948.
.
1952.
.1954.
.
1968.
.1971.
.
1977.
.1981.
.
1987.
.1995.
.
4.
Задачи для решения. Демидович. 2012, 2072, 2076, 2080,
2084, 2098, 2022, 2035, 2167, 2168, 2171, 2172, 2173, 2176.
2012.
Вывести
формулы понижения для интегралов
и
и с их помощью
вычислить интегралы:
;
.
35
2072.
.
2076.
.2080.
.2084.
.2098.
.
2022.
.2035.
.2167.
.2168.
2171.
.
2173.
.
2166.
.2169.
.
2174.
,где
.
*** Дополнение 1.
Подстановки Эйлера:
:
;
2)
;
3)
(D
> 0) .
Подстановки Чебышева (Дифференциальный бином):
:
1) рZ; x = tN (N – общий знаменатель m и n);
2)
;
(a
+ bxn)
= tN
(N
– знаменатель p);
3)
;ax–4
+ b
= tN
(N
– знаменатель p).
Тригонометрические подстановки:
1) R(–sinx, cosx) = –R(sinx, cosx): cosx = t;
2) R(sinx, –cosx) = –R(sinx, cosx): sinx = t;
3) R(–sinx, –cosx) = R(sinx, cosx): tgx = t;
36
4) Универсальная тригонометрическая подстановка:
.
Универсальная гиперболическая подстановка:
.
*** Дополнение 2.
Некоторые формулы полезные при интегрировании:
;
;
;
;
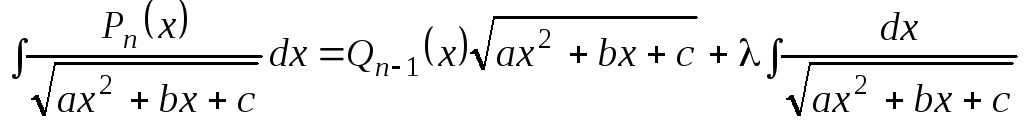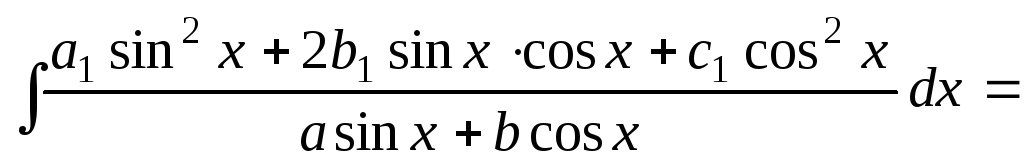
5.
,
где
1,
2
– корни уравнения
,
ui
= (a
– i)sinx
+bcosx,
;
6.
;
7.
.
( | a | | b | ).
37
Экзаменационные задачи по курсу
“математическИЙ анализ”.
I курс (первый семестр).
Э1.
1. Запишите в символах утверждение о том, что последовательность {xn} не является возрастающей, как отрицание того, что последовательность {xn} растет, и в положительном смысле как формулу с тесными отрицаниями, в которой отрицания не относятся к подформулам, составленным с помощью логических связок.
2. Укажите биекцию промежутка [0, 1] на промежуток [-1, 2] и на R+.
3. Докажите, что множество действительных чисел – несчетно.
4. Докажите счетность множества рациональных чисел.
5. Найдите соотношение между нижними и верхними гранями множества и его над(под) множества.
6. Найдите sup(A U B) и inf(A U B).
7. Дайте определение квантора существования и единственности () и выясните его поведение относительно отрицания.
Найти следующие пределы:
8.
.
9.
.
10.
.
11.
.
12.
.
13.
.
14.
.
15.
..
38
Э2.
1.
.
2.
.
3.
.
4.
.
5.
.
Найтиa
и b.
6.
.
7.
.
8.
;
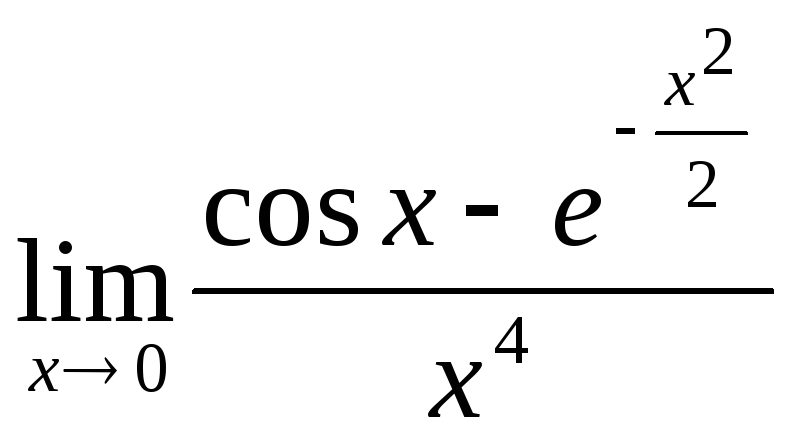9. Определить главный член функции y(x) = tg(sinx) – sin(tgx) при x 0.
10. При х 0 определить главный член простейшего вида для функции: у = (1 + х)х – 1.
В следующих задачах найти наибольшее п и константы А, В, С,… такие, чтобы при х → 0 были справедливы формулы:
11.
.
12.
.
13.
.
14.
.15.
.
Э3.
1. Определить какого порядка производными обладает в точке
х
= 0 функция
и вычислить в этой точке все соответствующие
производные.
39
2. Исследовать на непрерывность функцию
.
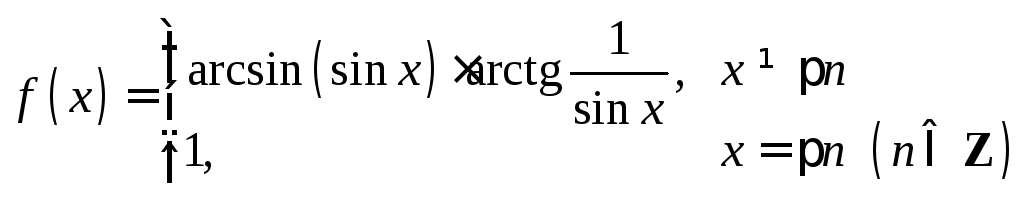3.
Исследовать на непрерывность функцию
и построить эскиз ее графика.
4.
Найти наибольший член последовательности
.
5. Изобразите на плоскости (p, q) области, в которых уравнение х3 + рх + q = 0 имеет:
а) один и б) три вещественных корня.
6. Из какого сектора круга радиуса R можно свернуть воронку наибольшей вместимости?
7. Определите число вещественных корней и отделите их для уравнения: 3х4 – 4х3 – 6х2 + 12х – 20 = 0.
8. Найдите расстояние от начала координат до касательной к кривой x = a(cost + tsint), y = a(sint – tcost).
9. В шар радиуса R впишите цилиндр наибольшего объема.
10. Исследовать на экстремум функцию: f(x) = cos100x + ch100x.
11. Определить промежутки монотонности функции:
y = x + | sin2x |.
12. Определить количество вещественных корней уравнения:
x3 + 3x2 + 2x – 12 = 0 и указать промежутки, на которых они находятся.
13.
Найти sup и inf функции
дляx(0,
+ ).
14. Найти количество вещественных корней уравнения:
x3 – х + а = 0 при различных значениях параметра а.
15.
Найти:
y(n),
если
.
40
Э4.
Найти:
1.
,
если
,y
= tgt
– t.
2. y(n),
если y
= e2xsin2x.
3.
.
4.
.
5. y(n), если y = cos3x. 6. y(n), если (2x – 1)23x32x.
7.
.
8.y(n),
если y
= sin2axcos2bx.
9.
,
еслиy
= sinxsin2xsin3x.
10.
.
11.
,
еслиy
= xsinxcos2x.
12. (sin4x + cos4x)(n). 13. y(101)(1), если y = (x2 – x)cos3x.
14.
,
если x2
+ 2xy
– y2
= 2x.
15. y(20), если y = x2e2x.
Э5.
1.
.
2.
,
если y
= (tg2x)sinx.
3.
.
4.
Для функции
найдите
и
дляxR.
5. Показать, что уравнение ctgx = kx xR имеет в интервале x(0, ) единственный непрерывный корень x = x(k).
Докажите неравенства и равенства:
6.
.
41
7.
.
8.
.
9.
.
10.
.
11.
.
12.
Покажите, что у многочлена Лежандра
все корни вещественны и заключены в
интервале (–1, 1).
13. Доказать, что если все корни многочлена Pn(x) с вещественными коэффициентами вещественны, то и Pn(x) имеет только вещественные корни.
Построить графики функций:
14.
.
15.
.
Э6.
Найти разложение указанной функции по формуле Тейлора в окрестности указанной точки до указанной степени включительно:
1.
,x0
= 0 до х4.
2. y
= arctgx,
x0
= 0 (весь ряд).
3. y = ln(1 + x + x2 + x3), x0 = 0 до x5.
4.
,x0
= 0 до x2n+1.
42
5. y = tgx, x0 = 0 до x5 6. y = (x2 – 1)1990, х0 =1 до (х – 1)1990.
7.
,х0
= 0 Получить два члена разложения.
8. При х найти три члена асимптотики функции
.
9. Напишите полином Тейлора функции ех в нуле, который, позволил бы вычислить значение ех на отрезке [–1, 2] с точностью до 10–3.
Оцените абсолютные погрешности формул:
10.
;
|x
|
1.
11.
;
|x
| > 102.
12.
;
|x
| > 103.
Вычислить указанные значения с заданной точностью:
13.
;
= 10–6.
14.
;
= 10–6
15.
е;
= 10–6.
.
Э7.
1. ln2 ; = 10–6. 2. arcsin0,56; = 10–5.
3.
;
= 10–4
4.
;
= 10–5.
5. Найдите сумму: 1 + 2x + 3x2 + 4x3 + … + nxn–1.
6. Найти остаток от деления многочлена z1989 – 1 на z2 + 1.
7.
Решить систему уравнений:
.
8. Определите, при каких действительных значениях x и y сопряжены следующие комплексные числа: z1 = y2 – 7y – 9xi и z2 = – 12 + 20i + x2i.
9. Найдите формулу для суммы: sinx + 2sin2x + … + nsinnx.
10. Выразить sin5 через тригонометрические функции кратных углов, а sin5 через степени sin и cos .
43
11. Найти множество точек комплексной плоскости, заданное условием:
| z – 2 |2 + | z + 2 |2 = 26.
12. Найти все значения: а) 1; б) ii.
13.
Найти множество точек комплексной
плоскости, заданное условием:
14. Решите систему уравнений: | z + 1 – i | = | 3 + 2i – z | = | z + i |.
15.
Решить уравнение:
Э8.
1.
Найти все значения:
.
2. Разложить на неприводимые множители с вещественными коэффициентами, многочлен z2n + 1 – 1.
3. Решите уравнение: z6 – z3 – 2 = 0.
4. Разложить x2n + 1 на неприводимые множители с вещественными коэффициентами.
5. Уравнение 3x4 – 5x3 + 3x2 + 4x – 2 = 0 имеет корень 1 + i. Найдите остальные корни.
6. Разложить x2n – 1 на неприводимые множители с вещественными коэффициентами.
7. Какую кривую в комплексной плоскости описывает точка: z = at + beit, если tR, a, b, – вещественны.
8. Решить уравнение: z10 – z5 – 992 = 0.
9. Решить уравнение: (z – i)z(z + i)(z + 2i) = 24.
10. Решить уравнение: z5 + z4 + z3 + z2 + z + 1 = 0.
11. Решить уравнение: z4 – 30z2 + 289 = 0.
12. Найти множество точек, удовлетворяющих условиям:
.
13. Нарисуйте множество точек, удовлетворяющих условию:
.
44
14. Какую кривую в плоскости z описывает точка
z = (a + it)eit, tR (а – вещественно).
15. Нарисуйте множество точек, удовлетворяющих условию:
| Re{z(cos2 + isin2)}| + | Im{z(cos2 + isin2)}| 1.
Э9.
Вычислить неопределенные интегралы:
1.
.
2.
.
3.
,
4.
.
5.
.
6.
.
7.
,
.
8.
.
9.
.
10.
.
11.
.
12.
.
13.
.
14.
.
15.
.
Э10.
1.
.
2.
.
45
3.
.
4.
.
5.
,
6.
.
7.
,
.
8.
.
9.
.
10.
.
11.
.
12.
.
13.
.
14.
.
15.
.
Э11.
1.
.
2.
. 3.
.
4.
.
5.
.
6.
.
7.
.
8.
.
9.
.
10.
.
11.
.
46
12. Выразите через интегральный логарифм Li(x) и элементарные функции, интегралы:
а)
;
б)
.
13. Выразите через интегральный синус Si(x) и элементарные функции, интегралы:
а)
; б)
.
14. Выразите через интеграл ошибок erf(x) и элементарные функции, интегралы:
а)
, б)
.
15. Исключите интегрирование неэлементарных функций:
а)
;
б)
; в)
.