
- •Ориентировочный план занятий
- •Элементы элементарной математики
- •Формулы сокращенного умножения. Метод интервалов решения дробно-рациональных (и не только!) неравенств.
- •Системы двух и трех линейных уравнений. Совместимость, определенность, неопределенность. Метод Гаусса исключения неизвестных.
- •Многочлены. Теорема Безу и ее следствия. Рациональные корни уравнений. Схема Горнера. Возвратные уравнения.
- •Степенная, показательная, логарифмическая функции. Основные свойства и графики. Решение показательных и логарифмических уравнений и неравенств.
- •Тригонометрические функции углового и числового аргументов. Определение и свойства. Обратные тригонометрические функции. Формулы двойного и половинного аргумента. Формулы приведения.
- •Решение простейших (и не только!) тригонометрических уравнений и неравенств.
- •Построение графиков функций с помощью элементарных движений. Общая схема исследование функций с помощью производной.
- •Метод сечений при решении задач с параметром. Задачи, связанные с исследованием функций.
- •Элементы математической логики и теории множеств
- •I. Математическая логика
- •План занятий
- •Задачи для решения 1*, 2*, …, 7*
- •II. Элементы теории множеств
- •Задачи для решения 1*, 2*, 3*, 4*
- •Теория пределов
- •Задачи для решения. Демидович 656, 657,658, *, *, *.
- •*** Дополнение. Формулы, связанные с замечательными пределами
- •І. Замечательные пределы:
- •Непрерывность и дифференцируемость
- •Применения дифференциального исчисления
- •Комплексные числа
- •Задачи для решения. Волковысский 1*, 1, 2*, 2, 3*, 3, 7, 8, 4*.
- •Неопределенный интеграл
- •Экзаменационные задачи по курсу
- •I курс (первый семестр).
- •Экзаменационные вопросы по курсу
- •Первый курс. Первый семестр
- •Контрольная работа № 1.
- •Контрольная работа № 5. Свойства функции на языке -.
- •Контрольная работа № 6.
- •Контрольная работа № 14.
- •Контрольная работа № 19.
Контрольная работа № 1.
Функции и их графики.
Зная
график функции
![]() ,
построить графики следующих функций
,
построить графики следующих функций

![]()
2.
![]()
3.![]()
4.
![]()
5.![]()
6.
![]()
7.
7.![]()
8.
![]()
9.
9.![]()
10.
![]()
11.
11.![]()
12.
![]()
13.
13.
![]()
Контрольная работа № 2.
Элементы математической логики.
Установить, какие значения истинности принимают следующие составные высказывания при различных значениях входящих в них пропозициональных переменных
1.
![]() .
.
2.
![]() .
.
3.
![]() .
.
4.
![]() .
.
5.
![]()
6.
![]() .
.
7.
![]() .
.
8.
![]() .
.
9.
![]() .
.
10.
![]() .
.
53
11.
![]() .
.
12.
![]() .
.
13.
![]() .
.
14.
![]() .
.
Контрольная работа № 3.
Элементы теории множеств.
Доказать, что
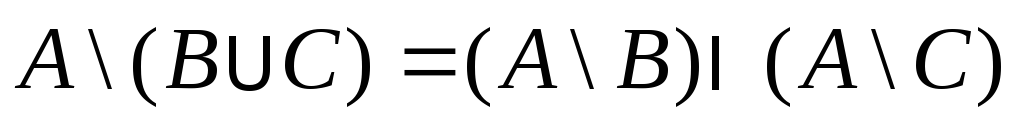 .
. .
.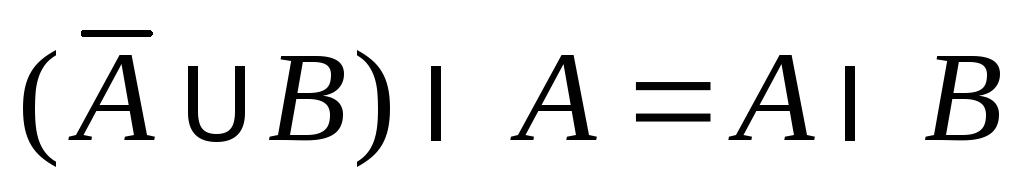 .
. .
. .
. .
. .
.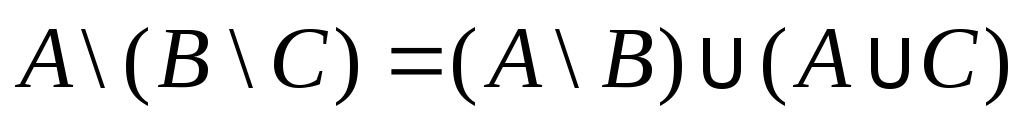 .
. .
. .
.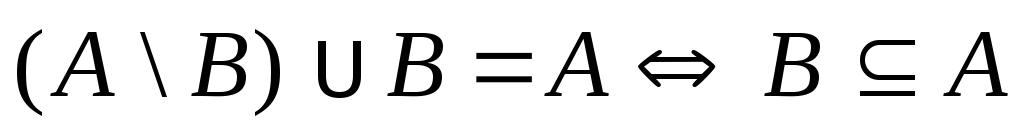 ,.
,. .
.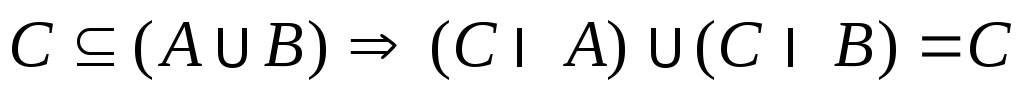 .
.
Контрольная работа № 4.
Верхние и нижние границы функции.
Доказать следующие утверждения
Используя язык доказать, что функция
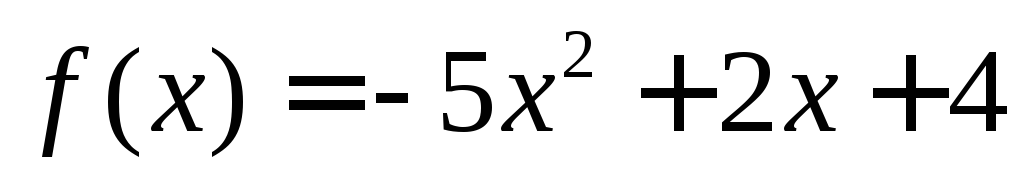 не имеет нижней границы.
не имеет нижней границы.Используя язык доказать, что функция
 не имеет верхней границы.
не имеет верхней границы.Используя язык доказать, что функция
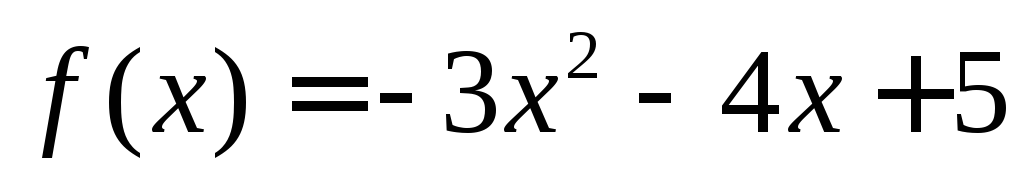 не имеет нижней границы.
не имеет нижней границы.
54
Используя язык доказать, что функция
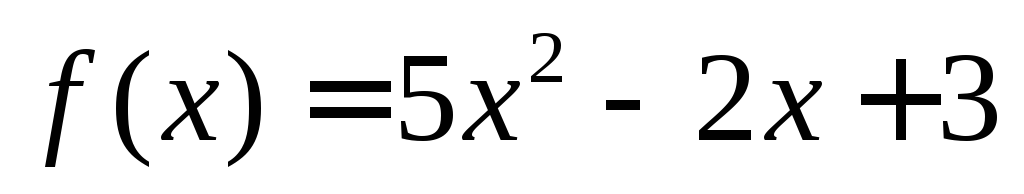 не имеет верхней границы.
не имеет верхней границы.Используя язык доказать, что функция
 не имеет нижней границы.
не имеет нижней границы.Используя язык доказать, что функция
 не имеет верхней границы.
не имеет верхней границы.Используя язык доказать, что функция
 не имеет нижней границы.
не имеет нижней границы.Используя язык доказать, что функция
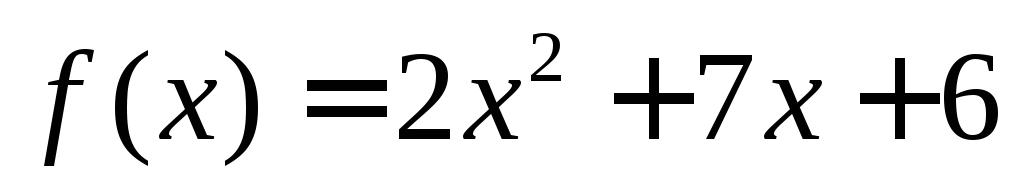 не имеет верхней границы.
не имеет верхней границы.Используя язык доказать, что функция
 не имеет нижней границы.
не имеет нижней границы.Используя язык доказать, что функция
 не имеет верхней границы.
не имеет верхней границы.Используя язык доказать, что функция
 не имеет нижней границы.
не имеет нижней границы.Используя язык доказать, что функция
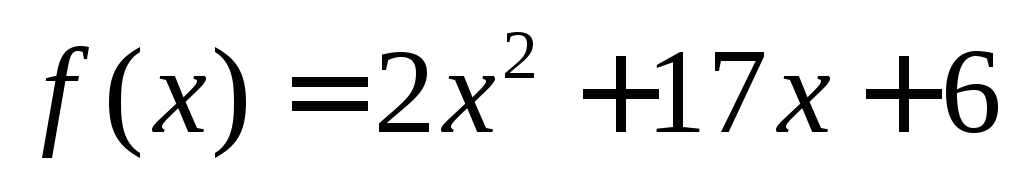 не имеет верхней границы.
не имеет верхней границы.Используя язык доказать, что функция
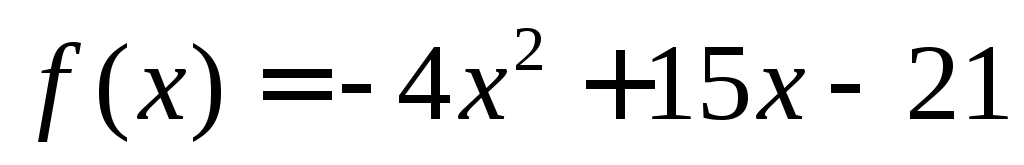 не имеет нижней границы.
не имеет нижней границы.
Контрольная работа № 5. Свойства функции на языке -.
В положительном смысле на языке сформулировать следующие утверждения
1.
Функция
![]() не имеет конечного предела при
не имеет конечного предела при![]() .
.
2.
Функция
![]() – бесконечно малая величина при
– бесконечно малая величина при![]() .
.
3.
Функция
![]() имеет конечный предел при
имеет конечный предел при![]() .
.
4.
Функция
![]() не имеет конечного предела при
не имеет конечного предела при![]() .
.
5.
Функция
![]() – бесконечно малая величина при
– бесконечно малая величина при![]() .
.
6.
Функция
![]() – не бесконечно малая величина при
– не бесконечно малая величина при![]() .
.
55
7.
Функция
![]() – бесконечно большая величина при
– бесконечно большая величина при![]() .
.
8.
Функция
![]() –
не бесконечно большая величина при
–
не бесконечно большая величина при![]() .
.
9.
Функция
![]() – величина отделенная от нуля при
– величина отделенная от нуля при![]() .
.
10.
Функция
![]() – не величина отделенная от нуля при
– не величина отделенная от нуля при![]() .
.
11.
Функция
![]() – величина ограниченная при
– величина ограниченная при![]() .
.
12.
Функция
![]() – величина неограниченная при
– величина неограниченная при![]() .
.
13.
Функция
![]() имеет конечный предел при
имеет конечный предел при![]() .
.
Контрольная работа № 6.
Предел функции на языке -.
В каждом варианте два задания
1). Утверждение на языке записать на языке .
2). Утверждение на языке записать на языке .
1).
 при
при
2).
![]() .
.
1).
 при
при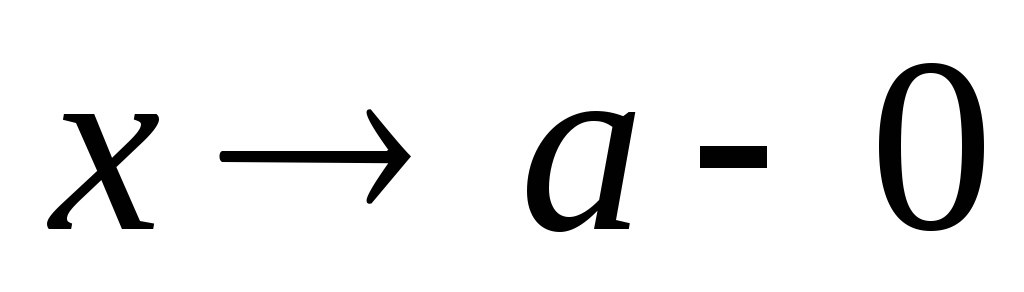
2).
![]() .
.
1).
 при
при
2).
![]() .
.
1).
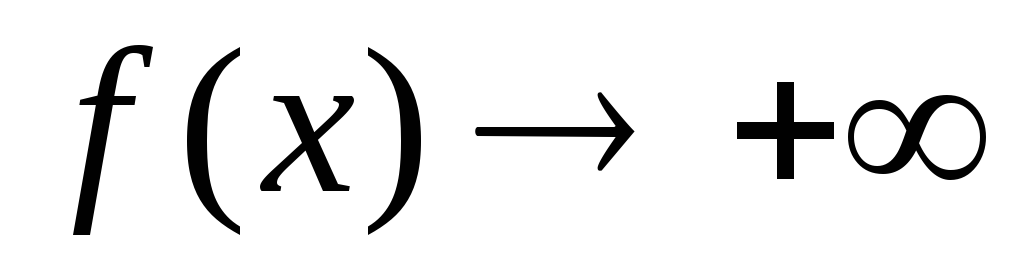 при
при
2).
![]() .
.
1).
 при
при
2).
![]() .
.
1).
 при
при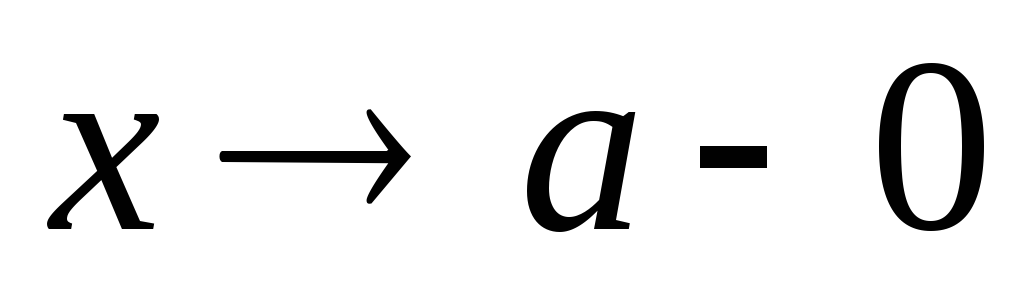
2).
![]() .
.
1).
 при
при
2).
![]() .
.
1).
 при
при
2).
![]() .
.
1).
 при
при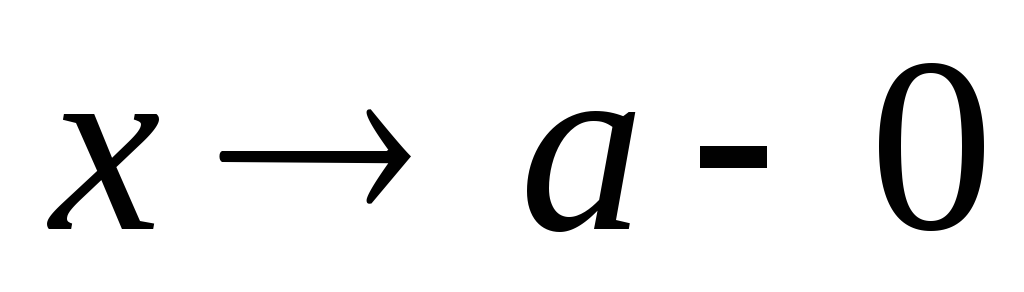
56
2).
![]() .
.
1).
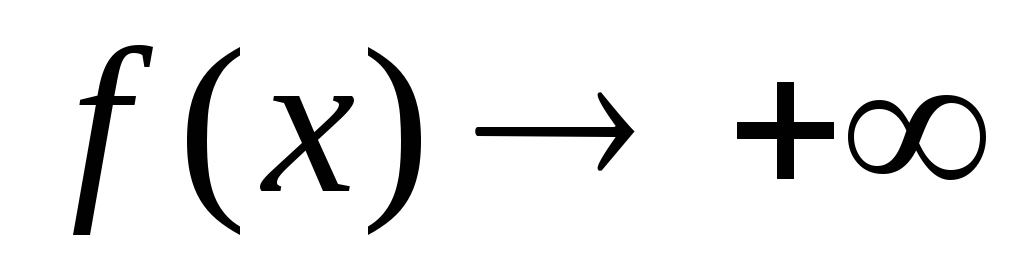 при
при
2).
![]() .
.
1).
 при
при
2).
![]() .
.
1).
 при
при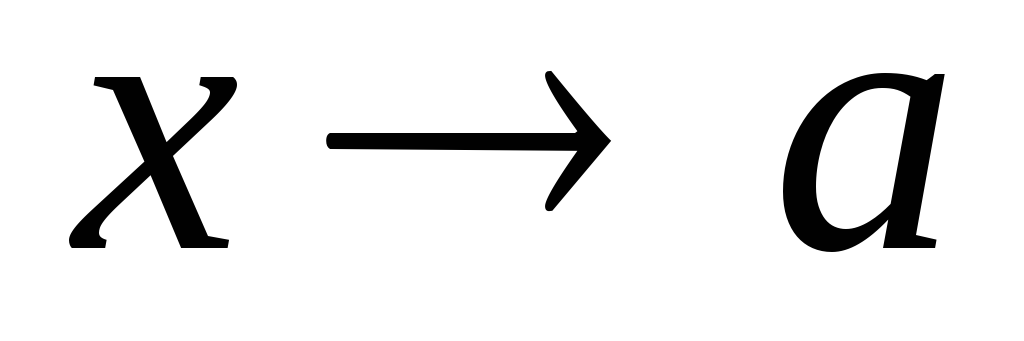
2).
![]() .
.
1).
 при
при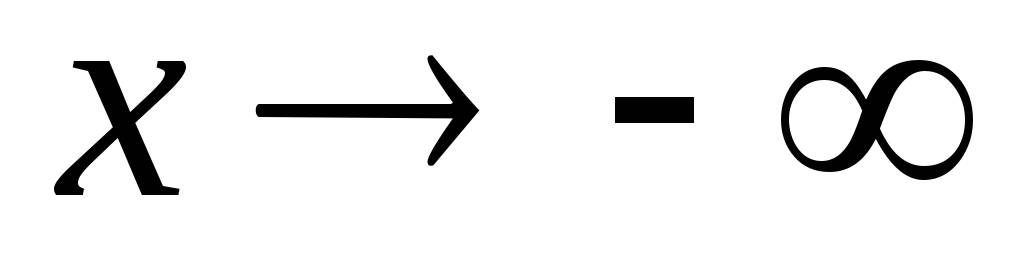
2).
![]() .
.
Контрольная работа № 7.
Предел функции .
Найти следующие пределы
1.
![]() .
2.
.
2.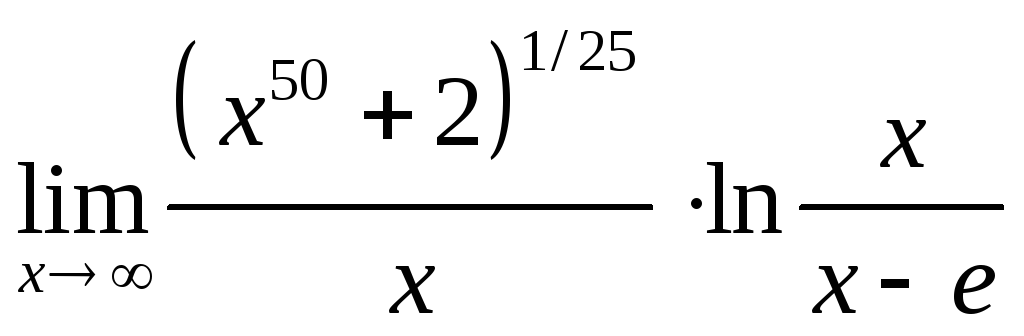 .
.
3.
 .
4.
.
4.![]() .
.
5.![]() 6.
6.![]()
7.
 .
8.
.
8.![]() .
.
9.
![]() .
10.
.
10.![]() .
.
11.
 .
12.
.
12.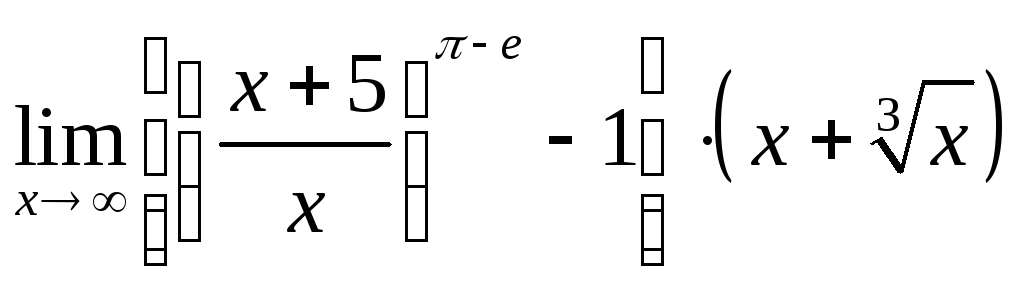 .
.
13.
![]() .
.
57
Контрольная работа № 8.
Использование основных эквивалентностей .
В указанных предельных процессах найти главные члены простейшего вида для следующих величин
1.
![]() при
при![]() .
.
2.
![]() при
при![]() .
.
3.
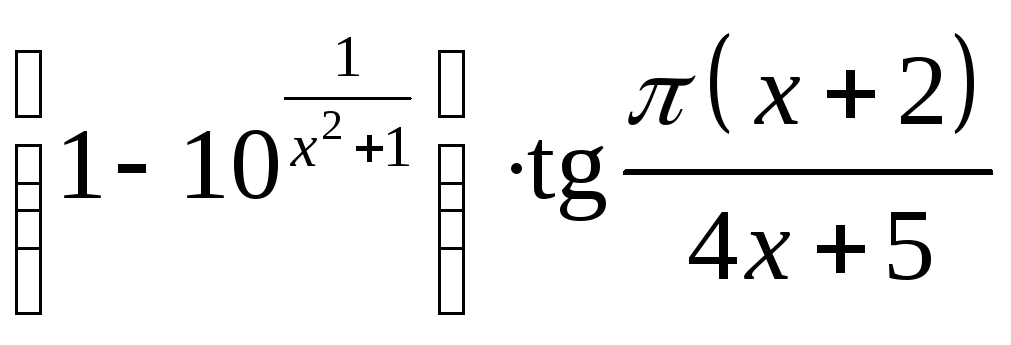 при
при![]() .
.
4.
 при
при![]() .
.
5.
![]() при
при![]() .
.
6. при
при![]() .
.
7.
![]() при
при![]() .
.
8.
![]() при
при![]() .
.
9.
![]() при
при![]() .
.
10.
![]() при
при![]() .
.
11.
![]() при
при![]() .
.
12.
![]() при
при![]() .
.
13.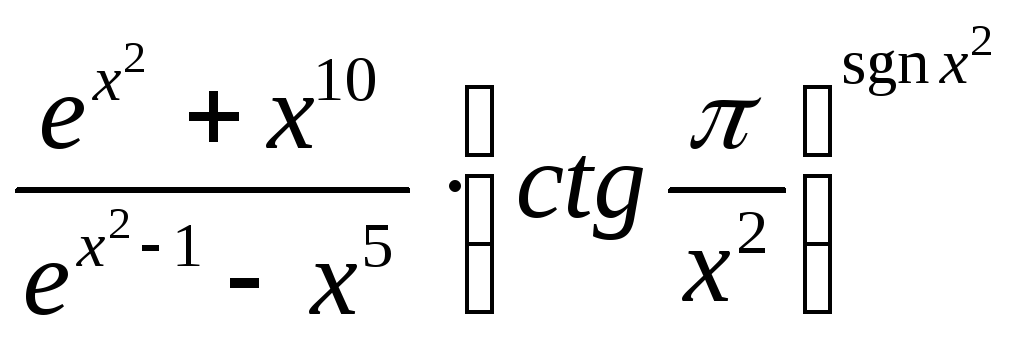 при
при![]() .
.
58
Контрольная работа № 9.
Исследование функций на непрерывность.
Исследовать следующие функции на непрерывность:
1.
![]() ;
2.
;
2. ;
;
3.
 ;
4.
;
4. ;
;
5.
![]() ;
6.
;
6. ;
;
7.
 ;
8.
;
8.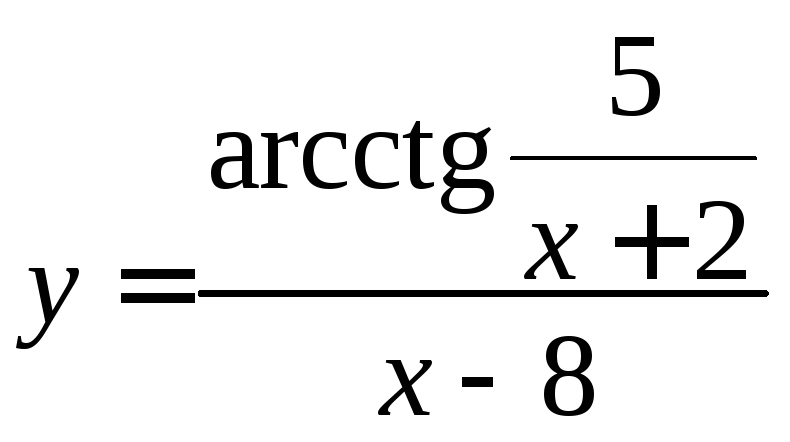 ;
;
9.
![]() ;
10.
;
10.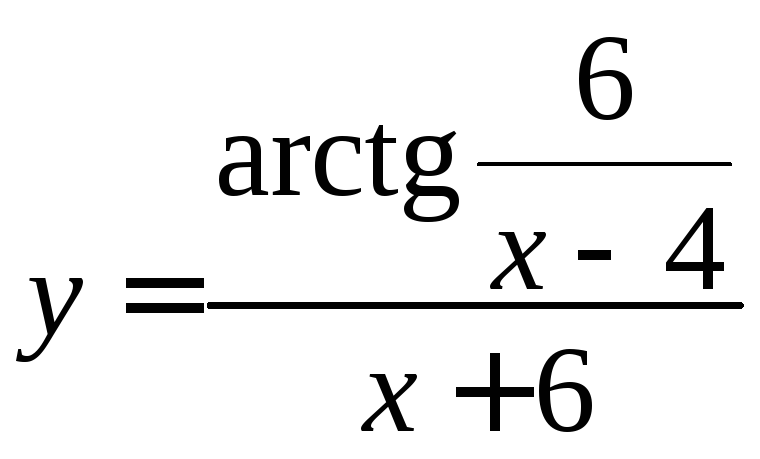 ;
;
11.
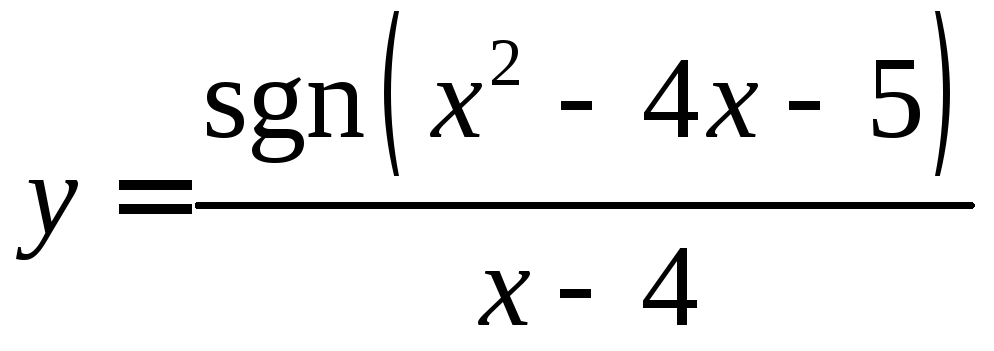 ;
12.
;
12. ;
;
13.
![]() .
.
Контрольная работа № 10.
Классификация точек разрыва.
Найти точки разрыва следующих функций и указать их характер
 .
2.
.
2.
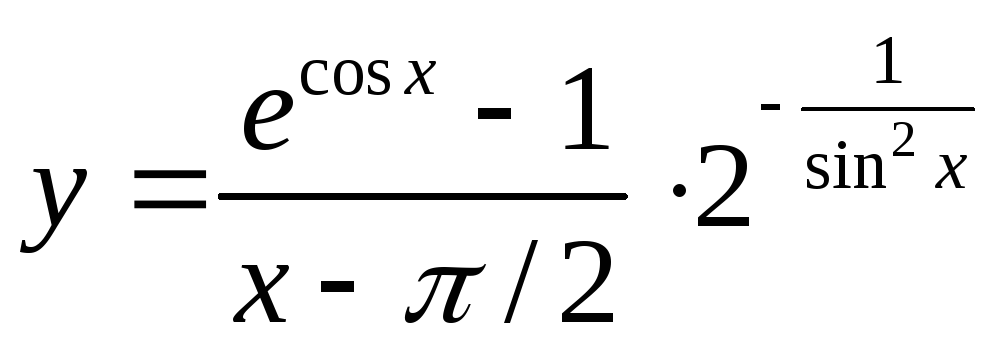 .
.
3.
![]() . 4.
. 4.![]() .
.
59
5.
![]() .
6.
.
6.
![]() .
.
7.
![]() .
8.
.
8.![]() .
.
9.
![]() .
10.
.
10.
![]() .
.
11.
![]() .
12.
.
12.![]() .
.
13.
![]() .
.
Контрольная работа № 11.
Производная функции 1.
Найти производные следующих функций
1.
![]()
2.
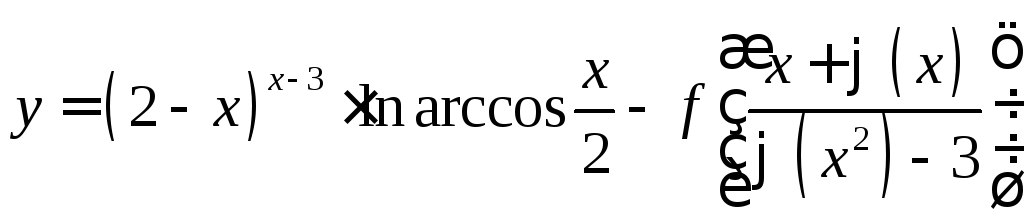
3.
![]()
4.
![]()
5.
![]()
6.
![]()
7.

8.
![]()
9.
![]()
60
10.
![]()
11.
![]()
12.
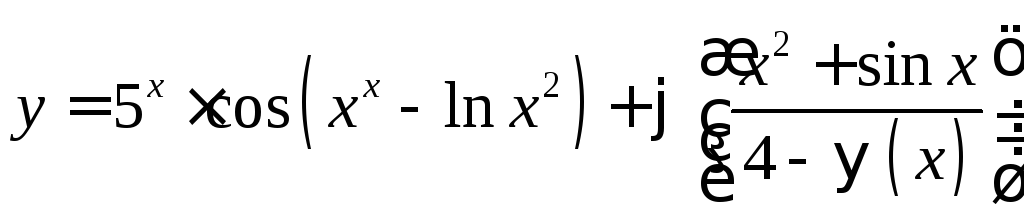
13.
![]() .
.
Контрольная работа № 12.
Производная функции 2.
Найти указанные производные от заданных функций. При дифференцируемости по одной из переменных, остальные считать фиксированными.
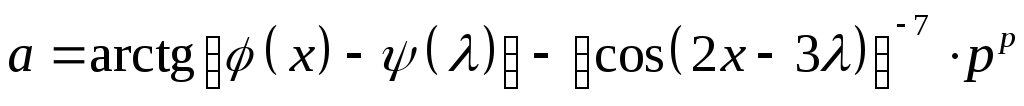
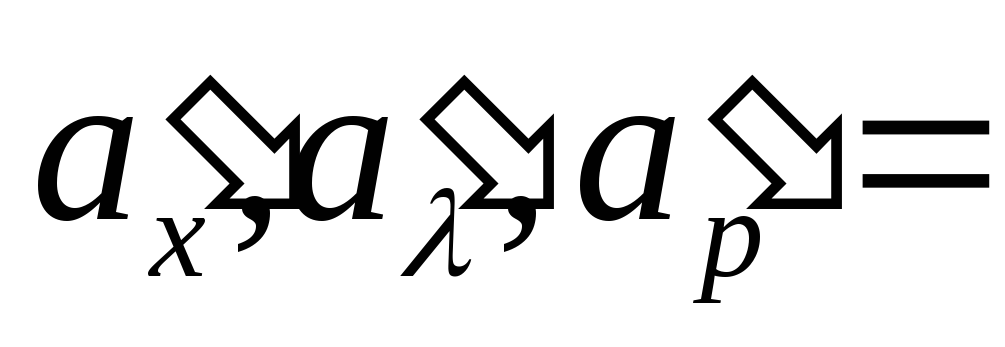
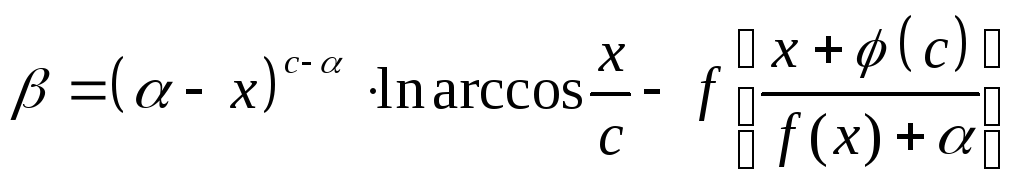
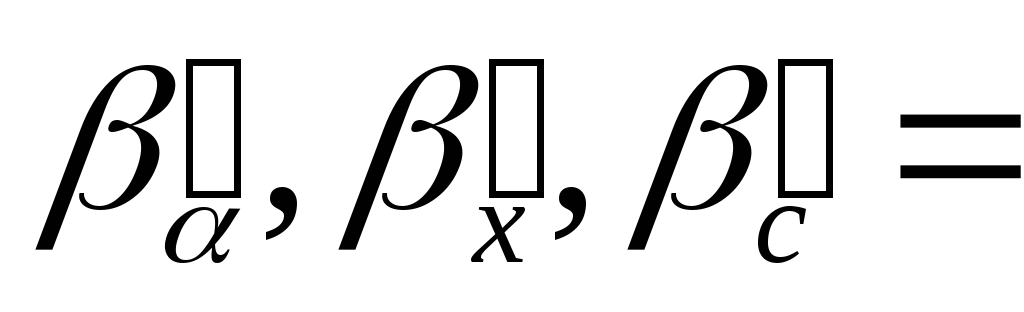
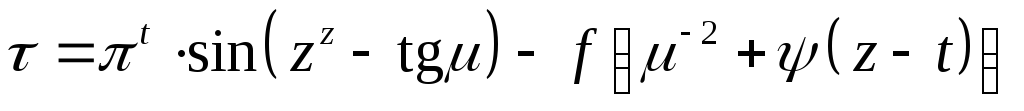

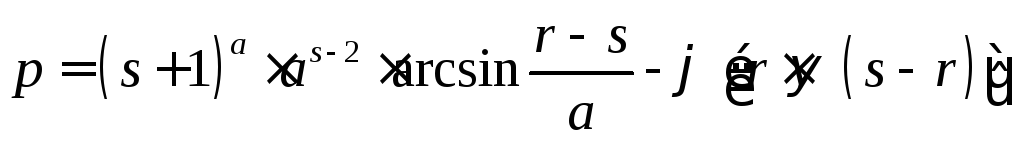
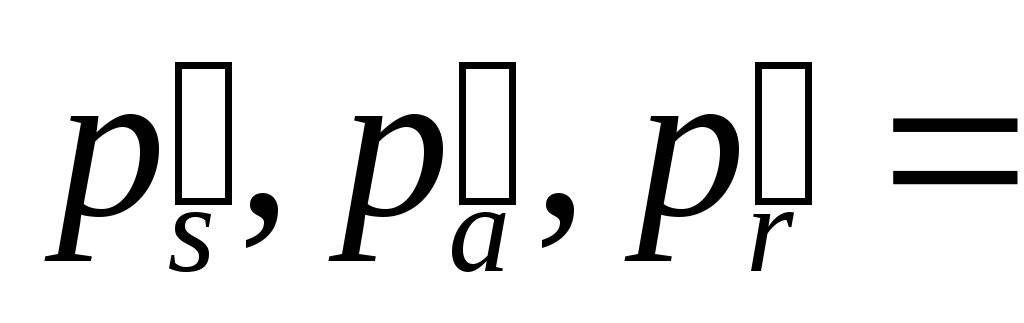


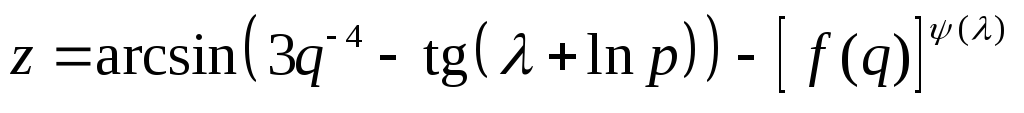
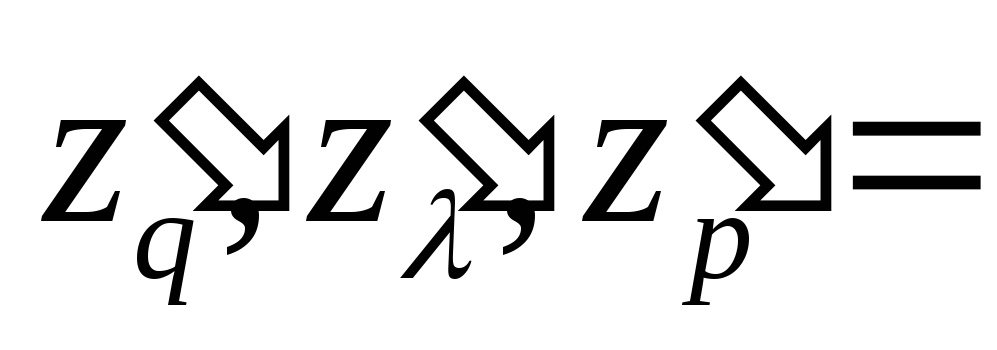

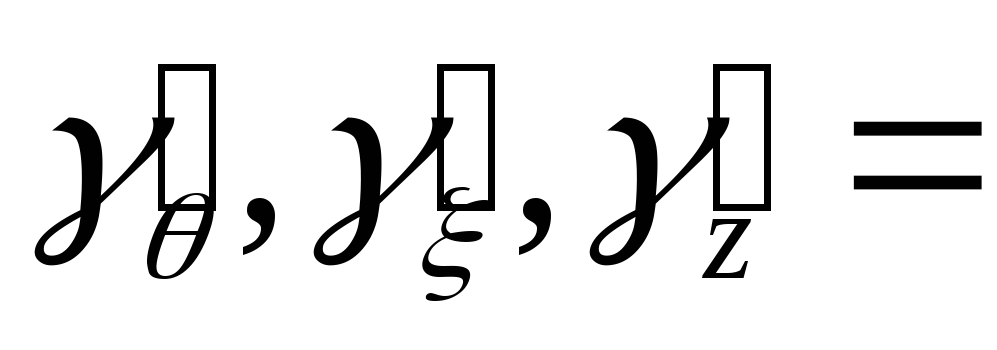

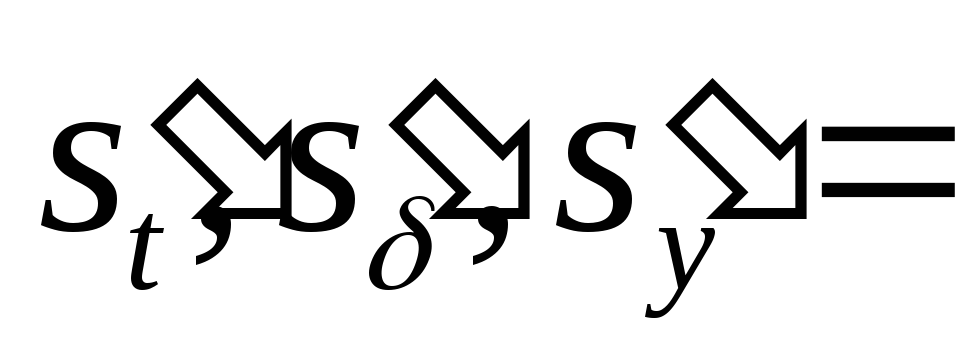


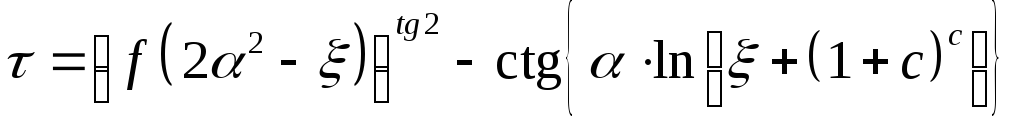

61

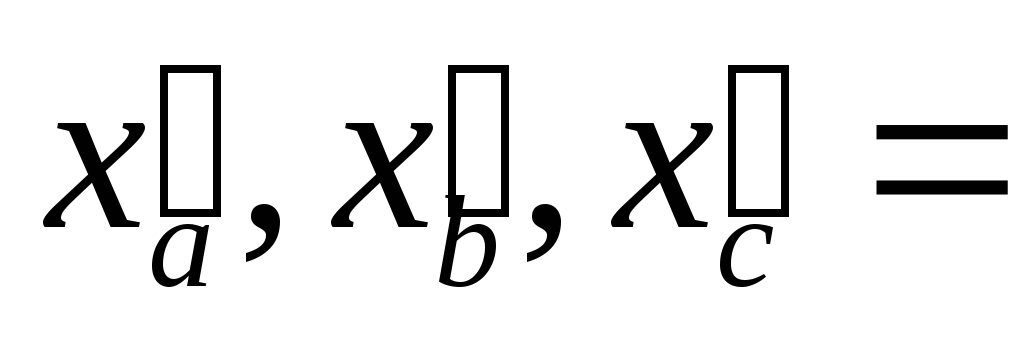
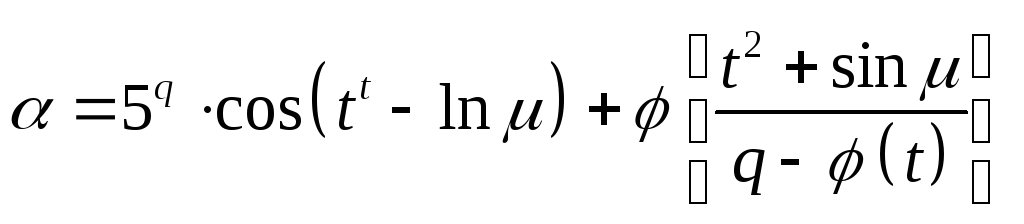
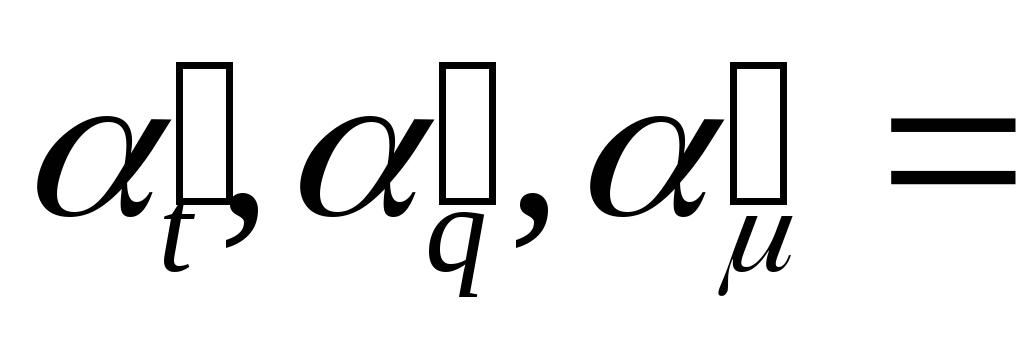


Контрольная работа № 13.
Доказательство неравенств.
Доказать, что на указанных множествах, выполнены следующие неравенства
1.
![]()
![]()
![]() .
.
2.
![]()
![]() .
.
3.
![]()
![]() .
.
4.
![]()
![]() .
.
5.
![]()
![]() .
.
6.
![]()
![]() .
.
7.

![]() .
.
8.
![]()
![]() .
.
9.
![]()
![]() .
.
10.
![]()
![]() .
.
11.
![]()
![]() .
.
12.
![]()
![]() .
.
62
13.
![]()
![]() .
.
