КВАНТЫ билеты / 7. Постулаты квантовой механики

Постулаты квантовой механики

Во введении было указано на принципиальное отличие квантовомеханического описания состояния физической системы от классического. Оно заключается в том, что в классической физике состояние объекта полностью определяется через его местоположение и импульс (скорость). В квантовой механике подобным способом описывать состояние микрообъекта невозможно, поскольку из-за его специфических свойств координаты и импульс не могут быть измерены одновременно, а, следовательно, и определены. В связи с этим возникла необходимость нового понимания того, как надо описывать квантовое состояние. Оно нашло отражение в первом из четырех постулатов, которые являются базой для квантово-механического подхода к изучению физических свойств реальных микросистем.

Постулат 1 сформулируем так: состояниям (имеем в виду чистые

состояния) произвольной квантовой системы, которая характеризуется неким набором физических величин (он зависит от природы системы), в любой момент времени сопоставляются кет-векторы, принадлежащие гильбертову пространству, называемому пространством состояний.

Первый постулат требует соблюдения основного принципа квантовой механики – принципа суперпозиции состояний. Он сводится к двум утверждениям:

а) если система может находиться в состояниях 1 и 2, описываемых соответственно векторами состояний g1 и g2 , то она может

находиться и в состоянии 3, которому ставится в соответствие вектор

будет описывать то же самое состояние.

Отметим, что величину, которая характеризует физическую систему в динамике, а не саму по себе (как, например, масса), иногда называют

физическую систему. В микромире взаимодействие с прибором (макрообъектом) существенно возмущает систему (микрообъект), что приводит к изменению ее состояния. Это означает, что до процедуры измерения состояние квантовой системы описывал один вектор состояния, а после измерения другой. Если обратится к языку математики, то процесс измерения выглядит как преобразование «старого» кет-вектора в «новый». В гл. 1 было сказано, что математическая операция, позволяющая сопоставить произвольному вектору новый вектор, называется оператором. Следовательно, в квантовой механике оператором можно изображать процесс измерения. А поскольку при измерении определяется значение динамической переменной, то можно считать, что оператор характеризует саму эту переменную. В связи с этим вводятся следующие два постулата.

Постулат 2: динамической переменной L сопоставляется опера-

тор ˆ , определенный на множестве векторов состояний из

L g

пространства состояний. Причем, чтобы не нарушался принцип суперпозиции, оператор должен быть линейным однородным.

Отметим, что в общем случае разные динамические переменные L и T

изображаются не коммутирующими друг с другом операторами ˆ и ˆ : ˆ ˆ

L T [L,T ]

≠ 0.

Постулат 3: результатом измерения динамической переменной L

может быть только такое число l, которое является собственным

значением соответствующего оператора ˆ .

L

Заметим, что при измерении физических величин получают вещественные числа, поэтому на изображающие их операторы требуется наложить определенные условия. А именно, операторы должны иметь вещественные собственные значения. Такими операторами, как известно, являются эрмитовые операторы.

Согласно постулатам 2 и 3, оператор ˆ динамической переменной L L

обладает такими свойствами. Во-первых, его спектр должен совпадать с набором численных значений соответствующей динамической переменной. Во-вторых, соотношения для оператора должны правильно передавать соотношения для динамической переменной, которую он изображает.

Следующий постулат говорит о вероятностном характере процесса измерения величин микрообъектов.

Постулат 4: при измерении динамической переменной L квантовой

системы, находящейся в чистом состоянии, которое описывается кетвектором g , получается одно из возможных собственных значений

оператора ˆ с определенной вероятностью.

L

Если кет-вектор нормирован на 1, а эрмитов оператор ˆ имеет g L

дискретный невырожденный спектр, то вероятность Pg(li) получить значение li находится по формуле

непрерывным невырожденным спектром, то вероятность dPg (l ) получить значение l , лежащее между l и l d , равна

Подчеркнем, что вероятность всегда действительна и положительна. Величина, равная квадрату модуля g (l ) -функции, называется

плотностью вероятности

g (l ) = g (l ) 2 ,

асама функция g (l ) , не

имеющая непосредственного физического смысла, играет роль амплитуды плотности вероятности. Поскольку плотность вероятности g (l )

экспериментально определяемая величина, она является однозначной функцией аргумента и не обращается в бесконечность (см. рис.2.1). Поэтому

и непрерывной. На эти свойства в дальнейшем будем часто ссылаться. Дадим несколько примеров физического толкования перечисленных

выше постулатов.

1) Пусть квантовая система находится в состоянии, которое описывается

собственным кет-вектором эрмитова оператора ˆ . Тогда результатом l L

измерения динамической переменной L обязательно будет число, равное

собственному значению l оператора ˆ , соответствующее кет-вектору

L l

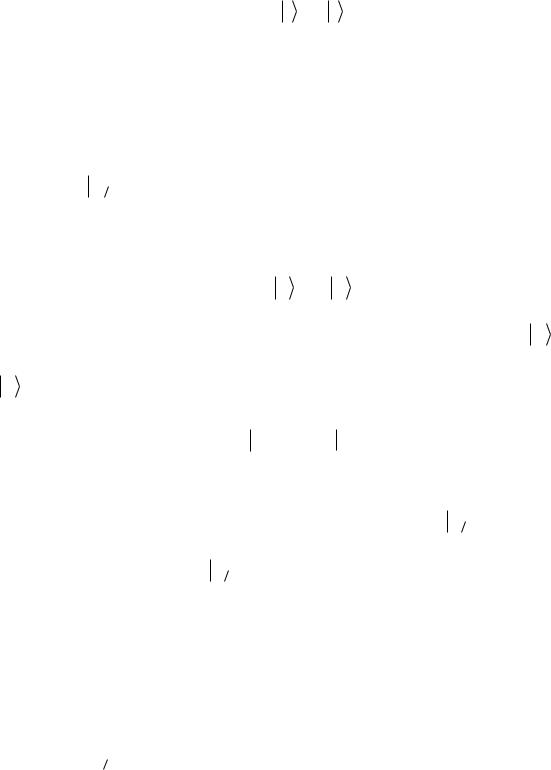
ˆ

L l = l l .

Такая ситуация относится к случаю, когда после процесса измерения динамической переменной физическая система остается в том же состоянии, что и до измерения. Хотя это не означает, что при акте измерения не было воздействия на систему.

2) Допустим, что процесс измерения динамической переменной L происходит в квантовой системе, которая находится в произвольном состоянии g . Для определенности считаем, что спектр эрмитова оператора

рассматривать как линейную комбинацию различных собственных векторов

li оператора ˆ

L

n

g = gi li .

i 1

При измерении динамической переменной L микросистема возмущается и переходит скачком в одно из собственных состояний li , соответствующих

значению li измеряемой величины L (извлекается из суперпозиции конкретное состояние li ). Следовательно, в результате измерения

получается с вероятностью Pg(li) одно из возможных собственных значений li

систему векторов в пространстве состояний. В этом случае любой кет-вектор

состояния выражается через собственные векторы оператора ˆ , которые g L

удовлетворяют соотношениям ортонормировки (1.17) и полноты базиса

(1.21), когда спектр оператора ˆ дискретен, или (1.18) и (1.30), когда спектр

L

– непрерывен.

Необходимо заметить, что одновременно могут быть измерены только те динамические переменные L и T, для которых изображающие их эрмитовы

математически доказывается, что операторы коммутируют, если они имеют общую полную систему собственных векторов.

Различные одновременно измеримые динамические переменные объединяются в так называемые полные наборы.