
mcad_pract
.pdf
ЗАДАНИЕ 3 Вычисление точек перегиба функции
Найти точку перегиба и интервалы выпуклости и вогнутости исходной функции на отрезке [-3,10]:
3.1Построить график функции второй производной f2 на ин-
тервале [-3, 10].
3.2Найти точку перегиба px, решая уравнение f ’’(x)=0 на ин-
тервале [-3,10].
3.3Убедиться, что найденные точки являются точками перегиба, анализируя знаки второй производной слева и справа от точки
перегиба (рх): f ’’(px+0.1) и f ’’(px-0.1).
3.4Точка перегиба делит заданный отрезок [-3,10] на два интер- вала:[-3,pх], [pх,10]. Анализируя знак производной на каждом интервале, определить, какой из них является интервалом выпуклости, а какой интервалом вогнутости. Записать в комментариях.
3.5Скопировать график функции второй производной f2, добавить в графический блок график функции f и отметить на графике исходной функции найденную точку перегиба маркером "х".
Вариант 1
ЗАДАНИЕ 4 Вычисление определенного интеграла
4.1Вычислить значение определенного интеграла функции y=- ex+3 на интервале [-2;1].
4.2Построить график функции этой же функции, на интервале [-2;1]. Отобразить на графике ось ОХ и установить сетку по обеим осям с шагом 1.
4.3На графике определить фигуру, площадь которой была вычислена в п.1.1, и, пользуясь клетками, подсчитать приблизительную ее площадь.
ЗАДАНИЕ 5 Определение площади фигуры, ограниченной графиком функции и осью ОХ, и длины дуги
5.1 Построить график функции y = 3x − x 2 + 1 и ось ОХ на ин-
тервале [-2,4].
5.2 Найти абсциссы точек пересечения функции с осью ОX, решая нелинейное уравнение. Отделение корней выполнить по графику.
80

5.3Используя определенный интеграл, найти площадь фигуры. Полученные абсциссы использовать в качестве пределов интегрирования.
5.4Найти длину дуги параболы y = 3x − x 2 + 1 на интервале [-
2,4].
ЗАДАНИЕ 6 Определение площади и периметра фигуры, ограниченной двумя функциями и осью ОХ
6.1 Построить графики функций y = −0.2x 2 + 5 , y=x-0.5 на ин-
тервале [-1,6]и добавить ось ОХ
6.2Найти абсциссы пересечения графиков функций с осью ОХ
6.3Найти абсциссу пересечения функций между собой, решая
нелинейное уравнение x − 0.5 = −0.2x2 + 5 с помощью функции root или решая систему двух нелинейных уравнений.
6.4Найти площадь фигуры, ограниченной этими функциями и осью ОХ.
6.5Найти периметр фигуры как сумму длин дуг функций и длины отрезка оси ОХ, ограниченного точками пересечения функций
сосью ОХ.
ЗАДАНИЕ 7 Определение площади и периметра фигуры, ограниченной двумя функциями
7.1 Построить графики функции y = −x2 + 4 и y=x2+2 на интер-
вале [-2,2].
7.2Найти абсциссы точек пересечения этих функций между со-
бой.
7.3Найти площадь фигуры, ограниченной этими функциями
a)как разность двух интегралов,
b)как двойной интеграл.
7.4Найти периметр фигуры, ограниченной этими функциями, как сумму длин дуг.
81

Вариант 2
ЗАДАНИЕ 4 Вычисление определенного интеграла
4.1 Вычислить значение определенного интеграла функции y = 2 sin x + 1 , на интервале [0;2].
4.2Построить график функции этой же функции, на интервале [0;2]. Отобразить на графике ось ОХ и установить сетку по обеим осям с шагом 1.
4.3На графике определить фигуру, площадь которой была вычислена в п.2.1, и, пользуясь клетками, подсчитать приблизительную ее площадь.
ЗАДАНИЕ 5 Определение площади фигуры, ограниченной графиком функции и осью ОХ
5.1 Построить график функции y = cos( x + 2 ) − 0.2 и ось ОХ на интервале [-5,1].
5.2Найти абсциссы точек пересечения функции с осью ОX, решая нелинейное уравнение. Отделение корней выполнить по графику.
5.3Используя определенный интеграл, найти площадь фигуры. Полученные абсциссы использовать в качестве пределов интегрирования.
5.4Найти длину дуги функции из п.2.1.
ЗАДАНИЕ 6 Определение площади и периметра фигуры, ограниченной двумя функциями и осью ОХ
6.1 Построить графики функций y = ex − 2 , y = −x 3 + 25 и
ось ОХ на интервале [1,3].
6.2Найти абсциссы пересечения графиков функций с осью ОХ
6.3Найти абсциссу пересечения функций между собой, решая
нелинейное уравнение − x 3 + 25 = ex − 2 с помощью функции root.
6.4Найти площадь фигуры, ограниченной этими функциями и осью ОХ.
6.5Найти периметр фигуры как сумму длин дуг функций и длины отрезка оси ОХ, ограниченного точками пересечения функций
сосью ОХ.
82

ЗАДАНИЕ 7 Определение площади и периметра фигуры, ограниченной двумя функциями
7.1 Построить графики функции y = x2 − 2 и y = 1 − 2x2 на от-
резке [-2,2].
7.2 Найти абсциссы точек пересечения этих функций между собой.
7.3 Найти площадь фигуры, ограниченной этими функциями а) как разность двух интегралов, б) как двойной интеграл.
7.4 Найти периметр фигуры, ограниченной этими функциями, как сумму длин дуг.
Задания для самостоятельной работы
В тетради для лабораторных работ написать последовательность выполнения действий.
1. |
Найти значение первой и второй производной выражения |
|||||||||
2cos(x)-1.5 для x=2. |
|
|
|
|
|
|
||||
2. |
Определить функцию |
|
2 |
|
|
|
|
|||
f(x)=2cos(x)-1.5 и функ- |
|
|
|
|
|
|
||||
ции |
ее |
первой f1(x) и |
f ( x) |
|
|
|
|
|
||
|
|
|
f2(x) |
производ- |
|
|
|
|
|
|
второй |
|
|
2 |
4 |
6 |
8 |
||||
ной. |
|
|
|
f1(x) |
|
|||||
|
|
|
|
|
|
|
|
|||
3. |
Для функции f(x): |
f2(x) |
2 |
|
|
|
|
|||
|
a) |
найти экстремумы |
|
|
|
|
||||
|
|
|
|
|
|
|
||||
и определить тип экстремума |
|
|
|
|
|
|
||||
на интервале [2;8] |
|
|
4 |
|
|
|
|
|||
|
b) |
найти точки пере- |
|
|
|
|
x |
|
||
гиба |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. |
Написать |
последовательность |
выполнения |
действий |
для |
|||||
вычисления: |
|
|
|
|
|
|
|
|||
|
a) |
площади фигуры, об- |
|
1 |
1 |
|
|
|
||
разованной функцией y=sin x и |
|
|
|
|
||||||
|
|
|
|
|
||||||
|
|
|
|
|
|
|||||
осью ОХ |
|
|
|
sin(x) |
|
|
|
|
||
- на отрезке [0;π], |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
||||
- на отрезке |
[0;3π/2], |
0 |
|
0 |
1.57 |
3.14 |
4.71 |
|||
|
|
|
|
|
|
|||||
- 1 1
0 |
x |
3× |
p |
|
|
|
|
|
|
2 |
|
83
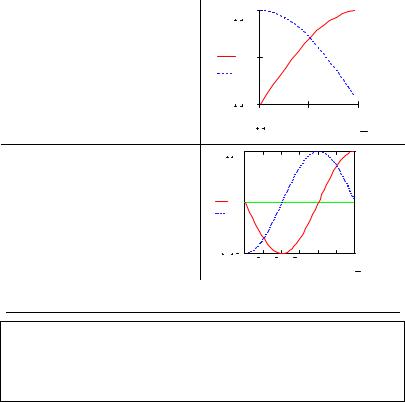
b) площади и периметра |
|
1 |
1 |
|
|
|
|
|
|
фигуры, образованной пересе- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
чением двух функций y=sin x, |
sin( x) |
|
|
|
|
|
|
|
|
y=cos x и осью ОХ на отрезке |
|
|
|
|
|
|
|
||
|
|
0.5 |
|
|
|
|
|
|
|
[0;π/2], |
cos(x) |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0.79 |
|
1.57 |
|
|
|
|
|
0 |
|
|
x |
|
π |
c) площади и периметра |
|
|
|
|
|
|
|
|
2 |
1 |
1 |
|
|
|
|
|
|
|
|
фигуры, образованной пересе- |
|
|
|
|
|
|
|
|
|
чением двух функций y=sin x, |
|
|
|
|
|
|
|
|
|
y=cos x, двумя способами: |
sin ( x) |
0 |
|
|
|
|
|
|
|
- через двойной интеграл; |
cos ( x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- через разность интегралов на |
|
|
|
|
|
|
|
|
|
отрезке [-3π/4; π/4]. |
− 1 |
1 |
|
|
|
|
|
|
|
|
|
2.36 |
1.57 |
0.79 |
0 |
0.79 |
1.57 |
||
|
|
3.14 |
|||||||
|
|
|
− π |
|
|
x |
|
|
π |
|
|
|
|
|
|
|
|
|
2 |
Задания для закрепления материала
Уравнение касательной к графику функции y= f(x) в точке (xо, yо)
имеет вид: |
y - y |
′ |
) × ( x - x0 |
) . Уравнение нормали к графику |
|||
0 = f ( x0 |
|||||||
функции y= f(x) в точке (xо, yо) имеет вид: y - y 0 |
= - |
x - x0 |
. |
||||
|
|||||||
|
|
|
|
|
|
f ¢( x0 ) |
|
1.Построить касательную и нормаль к графику функции f(x) в точке xo= 3, в следующем порядке:
2.задать значение x0 и вычислить соответствующее значение
y0.
a)определить функцию fk(x) – касательную в точке (x0,y0) и функцию fn(x) – нормаль в точке (x0,y0).
b)построить в одном графическом блоке графики исходной
функции, касательной и нормали на интервале [0,10]. Увеличить графический блок в два раза. Изменить предельные границы графического блока по оси OY на [-10,10].
84

3.Исследовать функцию:
Вариант - 1 |
|
Вариант - 2 |
|||||||||
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
x - |
|
|
|
|
|
x |
|
2 |
||
|
|
|
|||||||||
f ( x ) = -20 × |
|
|
7 |
|
|
|
|
|
|||
|
|
|
|
на ин- |
f ( x ) = cos 2x - |
|
на интер- |
||||
|
|
|
|
|
|||||||
|
|
|
2 |
|
|
|
|
2 |
|
|
|
x + |
|
|
|
|
|
|
|
|
|
|
|
1.1 |
|
вале [1, 3] |
|
|
|||||||
|
|
|
|
|
|
|
|||||
тервале [-1, 3]
−найти точку пересечения функции с осью Ох, решая уравнение f(x)=0.
−найти точку экстремума и определить тип экстремума,
−найти точку перегиба функции.
4.Найти площадь и периметр фигуры, ограниченной двумя функциями и, осью ОХ
|
Вариант - 1 |
|
|
|
|
Вариант - 2 |
|
|
|
||||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = 2e 2 - 1 и |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
x 3 |
|
|
|
|
|
|
|||||||
|
|
|
2 |
|
5 + x |
|
|
||||||||
4 |
|
|
y = 3 - |
|
|
, и y = |
x |
|
× |
|
|
- 1 на |
|||
|
|
5 - x |
|
5 - x |
|||||||||||
y = |
|
-1 |
|
|
|
|
|
|
|
|
|
|
|||
x + 3 |
интервале [0,3]. |
|
|
|
|
|
|
||||||||
на интервале [-2,2]. |
|
|
|
|
|
|
|
|
|
|
|
||||
Указание к выполнению:
a)Построить графики функций и ось OX на интерва-
ле
[-2,2].
b)Найти координаты точки пересечения функций, решая систему уравнений.
c)Найти точку пересечения первой функции с осью
OX и точку пересечения второй функции с осью OX, решая нелинейные уравнения.
d)Найти площадь фигуры, как сумму площадей фигур, образованных каждой функцией.
e)Найти периметр, как сумму длин дуг функций и
длины отрезка.
85

5. Найти площадь |
и периметр фигуры, ограниченной двумя |
||||
функциями и осью OX. |
|
|
|||
Вариант - 1 |
|
|
Вариант - 2 |
||
y = |
|
и y = x2 |
|
53 |
|
x + 1 |
y = |
и y = 3sin( x − 1.5) + 5 на |
|||
на интервале [-1,2] |
52 + x 2 |
||||
интервале [-3,3]
Указание к выполнению:
a)Построить графики функций и ось ОХ.
b)Найти координаты точек пересечения функций, дважды решая систему уравнений с разными начальными приближениями корней.
c)Вычислить площадь фигуры:
d)как разность площадей верхней и нижней фигуры
(первый способ),
e)используя двойные интегралы (второй способ).
f)Вычислить периметр фигуры, как сумму длин дуг.
Контрольные вопросы
1.Геометрический смысл определенного интеграла.
2.Вычисление определенного интеграла функции, выражения.
3.Точность вычисления определенного интеграла.
4.Что может быть использовано в качестве пределов интегрирования?
5.Вычисление площади фигуры, образованной пересечением двух функций и осью ОХ.
6.Вычисление интеграла по области. Примеры.
7.Вычисление площади фигуры, образованной пересечением двух функций: с использованием интеграла по области, с использованием разности двух определенных интегралов
8.Вычисление длины дуги. Использование длины дуги для определения периметра фигуры, заданной одной или несколькими функциями.
86
Образец контрольной работы по теме "Производные и интегралы"
ЗАДАНИЕ 1
1.1 Вычислить с точностью 0,00001 для выражения 4 cos2 3x следующие значения:
a)первую производную для х1=-2. Результат вывести на экран, не занося в переменную.
b)вторую производную для х2=3. Результат занести в переменную Pr2.
c)вычислить определенный интеграл на интервале [2;4].
ЗАДАНИЕ 2
2.1 Задать исходную функцию f(x) для вычисления выражения из пункта 1.1.
2.2 Найти площадь фигуры, образованной исходной функцией над осью ОХ на интервале [π/2,5π/6], предварительно вычисляя точки пересечения функции с осью (решая уравнение).
2.3 Найти длину дуги L исходной функции над осью ОХ по формуле.
b
L = ∫  1+ (f / ( x ))2 dx a
1+ (f / ( x ))2 dx a
ЗАДАНИЕ 3
4
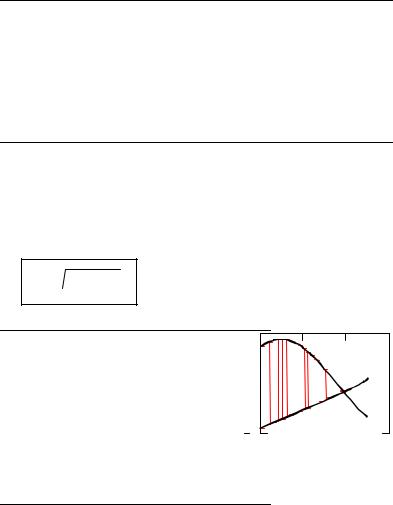
3.1 |
Определить функцию g( x ) = 7 − x2 . |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f(x) |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Построить графики исходной функции |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
f(x) и g(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xr |
|
|
||
3.2 |
Найти точку |
пересечения двух |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
функций (xr), решая |
систему уравне- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g(x) |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
ний. |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3.3 |
Используя двойной интеграл, |
|
|
|
2.2 |
|
|
|
|
|
|
|
|
|
|
|
2.4 |
2.6 |
|||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
найти площадь фигуры, ограниченной по оси ОУ функциями f(x) и g(x), по оси ОХ значениями 0.5 и xr.
ЗАДАНИЕ 4
4.1Определить функции первой и второй производной для выражения из пункта 1.1.
4.2Найти экстремумы исходной функции на интервале [π/2, π]:
87

a)решить уравнение f '(x)=0, отделяя корни графическим способом.
b)вычислить значение второй производной в каждой точке экстремума. В комментариях написать тип экстремума.
c)отметить на графике исходной функции точки экстрему-
ма.
Тема 13 Интерполяция
Цель работы – научить студента вычислять значения функции, заданной таблично для аргумента, отсутствующего в таблице, c использованием линейной интерполяции.
ЗАДАНИЯ
ЗАДАНИЕ 1 Линейная интерполяция
Между гибкостью λ и коэффициентом f продольного изгиба цен- трально-сжатых элементов из стали с расчетным сопротивлением Ry=200 Па имеется табличная зависимость вида (табл. 72 СНИП II23 81*"Стальные конструкции"):
λ |
|
10 |
20 |
30 |
40 |
50 |
60 |
70 |
|
80 |
90 |
100 |
110 |
f |
|
0.988 |
0.967 |
0.939 |
0.906 |
0.869 |
0.827 |
0.782 |
|
0.734 |
0.665 |
0.599 |
0.537 |
|
|
1.1 Найти коэффициенты продольного изгиба f1 и f2 централь- |
|||||||||||
|
но-сжатых элементов с гибкостью λ1=34 и λ2=86, используя ли- |
||||||||||||
|
нейную интерполяцию. Ответ: 0.926, 0.693. |
|
|
|
|
|
|||||||
|
|
1.2 Отобразить на графике: исходные вектора f и λ в виде от- |
|||||||||||
|
дельных точек, соединенных между собой, |
и точки с координата- |
|||||||||||
|
ми (λ1, f1), (λ2, f2), |
|
|
|
|
|
|
|
|
|
|||
88
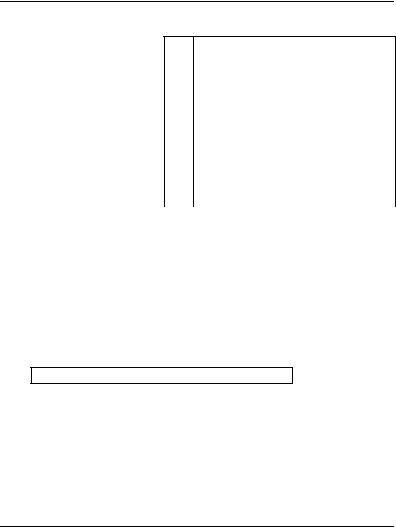
ЗАДАНИЕ 2 Линейная интерполяция по таблице
Для расчета колонн с неподвижно опертым верхним концом используется таблица ко-
эффициентов μ, завися- |
β |
|
|
|
n |
|
|
|
|
щая от β и n: β = J2 / J1, n |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
0.6 |
0.7 |
||
|
|||||||||
= L2 / L1, где |
0.04 |
1.02 |
1.84 |
2.25 |
2.59 |
2.85 |
3.08 |
3.24 |
|
L1 - длина подкрановой |
|
|
|
|
|
|
|
|
|
0.06 |
0.91 |
1.47 |
1.93 |
2.26 |
2.57 |
2.74 |
2.9 |
||
части колонны; |
|
|
|
|
|
|
|
|
|
0.08 |
0.86 |
1.31 |
1.73 |
2.05 |
2.31 |
2.49 |
2.68 |
||
L2 - длина надкрановой |
|||||||||
|
|
|
|
|
|
|
|
||
0.1 |
0.83 |
1.21 |
1.57 |
1.95 |
2.14 |
2.33 |
2.46 |
||
части колонны; |
|||||||||
J1 - момент инерции под- |
0.2 |
0.79 |
0.98 |
1.23 |
1.46 |
1.67 |
1.85 |
2.02 |
|
крановой части колонны; |
|
|
|
|
|
|
|
|
|
0.3 |
0.78 |
0.9 |
1.09 |
1.27 |
1.44 |
1.6 |
1.74 |
||
J2 - момент инерции над- |
|
|
|
|
|
|
|
|
|
0.4 |
0.78 |
0.88 |
1.02 |
1.17 |
1.32 |
1.45 |
1.58 |
||
крановой части колонны. |
|||||||||
|
|
|
|
|
|
|
|
||
Значения β хранятся в файле B.txt, значения n – |
в файле N.txt, таб- |
||||||||
лица коэффициентов μ - в файле M.txt. Файлы находятся в папке с заданиями для лабораторных работ.
Найти коэффициенты μ для следующих вариантов исходных данных:
a)L1=400 см, L2=160 см, J1=121570 см4, J2=18235.5 см4
b)L1=400 см, L2=180 см, J1=98340 см4, J2=9834.2 см4
c)L1=400 см, L2=168 см, J1=80040 см4, J2=9604.8 см4
2.1Прочитать значения векторов B, N и матрицы M из файлов, используя функцию:
имя_вектора:=READPRN("путь к файлу")
2.2Для каждого из вариантов a), b), c):
d)найти β и n по формулам,
e)вычислить искомое значение μ обращением к функции линейной интерполяции.
f)проверить визуально правильность вычисленного значения, сравнивая с табличными значениями.
Ответ: a) μ = 1.705, b) μ = 2.045, c) μ = 1.891
Задания для самостоятельной работы
Втетради для лабораторных работ выполнить задания.
1.Записать последовательность действия для вычисления значения таблично заданной функции для x=2.4, x=7
x |
1 |
3 |
4.5 |
5 |
y |
10 |
13 |
17 |
20 |
89
