
Brunbender_Elektromagnetizm_2012
.pdf
Запишем уравнение (12.1) в более компактной форме |
|
q 2βq ω2q 0 . |
(12.2) |
0 |
|
Уравнение (12.2) имеет решение
|
q q (0)e βt cos(ωt |
0 |
), |
(12.3) |
|
m |
|
|
|
где qm(0) – амплитуда колебаний в начальный момент времени; |
коэф- |
|||
фициент затухания; |
круговая (циклическая) частота колебаний. |
|
||
В идеальном случае (R = 0) коэффициент затухания |
= 0, колебания |
|||||||||||
становятся незатухающими и происходят по гармоническому закону |
||||||||||||
|
|
|
|
q qm cos(ω0t |
0 ) , |
(12.4) |
||||||
где ω0 |
|
1 |
|
– круговая частота собственных колебаний в контуре при |
||||||||
|
|
|
||||||||||
|
|
|
||||||||||
LC |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||
отсутствии затухания. Период гармонических колебаний |
|
|||||||||||
|
|
|
|
|
2π |
|
|
|
|
|
|
|
|
|
|
|
T0 |
2π |
LC. |
(12.5) |
|||||
|
|
|
|
ω0 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
||
Для неидеального контура (R ≠ 0) частота колебаний уменьшается с |
||||||||||||
ростом коэффициента затухания по закону |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
ω |
|
ω2 |
β2. |
(12.6) |
||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
В случае сильного затухания ( ω2 |
β2 ) наблюдается разряд конденсатора |
|||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
||
по цепи контура без возбуждения колебаний; такой процесс называют апе-
риодическим. При слабом затухании ( ω2 |
β2 ) частота колебаний в контуре |
0 |
|
близка к 0 ; такие колебания похожи на гармонические, но отличаются от них тем, что их амплитуда уменьшается во времени. Затухающие колебания такого вида и будут изучаться в данной работе.
Характеристики затухающих колебаний в контуре |
|
|
Амплитуда qm уменьшается во времени по закону |
|
|
q |
q (0)e βt. |
(12.7) |
m |
m |
|
Время релаксации 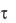 – время, за которое амплитуда колебаний умень-
– время, за которое амплитуда колебаний умень-
|
qm (t) |
e |
|
1 |
|
шается в е раз |
|
τ |
β . |
(12.8) |
|
q (t τ) |
|||||
|
m |
|
|
|
|
Время релаксации обратно пропорционально коэффициенту затухания.
Число колебаний N в контуре за время релаксации |
|
||||
Nτ |
τ |
|
1 |
. |
(12.9) |
T |
|
||||
|
|
βT |
|
||
Логарифмический декремент затухания  равен натуральному логарифму отношений двух амплитуд через период колебаний
равен натуральному логарифму отношений двух амплитуд через период колебаний
λ ln |
qm (t) |
βT |
λ 1 Nτ . |
(12.10) |
||
qm (t |
T ) |
|||||
|
|
|
|
|||
71
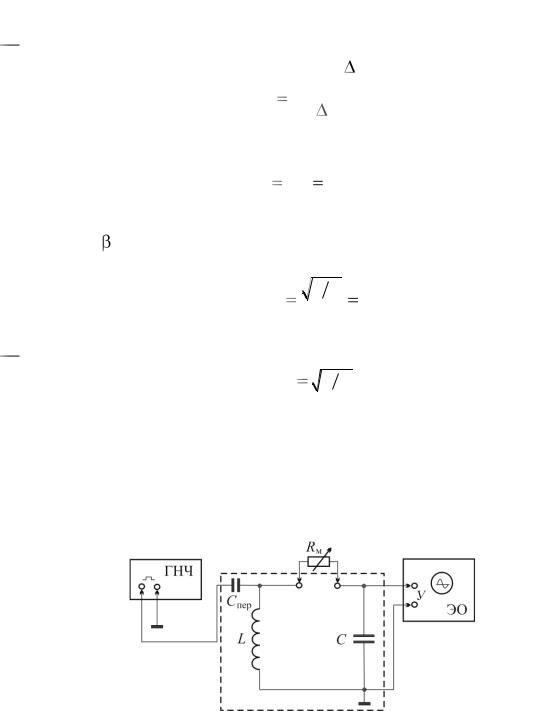
Логарифмический декремент затухания обратно пропорционален N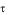 .
.
Добротность контура Q пропорциональна отношению энергии колебаний W(t) в данный момент к ее изменению W за период колебаний Т:
Q 2π W (t) . |
(12.11) |
W |
|
Для рассматриваемого случая слабого затухания формула для расчета добротности приводится к виду
Q |
π |
πNτ. |
(12.12) |
|
|
||||
βT |
||||
|
|
|
Добротность пропорциональна числу колебаний за время релаксации. Выразив и Т через значения R, L, C контура, получим формулу расче-
та добротности по параметрам контура
Q |
|
L C |
RВ , |
(12.13) |
|
R |
|||
|
|
R |
|
где RВ – волновое сопротивление контура. Волновое сопротивление
|
|
|
(12.14) |
RВ L C, |
|||
в отличие от активного сопротивления контура уменьшает затухание колебаний в контуре.
Методика эксперимента
1. Схема опыта.
Рис. 12.2. Электрическая схема опыта:
ГНЧ – низкочастотный генератор; Спер – переходной конденсатор; L – катушка индуктивности; С – конденсатор; Rм – магазин сопротивлений; ЭО – электронный осциллограф. Пунктиром показаны элементы, размещенные на схемной плате
2. Возбуждение электромагнитных колебаний в контуре.
Исследуемый в работе колебательный контур состоит из катушки индуктивности L, конденсатора С и магазина сопротивлений Rм, с помощью которого можно изменять активное сопротивление контура R. Возбуждение контура производится под воздействием импульсного напряжения, по-
72
даваемого на контур через переходной конденсатор Спер от генератора низкочастотных электрических колебаний. При возбуждении в контуре колебаний напряжение на конденсаторе С изменяется пропорционально заряду q, то есть по закону затухающих колебаний
U |
C |
U |
C(m) |
(0)e βt |
cos(ωt |
0 |
), |
(12.15) |
|
|
|
|
|
|
где UC(m)(0) = qm(0)/C – амплитудное значение напряжения на конденсаторе в начальный момент времени. Напряжение с конденсатора подается на вход «у» электронного осциллографа. Колебания светящегося пятна на экране осциллографа происходят по закону изменения напряжения на входе «у» осциллографа, то есть осциллограф позволяет визуально исследовать зависимость Uc(t) при возбуждении электромагнитных колебаний в цепи контура.
3. Определение периода и циклической частоты колебаний.
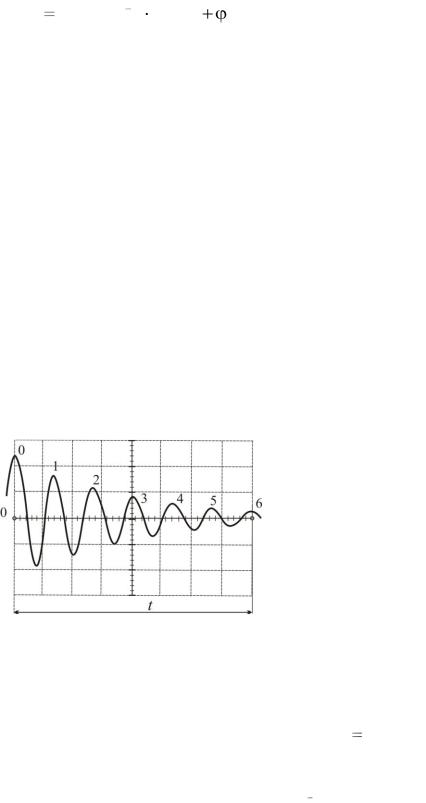
При помощи ручки « » осциллографа установите картину затухающих колебаний симметрично горизонтальной оси х (оси времени). При правильной установке “хвост” картины колебаний должен совместиться с осью х. При помощи переключателя шкалы времени «TIME/DIV» («мс/дел») получите на экране осциллографа 8-10 полных колебаний (ручка плавной регулировки шкалы времени должна быть установлена в крайнее правое положение). Ручкой « » осциллографа совместите наибольший (нулевой) максимум положительной полярности с начальным левым вертикальным делением шкалы осциллографа (см. рис. 12.3).
Рис. 12.3. Примерный вид картины затухающих колебаний на экране осциллографа: (N = 6, nx = 8)
Отсчитайте N ~ (7-10) максимумов и по оси х определите их время следования t = схnx (сх – цена деления по оси х; nx – число делений по оси х для N
колебаний). Рассчитайте период T = t/N и циклическую частоту ω |
2π |
. |
|
||
|
Т |
|
В качестве примера рассчитаем период и циклическую частоту колебаний по рис. 12.3. Пусть на переключателе «TIME/DIV» установлена цена деления сх = 0,5 мс/дел. Время 6 колебаний t = 0,5 мс/дел · 8 дел = 4 мс = 4·10 3 с. Находим пе-
73
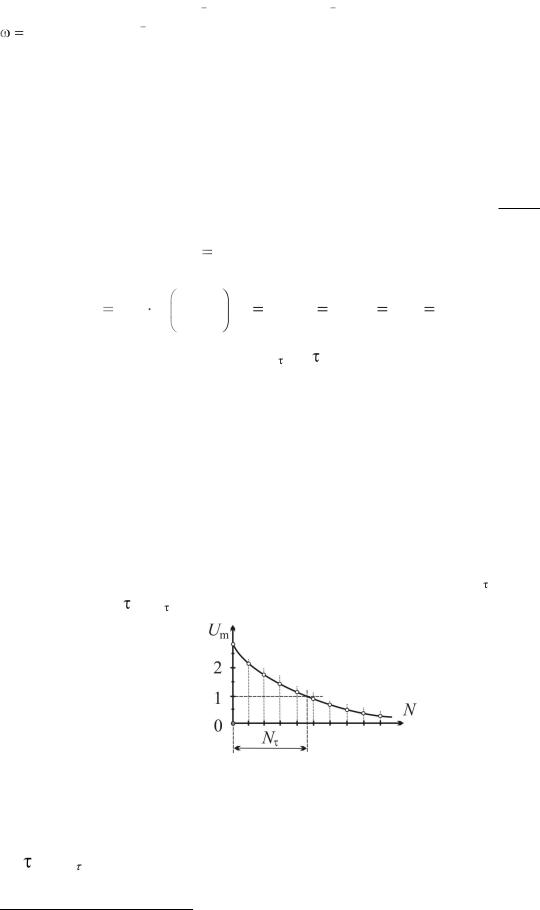
риод колебаний Т = 4·10 3 с/ 6 = 0,67·10 3 с. Циклическая частота колебаний
6,28 рад/ 0,67·10 3 с = 9,42·10 3 рад/ с.
4. Определение характеристик затухающих колебаний по 2 измерениям.
При помощи регулятора выходного напряжения ГНЧ и переключателя «В/дел» осциллографа установите наибольшую (в пределах шкалы «у» осциллографа) амплитуду нулевого максимума. Ручкой « » осциллографа совместите N-й максимум (см. пункт 3 методики измерений) с осью «у» шкалы осциллографа и измерьте (в делениях шкалы у) его амплитуду*.
Найдите отношение амплитуд нулевого и N-го максимумов: Um (0) .
Um (t)
Учтем, что t = NT, |
Um (0) |
|
βt |
откуда |
|
|
|
|
|
|
||||||||
|
|
|
e |
|
|
|
|
|
|
|
||||||||
|
Um (t) |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
β |
1 |
ln |
Um (0) |
|
; τ |
1 |
|
; |
Nτ |
|
τ |
; Q πNτ |
π |
. |
(12.16) |
|||
NT |
Um (t) |
|
β |
T |
βT |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
5. Определение N |
|
и |
по графику Um(N). |
|
|||||||||||||
Ручкой « » осциллографа совместите наибольший (нулевой) максимум положительной полярности с осью «у» шкалы осциллографа. При помощи регулятора выходного напряжения ГНЧ установите амплитуду нулевого максимума равной 2,7 дел по шкале «у». Ручкой « » осциллографа совместите первый максимум с осью «у», измерьте по шкале «у» его амплитуду, затем аналогично измерьте амплитуду второго, третьего и так далее максимумов. По данным измерений постройте график зависимости амплитуды колебаний (в делениях оси у) от количества колебаний Um(N). По графику определите точку, в которой кривая Um(N) пересекается с прямой у = 1, и определите число колебаний за время релаксации N . Время релаксации из (12.9) = N ·Т.
Рис. 12.4. Примерный график зависимости Um(N)
6. Расчет сопротивления контура.
Согласно пунктам 3, 4, 5 методики эксперимента (при Rм = 0) определите
Т, , и N . По формуле (12.12) рассчитайте Q. Увеличьте сопротивление контура на величину Rм. По картине затухающих колебаний (п. 4, 5) опре-
* Амплитуда N-го максимума должна быть не менее 0,4 дел. шкалы.
74

делите ', по формулам (12.9) и (12.12) рассчитайте N ' и Q' соответствен-
но. Для рассмотренных случаев согласно (12.13) можно получить систему уравнений, из которых находится формула для расчета сопротивления контура R:
Q |
RВ |
; Q |
RВ |
|
|
||
|
R |
R Rм |
|
R |
Q Rм |
. |
(12.17) |
|
|||
|
Q Q |
|
|
Волновое сопротивление контура рассчитывается по формуле RВ = QR (при Rм = 0). Формулы для расчета емкости С и индуктивности L контура
могут быть получены из (12.5) и (12.14): |
|
|
|
|||
C |
T |
; |
L |
TRВ . |
(12.18) |
|
2πR |
||||||
|
|
|
2π |
|
||
|
В |
|
|
|
|
|
Порядок выполнения работы
Перед включением в сеть установите:
на ГНЧ ручку регулятора выходного напряжения в крайнее левое положение, переключатель «форма сигнала» в положение «прямоугольный
импульс», переключатель «частота» в положение « 10», ручку плавной
регулировки частоты в положение «20-30 дел»; на осциллографе – переключатель рода сигнала в положение «~»,
чувствительность «y» в положение «0,5 В/дел», «TIME/DIV» в положение
«0,1 мс/дел»;
на магазине сопротивлений установите все ручки в положение «0». Убедившись в правильности собранной схемы, с разрешения препода-
вателя включите приборы.
Задание 1. Изучение зависимости Q(R).
1. Согласно п. 3 методики эксперимента измерьте период колебаний Т, рассчитайте циклическую частоту колебаний .
2. Согласно п. 4 методики измерений определите коэффициент затухания , проверьте выполнение условия слабого затухания ω2 β2. Рассчитайте добротность контура Q. Данные занесите в табл. 12.1
Данные занесите в табл. 12.1
Таблица 12.1
Rм (Ом)
/с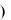
Q
3. Установите на магазине сопротивление Rм = 100-200 Ом. Согласно методике измерений определите и Q. Проведите аналогичные измерения, увеличивая Rм через 100-150 Ом. Данные занесите в табл. 12.1
4. По данным измерений постройте график зависимости Q(Rм).
75

Задание 2. Определение параметров контура.
1. Согласно п. 3 методики эксперимента измерьте период колебаний Т, рассчитайте циклическую частоту колебаний .
2. Согласно п. 5 методики измерений снимите данные Um(N), внесите их в табл. 12.2.
Таблица 12.2
Номер |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
максимума |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||
Амплитуда |
2,7 |
|
|
|
|
|
|
|
|
|
|
|
(дел) |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
По данным эксперимента постройте график Um(N). По графику определите число колебаний N , рассчитайте время релаксации 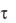 и коэффициент затухания . Проверьте выполнение условия слабого затухания ω2 β2 . Рас-
и коэффициент затухания . Проверьте выполнение условия слабого затухания ω2 β2 . Рас-
считайте число колебаний за время релаксации N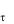 и добротность Q.
и добротность Q.
3. Установите на магазине сопротивление Rм ~ 150-200 Ом. Согласно п. 5 методики измерений снимите данные U'm(N), внесите их в таблицу, подобную 12.2. Постройте график U'm(N). По графику U'm(N) определите N ' , рассчитайте ' и Q' .
4. Согласно п. 6 методики эксперимента рассчитайте активное сопротивление контура R и его волновое сопротивление RВ. По формулам (12.18) рассчитайте емкость С и индуктивность L цепи контура.
Контрольные вопросы
1.Колебательный контур, возбуждение электромагнитных колебаний в цепи контура, преобразование энергии при электромагнитных колебаниях.
2.Условия установления гармонических колебаний, слабого затухания
иапериодического процесса в цепи колебательного контура.
3.Причина затухания колебаний в контуре, уравнения затухающих ко-
лебаний, характеристики затухающих колебаний: 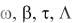 N
N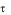 Q.
Q.
4.Волновое сопротивление контура, его связь с параметрами контура.
5.Зависимость добротности контура от величины волнового и активного сопротивлений контура.
Список литературы
1.Савельев И. В. Курс общей физики: учеб. пособие для втузов: в 5 кн. Кн. 2. Электричество и магнетизм. – М.: Астрель, 2003. – С. 310–317.
2.Детлаф А. А., Яворский Б. М. Курс физики: учеб. пособие для вузов.
–М.: Высш. шк., 1999. – С. 371–0374.
2.Трофимова Т. И. Курс физики: учеб. пособие для вузов. – М.: Высш.
шк., 2003. – С. 267–271.
76

Лабораторная работа № 2.13
ИЗУЧЕНИЕ РЕЗОНАНСА В ЦЕПИ КОЛЕБАТЕЛЬНОГО КОНТУРА
Цели работы: измерение резонансной частоты электромагнитных колебаний в цепи колебательного контура; расчет индуктивности контура; расчет добротности контура по параметрам резонансной кривой; экспериментальная оценка влияния коэффициента затухания контура на амплитуду напряжения при резонансе.
Приборы и принадлежности: плата с закрепленной электрической монтажной схемой колебательного LC контура; генератор низкочастотных электрических колебаний (звуковой генератор – ЗГ); магазин сопротивлений Rм; электронный вольтметр с цифровым отсчетом (ЭВ).
Теория работы
Собственные электромагнитные колебания в контуре
Электрическим колебательным контуром называется цепь, состоящая из последовательно включенных конденсатора С, катушки индуктивности L и активного сопротивления* R. Электромагнитные колебания в контуре можно возбудить с помощью кратковременного внешнего электромагнитного воздействия. В процессе колебаний в контуре происходит перекачка
энергии электрического поля конденсатора Wэ |
CU 2 |
|||||
|
в энергию магнитно- |
|||||
2 |
||||||
|
|
|
|
|
||
го поля катушки Wм |
LI |
2 |
и наоборот. При протекании тока в цепи контура |
|||
|
|
|||||
2 |
|
|||||
|
|
|
|
|
||
выделяется тепловая мощность P = I2R, что приводит к потере электромагнитной энергии и затуханию колебаний. В общем случае собственные колебания в контуре описываются уравнением
q q (0)e βt |
cos(ωt |
0 |
), |
(13.1) |
m |
|
|
|
где q – заряд конденсатора; qm(0) – амплитудное значение заряда в началь-
ный момент времени; β |
R |
|
коэффициент затухания; = 2 |
– цикли- |
|||||
2L |
|||||||||
|
|
|
|
|
|
|
|||
ческая частота колебаний, |
– частота колебаний, 0 – начальная фаза ко- |
||||||||
лебаний. |
|
|
|
|
|
|
|
||
В идеальном случае (при R = 0) колебания в контуре являются незату- |
|||||||||
хающими и происходят по гармоническому закону |
|
||||||||
|
|
|
|
|
q |
qm cos(ω0t 0 ) , |
(13.2) |
||
где ω0 |
|
1 |
|
круговая частота собственных незатухающих колебаний. |
|||||
|
|
|
|||||||
|
|
|
|||||||
LC |
|||||||||
|
|
|
|
|
|
|
|
||
Наиболее важными характеристиками контура являются коэффициент
* Сопротивление R имеет любой контур, находящийся в нормальном (несверхпроводящем) состоянии, обычно R распределено по всей цепи контура.
77

|
|
|
|
|
|
|
|
|
|
|
затухания |
; циклическая частота колебаний ω ω2 |
β2 ; период колеба- |
||||||||
|
|
|
0 |
|
|
|
||||
ний T = 2 / |
; добротность (для случая слабого затухания ω2 |
β2 ) |
||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q |
π |
|
|
L C |
. |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
βT |
|
|
R |
|
|
|
||
Возбуждение вынужденных колебаний
При включении в цепь колебательного контура генератора электрических колебаний (рис. 13.1), ЭДС которого изменяется по гармоническому закону
г (t) г(m) cos(ωt), (13.3)
в цепи контура возникнут электромагнитные колебания. В уравнении (13.3) г(m) – амплитудное значение ЭДС генератора.
Рис. 13.1. Генератор электрических колебаний в цепи колебательного контура
В момент замыкания ключа в цепи контура одновременно возникнут два типа колебаний – собственные затухающие колебания с частотой соб и
вынужденные колебания с частотой генератора |
. Амплитуда собственных |
|
колебаний уменьшается во времени по экспоненциальному закону |
||
q |
(t) q (0)e βt |
, |
соб |
соб |
|
и через некоторое время* собственные колебания прекратятся. Вынужденные колебания происходят по гармоническому закону с час-
тотой генератора :
q qm cos(ωt ), |
(13.4) |
где qm – амплитудное значение заряда на конденсаторе,  – фазовый сдвиг между колебаниями заряда на конденсаторе и ЭДС генератора.
– фазовый сдвиг между колебаниями заряда на конденсаторе и ЭДС генератора.
В работе исследуются установившиеся вынужденные колебания, происходящие в контуре после затухания собственных колебаний.
Расчет амплитуды вынужденных колебаний
Запишем второй |
закон Кирхгофа для цепи колебательного |
контура |
||||
(рис. 13.1) в некоторый момент времени t: |
|
|||||
|
|
|
|
г(t) + (t) = U(t) + UR(t), |
(13.5) |
|
где (t) = |
L |
dI |
LI |
Lq – ЭДС самоиндукции в катушке; U(t) = q/C – |
||
dt |
||||||
|
|
|
|
|
||
* Время установления колебаний.
78

напряжение на конденсаторе; UR(t) = IR = Rq – напряжение на активном
сопротивлении; q – заряд конденсатора; I – сила тока в контуре; R – полное активное сопротивление цепи контура; точками над символами обозначены производные по времени. После преобразований (13.5) получим дифференциальное уравнение второго порядка
q 2βq ω2q |
г(m) |
cos(ωt) . |
(13.6) |
|
|||
0 |
L |
|
|
|
|
||
Одним из решений этого уравнения является уравнение вынужденных колебаний (13.4). Найдем первую и вторую производные ( q, q ) от заряда по
времени и после подстановки в (13.6) и несложных преобразований полу-
чим |
q |
ω2 cos(ωt |
) q ω2 cos(ωt |
) 2q βωsin(ωt ) |
г(m) |
cos(ωt). |
|
||||||
|
m |
0 |
m |
m |
L |
|
|
|
|
|
|
||
С точки зрения теории колебаний найденное выражение означает, что алгебраическая сумма трех колебаний (в левой части выражения) равна колебанию в правой части. Для сложения колебаний воспользуемся векторной диаграммой (при  < 0).
< 0).
Рис. 13.2. Векторная диаграмма колебаний (для t = 0)
Из |
векторной |
диаграммы (рис. |
13.2) |
|
согласно теореме |
Пифагора: |
||||||||||||||||||
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
г(m) |
q |
2 |
2 |
2 |
4q |
2 |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω |
ω |
|
|
β |
ω ,откуда найдем амплитудное значение заряда |
||||||||||||||||
|
|
|
|
|
||||||||||||||||||||
|
L |
m |
0 |
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
qm |
|
|
|
|
|
г(m) / L |
|
|
. |
|
|
(13.7) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ω2 |
|
ω2 |
|
4β2ω2 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
||||
|
Амплитуда напряжения на конденсаторе Um = qm/C, откуда |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
Um |
|
|
|
|
г(m) /(LC) |
|
. |
(13.8) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω2 |
ω2 |
|
4β2ω2 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
Резонанс напряжений
Анализ формулы (13.8) показывает, что зависимость Um( ) имеет максимум в интервале частот 0 < 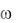 < . При
< . При 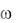 < 0 с ростом частоты знаме-
< 0 с ростом частоты знаме-
натель дроби уменьшается, что приводит к возрастанию Um; при |
> 0 |
79
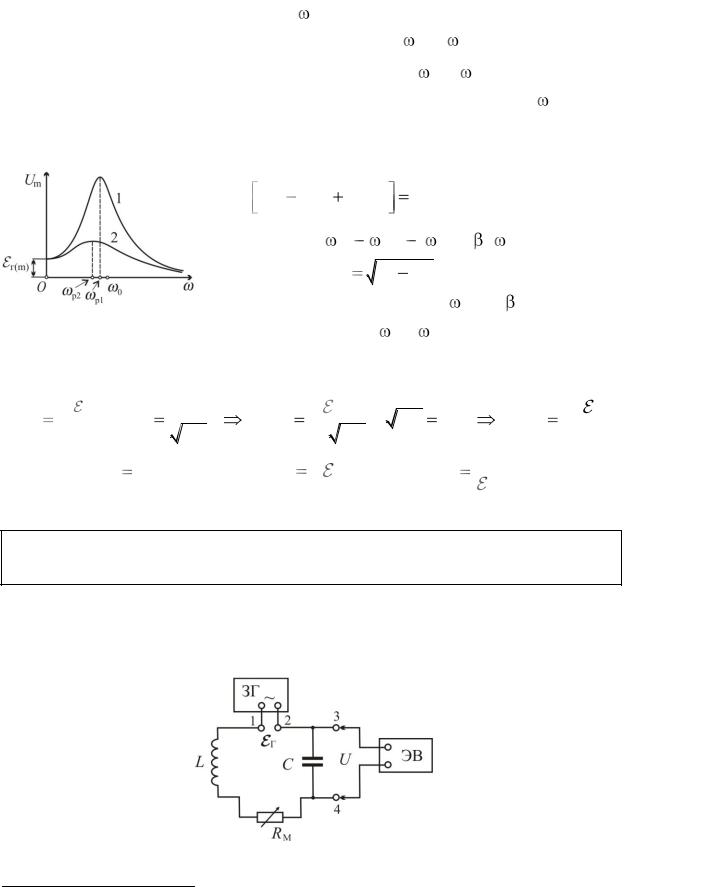
с ростом частоты знаменатель увеличивается, при этом Um уменьшается. Примерный график зависимости Um( ) дан на рис. 13.3. Из графика видно,
что максимальное значение Um наблюдается при |
|
|
|
0. Явление возрас- |
|
|||||||||||||||||||||||||||||
тания амплитуды напряжения на конденсаторе при |
|
0 |
называют резо- |
|
||||||||||||||||||||||||||||||
нансом напряжений. Найдем резонансную циклическую частоту |
р мето- |
|
||||||||||||||||||||||||||||||||
дом дифференцирования. В точке максимума производная от выражения, |
|
|||||||||||||||||||||||||||||||||
находящегося в знаменателе под корнем, равна нулю*. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
d |
|
ω2 |
ω2 2 |
|
4β2ω2 |
0 | |
|
|
|
|
|
. |
|
|
(13.9) |
|
|||||||||
|
|
|
|
|
|
|
|
|
dω |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
при ω=ωр |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из (13.9): 2( |
02 |
|
|
2) ( 2 |
) + 8 |
|
2 |
2 = 0 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω |
|
ω2 |
2β2 . |
|
|
|
|
|
|
(13.10) |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
р |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
В случае слабого затухания |
02 » 2 |
|
2, при этом |
|
||||||||||||||||||||||
Рис. 13.3. Резонансные кривые |
|
|
|
|
|
|
|
|
р |
0. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
С помощью формул (13.8) и (13.10) можно найти амплитудное значение |
|
||||||||||||||||||||||||||||||||
напряжения при резонансе для случая слабого затухания: |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
г(m) |
|
|
1 |
|
|
|
|
|
|
|
г(m) |
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
2π г(m) |
|
|||
U |
m(р) |
; ω |
|
|
|
|
U |
m(р) |
|
|
|
; |
|
LC |
|
|
|
|
|
U |
m(р) |
. |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
2βω0 LC |
0 |
|
LC |
|
|
2β |
|
LC |
|
|
|
|
|
|
|
2π |
|
|
|
|
2βT |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Поскольку |
π |
|
Q, получим |
Um(р) |
|
Q г(m) , откуда |
|
|
Q |
|
Um(р) |
. |
|
(13.11) |
|
|||||||||||||||||||
βT |
|
|
|
|
|
|
|
г(m) |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из (13.11) следует физический смысл Q при вынужденных колебаниях.
Добротность контура показывает, во сколько раз амплитуда напряжения на конденсаторе при резонансе больше амплитуды ЭДС генератора.
Методика эксперимента
Схема опыта
Рис. 13.4. Электрическая схема изучения электромагнитного резонанса
* Исследуемое подкоренное выражение при этом будет иметь минимальное значение. 80
