
Геометрия / Задания (плоскость)
.pdf
А.Н. РОМАНОВ
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
Сборник заданий
Омск - 2007
Факультет компьютерных наук Кафедра кибернетики
А.Н. РОМАНОВ
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
Сборник заданий по аналитической геометрии на плоскости предназначен для студентов, изучающих дисциплину "Геометрия". Сборник содержит задания для самостоятельного решения, а так же
примеры выполнения заданий.
Омск - 2007
УДК 514.12 ББК 22.151я73
С232
Романов А.Н.
С232
Аналитическая геометрия на плоскости. Сборник заданий. – Омск: Изд-во КАН, 2007. – 26 c.
Сборник заданий предназначен для проведения работ со студентами специальностей 220100, 075200 по курсу ¾Геометрия¿.
УДК 514.12 ББК 22.151я73
Рекомендовано к изданию учебно-методической комиссией и ученым Советом факультета компьютерных наук ОмГУ.
Оглавление
Тема 1.
Прямоугольные и полярные координаты 5
Тема 2.
Преобразование прямоугольных координат 8
Тема 3.
Расстояние между точками на плоскости.
Деление отрезка в данном отношении |
12 |
Тема 4. |
|
Скалярное произведение векторов |
14 |
Тема 5. |
|
Уравнение прямой на плоскости |
18 |
Тема 6. |
|
Кривые второго порядка |
21 |
4

Прямоугольные и полярные координаты |
5 |
|
|
Тема 1
Прямоугольные и полярные координаты
Задание: Определить местоположение на плоскости точек A; B; C; заданных полярными координатами. Найти декартовы координаты этих точек. На чертеже обозначить координатные оси и найденные точки.
y
A C x
B
Прямоугольные и полярные координаты.
Пример вычисления.
A(1; ¼=6); B(2; ¡¼=6); C(4; 0)

6 |
Тема 1. |
1. Определим местоположение точек на плоскости:
A(1; ¼=6) - первая четверть;
B(2; ¡¼=6) - четвертая четверть;
C(4; 0) - первая четверть
2. Определим декартовы координаты точек, используя формулы преобразования полярных координат в декартовы:
½
X = R ¤ cos(') Y = R ¤ sin(')
Получаем:
p
A(1 ¤ cos(¼=6); 1 ¤ sin(¼=6)) = A( 3=2; 1=2)
p
B(2 ¤ cos(¡¼=6); 2 ¤ sin(¡¼=6)) = B(2 3=2; ¡1)
C(4 ¤ cos(0); 4 ¤ sin(0)) = C(4; 0)
Прямоугольные и полярные координаты |
7 |
|
|
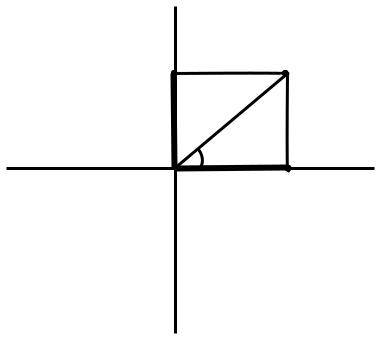
y
A
y=Rsin(a) R
a
x
x=Rcos(a)
Определение прямоугольных координат. Варианты заданий:
1.A(1; ¼); B(2; ¼=6); C(4; ¼=3)
2.A(2; ¼); B(2; ¼=2); C(4; ¼=3)
3.A(1; ¼=2); B(2; 2¼=3); C(0; ¼=3)
4.A(5; ¼=2); B(2; ¼=6); C(4; ¡¼=3)
5.A(1; ¡¼); B(2; ¼=6); C(2; ¼=3)
6.A(3; ¡¼=2); B(2; ¼=3); C(4; ¡¼=3)
8 |
Тема 2. |
7.A(1; 5¼=6); B(2; ¡¼=6); C(4; ¼=3)
8.A(1; ¼); B(4; ¡¼=6); C(2; ¡2¼=3)
9.A(2; ¡¼=2); B(3; ¡¼=6); C(4; ¼)
10.A(1; ¡¼); B(4; ¡2¼=3); C(1; ¼=6)
11.A(1; 0); B(2; ¼=6); C(4; ¡¼=3)
12.A(4; ¼); B(2; 0); C(4; 2¼=3)
13.A(3; 3¼=2); B(2; ¼=6); C(4; 0)
14.A(1; ¼=2); B(2; ¡¼=6); C(4; ¡2¼=3)
15.A(3; 0); B(2; ¡2¼=6); C(4; ¼=3)
16.A(¡1; ¡2¼); B(1; ¼=3); C(4; ¡¼=6)
17.A(3; ¡3¼=2); B(4; ¡¼=3); C(1; ¡2¼=3)
18.A(¡1; 5¼=3); B(1; ¡2¼=6); C(5; ¡¼=3)
19.A(3; ¡¼); B(¡2; 2¼=6); C(¡2; 4¼=3)
20.A(¡2; ¡¼=2); B(1; ¡5¼=6); C(¡4; 2¼)
21.A(3; ¡3¼); B(1; ¼=4); C(1; ¡¼=6)
Тема 2
Преобразование прямоугольных координат
Задание: В прямоугольных координатах дано уравнение прямой a: Известно, что уравнение записано в новых координатах, которые были получены

Преобразование прямоугольных координат |
9 |
|
|
из старых координат с помощью двух преобразований координатной системы: переноса начала координат по осям Ox и Oy на величины A и B соответственно и поворот координатных осей вокруг (уже перенесенного) начала координат на угол ® против часовой стрелки. Требуется найти уравнение прямой a в начальной (еще не преобразованной) координатной системе.
ay
B
y‘
x‘
x
A
Преобразование прямоугольных координат.
Пример вычисления.
a : 2x0 + 3y0 ¡ 1 = 0; A = 2; B = 1; ® = ¼4
1. Используемые формулы:

10 |
Тема 2. |
Напомним, что при преобразовании координатной системы (x; y) в (x0; y0) сами точки и фигуры на плоскости не изменяются, а изменяется лишь их координатное представление.
При этом старые координаты выражаются через новые следующим образом:
½x ¡ A = x0 cos ® ¡ y0 sin ® y ¡ B = x0 sin ® + y0 cos ®
Новые координаты через старые выражаются следующим образом:
½x0 = (x ¡ A) cos ® + (y ¡ B) sin ® y0 = ¡(x ¡ A) sin ® + (y ¡ B) cos ®
Внашем случае, при подстановке начальных данных во вторую группу формул, получим следующий вид для выражения новых координат через старые:
( y0 |
= ¡(x ¡ 2) sin |
4 |
+ (y ¡ 1) cos |
4 |
= ¡ p2 |
|||||||
x0 |
= (x |
¡ |
2) cos ¼ + (y |
¡ |
1) sin ¼ |
= x+y |
¡2 |
|
|
|||
|
|
4 |
|
|
4 |
|
p2 |
|||||
|
|
|
|
¼ |
|
|
|
¼ |
|
x+y+1 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
2. Найдем уравнение прямой a в новой координатной системе:
Для этого просто подставим полученные нами выражения для координат (x0; y0) в начальное уравнение прямой a: Получим:
2 x+y¡2 + 3 ¡x+y+1 ¡ 1 = 0
p p
2p2
¡x + 5y ¡ (1 + 2) = 0
Это и выражение будет являться уравнением прямой a в начальной системе координат. Видно, что
