
- •Саратовский государственный технический университет электричество и магнетизм 2
- •Саратов 2006
- •Лабораторная работа 1
- •Основные теоретические положения
- •Экспериментальная установка и методика измерений
- •Расчет погрешностей
- •Лабораторная работа 2
- •Основные теоретические положения
- •Обработка результатов
- •Расчет погрешностей
- •Лабораторная работа 3 изучение процессов заряда и разряда конденсатора
- •Основные теоретические положения
- •Экспериментальная установка и методика измерений
- •Обработка результатов
- •Расчет погрешностей
- •Лабораторная работа 4
- •Основные теоретические положения
- •Экспериментальная установка и методика измерений
- •Расчет погрешностей
- •Лабораторная работа 5
- •Основные теоретические положения
- •Экспериментальная установка и методика измерений
- •Расчет погрешностей
- •Лабораторная работа 6
- •Основные теоретические положения
- •Экспериментальная установка и методика измерений
- •Литература
- •Основные методики расчета погрешностей
- •Коэффициенты Стьюдента cn
Расчет погрешностей
Погрешность определения коэффициента передачи для цепи, содержащей два резистора, оценить по формуле:
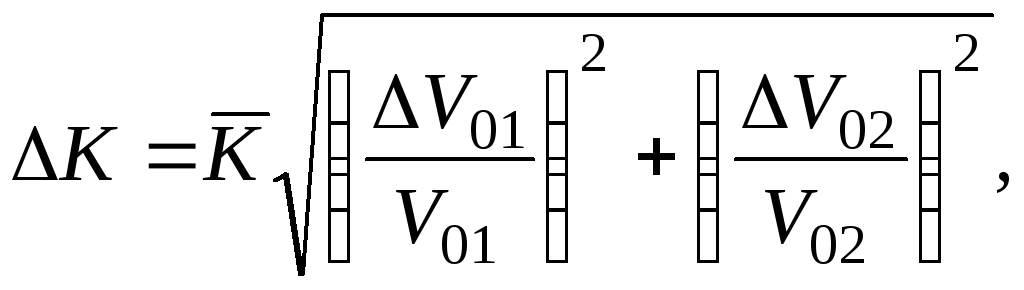
где
![]() .
Здесь учтено, что в нормальных условиях
применения осциллографа погрешность
измерения напряжения
.
Здесь учтено, что в нормальных условиях
применения осциллографа погрешность
измерения напряжения
![]() не
превышает 5%.
не
превышает 5%.
Погрешность
косвенных измерений
![]()
![]()
Погрешность измерения С определить, суммируя случайную и приборную погрешность, по (П.11):
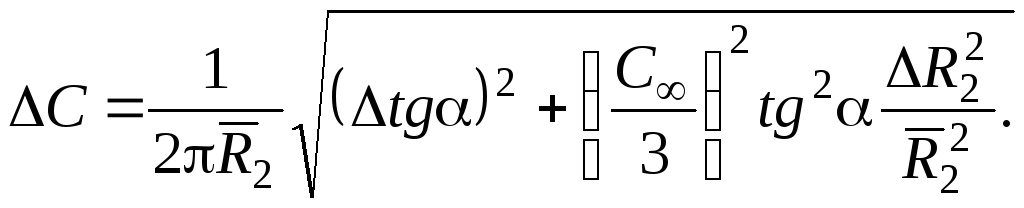
Погрешность
определения углового коэффициента
![]() подсчитать как погрешность линеаризации
методом наименьших квадратов (приложение),
считая
подсчитать как погрешность линеаризации
методом наименьших квадратов (приложение),
считая![]() ,
а
,
а![]() .
Результат представить в виде:
.
Результат представить в виде:
![]() .
.
Погрешность измерения L определить, суммируя случайную и приборную погрешность, по (П.11):
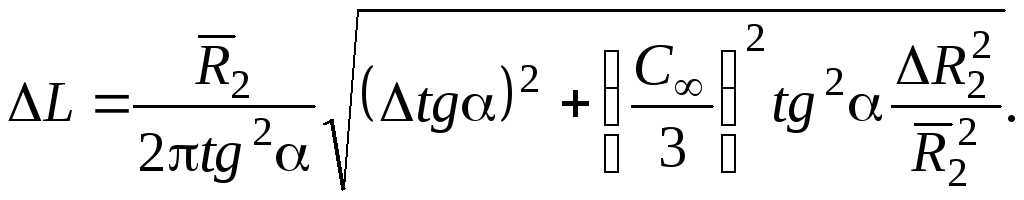
Погрешность
определения углового коэффициента
![]() подсчитать как погрешность линеаризации
методом наименьших квадратов (приложение),
считая
подсчитать как погрешность линеаризации
методом наименьших квадратов (приложение),
считая![]() ,
а
,
а![]() .
Результат представить в виде:
.
Результат представить в виде:![]() .
.
Лабораторная работа 5
ИССЛЕДОВАНИЕ ЗАТУХАЮЩИХ КОЛЕБАНИЙ
В КОЛЕБАТЕЛЬНОМ КОНТУРЕ
Цель работы: изучение параметров и характеристик колебательного контура.
Основные теоретические положения
Е
Рис.
5.1.
Колебательный
контур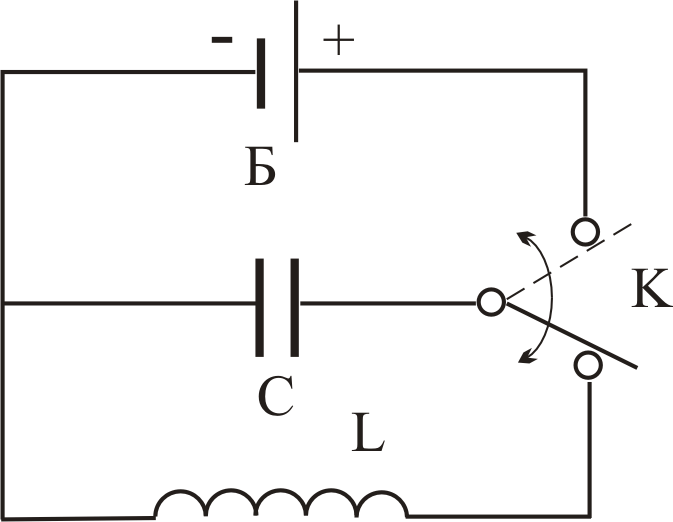
В
начальный момент, когда конденсатор
полностью заряжен, в нем
накоплена
электрическая энергия:
![]() .
Во время разряда конденсатора электрическая
энергия превращается в энергию магнитного
поля катушки и, когда конденсатор
полностью разряжен, вся электрическая
энергия переходит в магнитную:
.
Во время разряда конденсатора электрическая
энергия превращается в энергию магнитного
поля катушки и, когда конденсатор
полностью разряжен, вся электрическая
энергия переходит в магнитную:
![]()
![]() ,
,
где
![]() наибольшая величина тока в контуре.
наибольшая величина тока в контуре.
При перезаряде конденсатора энергия магнитного поля снова превращается в энергию электрического поля. В контуре возникают незатухающие электромагнитные колебания.
Проводники контура всегда обладают электрическим сопротивлением, поэтому часть энергии в процессе колебаний расходуется на нагрев проводников. Вследствие этого амплитуда электромагнитных колебаний в контуре постепенно уменьшается, и в нем происходят затухающие колебания (рис. 5.2). При достаточно большом сопротивлении контура или малой индуктивности колебания в нем вообще не возникают, а происходит так называемый апериодический разряд конденсатора (рис. 5.3).
 По
второму закону Кирхгофа можно записать:
По
второму закону Кирхгофа можно записать:
![]() ;
(5.1)
;
(5.1)
![]() .
(5.2) Так как
.
(5.2) Так как
![]() ,
то из
соотношения (5.2)
получаем:
,
то из
соотношения (5.2)
получаем:
![]()
![]() .
(5.3)
.
(5.3)
Подставив (5.3) в (5.1), получим:
![]() (5.4)
(5.4)
Как известно, дифференциальное уравнение (5.4) описывает затухающие колебания. Его решение имеет вид:
![]() ,
(5.5)
,
(5.5)
где
![]() коэффициент затухания:
коэффициент затухания:
![]() .
(5.6)
.
(5.6)
Циклическая частота затухающих колебаний определяется по формуле:
![]() (5.7)
(5.7)
при этом
![]() и
и
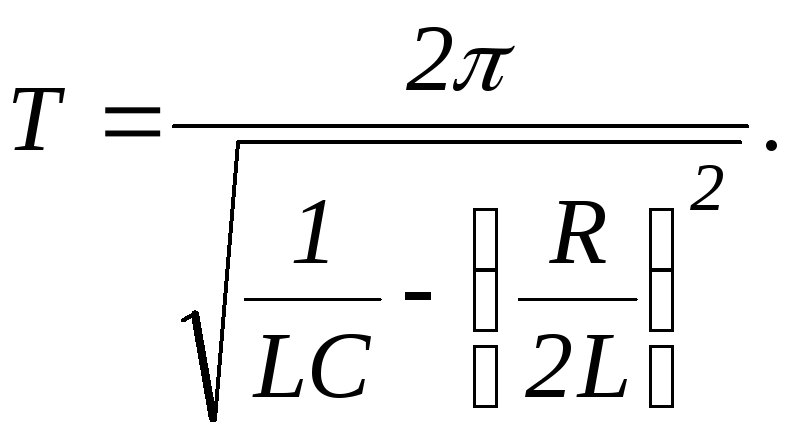 (5.7')
(5.7')
Если
(5.1) записать в виде
![]() и продифференцировать по времени, то
получим уравнение того же типа, что и
уравнение (5.4):
и продифференцировать по времени, то
получим уравнение того же типа, что и
уравнение (5.4):![]() из чего следует, что ток в контуре
совершает затухающие колебания, для
которых значения,
и Т
определяются
по (5.6), (5.7) и (5.7').
из чего следует, что ток в контуре
совершает затухающие колебания, для
которых значения,
и Т
определяются
по (5.6), (5.7) и (5.7').
Из
(5.7) и (5.7') следует, что в контуре возможны
затухающие колебания лишь в том случае,
если
![]() (частота и период – действительные
величины) или
(частота и период – действительные
величины) или![]() .
Если
.
Если![]() ,
то частота и период
мнимые, колебаний нет, и происходит
апериодический разряд конденсатора
(см. рис. 5.3).
,
то частота и период
мнимые, колебаний нет, и происходит
апериодический разряд конденсатора
(см. рис. 5.3).
Сопротивление
![]() (5.8)
(5.8)
называется критическим.
Для характеристики степени затухания колебаний, кроме коэффициента затухания , используется еще логарифмический декремент затухания.
Логарифмическим декрементом затухания колебаний называется натуральный логарифм отношения двух значений напряжения, разделенных интервалом времени, равным периоду колебаний:
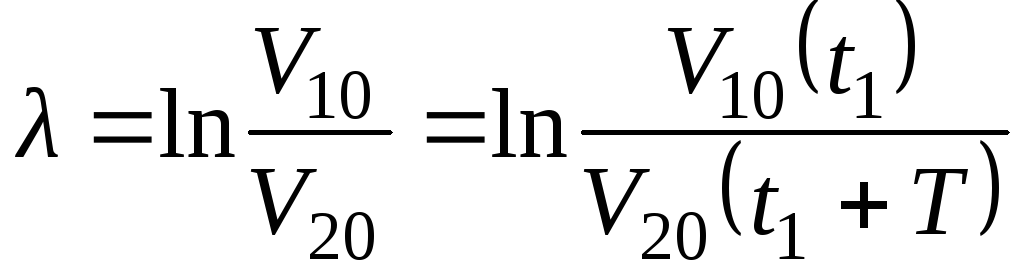 (5.9)
(5.9)
или
![]() .
(5.9')
.
(5.9')
Подставим
в (5.9) значения
![]() и
и![]() ,
получим:
,
получим:
![]() (5.10)
(5.10)
или согласно выражению (5.6)
![]() .
(5.10')
.
(5.10')
В
Рис.
5.4. Фазовая кривая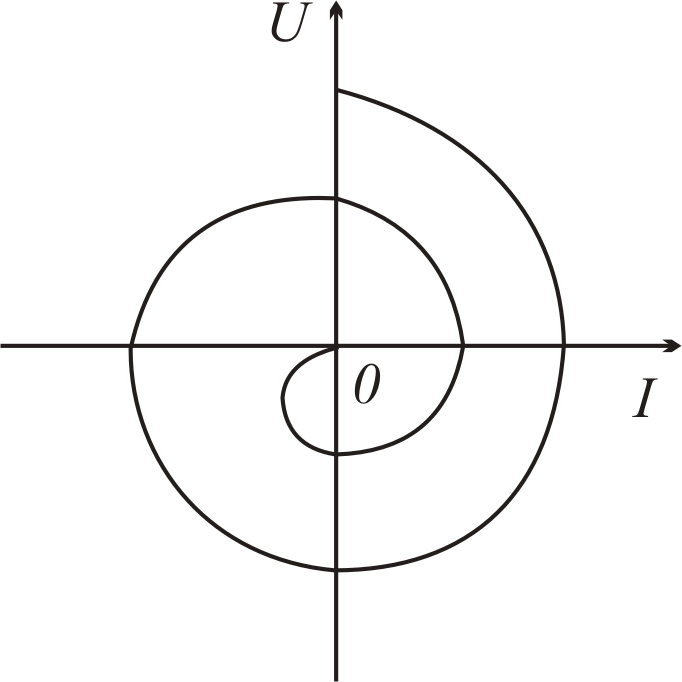
напряжение
на конденсаторе в тот же момент времени.
Плоскость
![]() I
носит название плоскости состояния или
фазовой плоскости, а кривая, изображающая
зависимость напряжения от тока, называется
фазовой кривой (рис.
5.4).
I
носит название плоскости состояния или
фазовой плоскости, а кривая, изображающая
зависимость напряжения от тока, называется
фазовой кривой (рис.
5.4).
Найдем
фазовую кривую для контура, сопротивление
которого R=0.
В этом случае
![]() ,
и из (5.5), (5.7) и (5.7') имеем:
,
и из (5.5), (5.7) и (5.7') имеем:
![]() и
и
![]() ;
(5.11)
;
(5.11)
![]() ;
;
![]() .
(5.12)
.
(5.12)
Уравнения (5.12) описывают незатухающие колебания. Исключив из них время t, получим уравнение фазовой кривой:
![]() .
.
Это уравнение эллипса. Эллипс получается в результате сложения двух взаимно-перпендикулярных гармонических колебаний (5.12), сдвинутых по фазе на четверть периода. В контуре, сопротивление которого R>0, происходят затухающие колебания напряжения (5.5) и тока:
![]() .
(5.13)
.
(5.13)
В этом случае амплитуды напряжения и тока в контуре непрерывно
убывают, не повторяясь через период времени, и фазовая кривая получается незамкнутой (рис. 5.4).
