gos_mast_final_2 / 3 / m_Строймех

Строительная механика

1. Метод определения внутренних усилий в упругих системах – метод сечений (РОЗУ).

Так как внутренние силы взаимно уравновешены и стоит задача выразить их через внешние, то необходимо выполнить такую операцию, чтобы внутренние силы стали явными.

Например для стержня можно применить прием мысленного рассечения на две части плоскостью, перпендикулярной продольной оси. Затем отбросить одну из полученных частей, что позволяет превратить внутренние силы, для целого стержня, во внешние для оставленной части стержня.

1. Рассекаем.

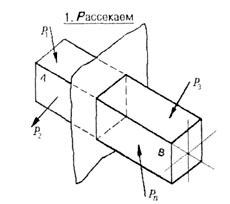
Силы взаимодействия будут в каждой точке проведенного сечения.

Эту систему большого числа сил по правилам теоретической механики можно привести к одной точке (центру тяжести поперечного сечения), в результате чего получим главный вектор R и главный момент М.

2. Отбрасываем отсеченную часть (левую или правую).

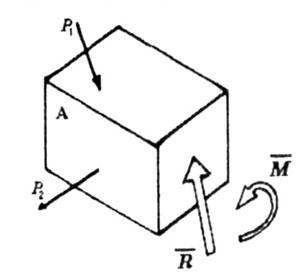
Теперь спроецируем на три оси (продольную z и две взаимно-перпендикулярные поперечные х и у). В результате получим шесть внутренних силовых факторов: три силы N, Qx Qy и три момента Мx, My и Мz.

Сила N называется продольной силой, силы Qx и Qy - поперечные силы. Момент относительно оси z - Мz - крутящий момент; и моменты Мx, My относительно поперечных осей - изгибающие.

Каждому из внутренних усилий соответствует определенный вид деформации (изменение формы), бруса. Например, продопьной силе N соответствует растяжение (или сжатие) бруса.

3. Заменяем

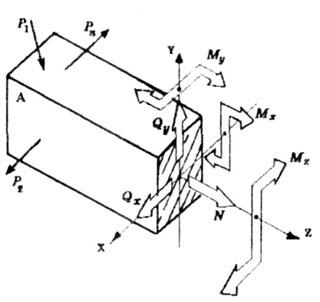
Таким образом, рассматривается одна из полученных при рассечении частей стержня, которая нагружена приложенными к этой части внешними силами и шестью внутренними усилиями (рис. 1.8).

4. Уравновешиваем

Для установления связи внутренних и внешних сил можно к этой части применить уравнения равновесия, (уравновешиваем), так как известно, что если тело находится в целом в равновесии, то в равновесии и любая его часть.

2.1. Обобщенная формула Максвелла-Мора для определения перемещений в плоских стержневых системах (балки, рамы, фермы).

где ∆кр- искомое перемещение в стержневой системе по направлению К от причины Р – внешней максимальной нагрузки;

n – максимальное количество участков, на которое разбивается система при построении эпюр внутренних усилий;

li – длина i-го участка;

Mp, Qp, Np – грузовые эпюры внутренних усилий на i-м участке, построенные от действия внешней нагрузки Р;

Mк, Qк, Nк – единичные эпюры внутренних усилий на i-м участке, построенные от действия общей единичной нагрузки Рк=1, приложенной в месте и направлении искомого перемещения;

k – безразмерный коэффициент, зависящий от формы поперечного сечения (при =1,2; I=1,16);

EI, GF, EF – изгибная, сдвиговая, осевая жесткости i-го участка;

Первое слагаемое в скобках – для расчета балок и рам, третье – для расчета ферм, первое и третье в сумме – для расчета арок.

Например, для ферм:

2.2. Правило Верещагина.

Применимо для балок, рам и арок.

При вычислении интегралов вместо аналитических выражений моментов используются их эпюры. Т.е. значение ∆кр можно найти по способу Верещагина, перемножив эпюры Мp и Мк.

Перемножить две эпюры - значит площадь нелинейной эпюры изгибающих моментов умножить на ординату другой обязательно линейной эпюры, находящейся под центром тяжести первой, и результат разделить на жесткость (в случаях, когда на данном участке обе эпюры линейны, совершенно безразлично, на какой из них брать площадь, а на какой ординату).

где  - площадь произвольной фигуры;

Мc - ордината прямолинейной эпюры, соответствующей центру тяжести площади 

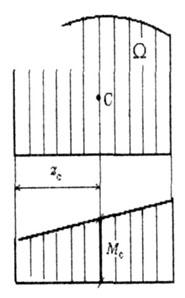(с – центр тяжести эпюры)

Другими словами, интеграл Мора решается следующим образом:

3. Сущность расчета статически неопределимых систем методом сил.

1. Определяем степень статической неопределимости системы по формуле Коперника:

, где - число лишних связей, К – число замкнутых контуров, число шарниров, Со – число опорных связей.

2. Составляем рациональный вариант основной системы – это система, освобожденная от дополнительных связей. Такая система статически определима. Но вместо отброшенных связей необходимо ввести неизвестные силовые факторы.

Новая система будет называться эквивалентной. Важно, чтобы система оставалась статически неизменяемой.

3. Строим единичные эпюры от усилий Xi=1, совпадающих по направлению с неизвестными силовыми факторами, грузовую эпюру Мр.

4. Вычисляем коэффициенты канонического уравнения перемножением единичных эпюр: .

Вычисляем свободные члены канонического уравнения перемножением грузовых и единичных эпюр: .

5. Решаем систему канонических уравнений метода сил, получаем искомые неизвестные силовые факторы:

6. В исходной системе строим эпюру .

7. Строим эпюру , строим эпюру .

8. При необходимости производим проверки: деформационная для моментов и статическая для поперечных и продольных сил.

4. Сущность расчета статически неопределимых систем методом перемещений.

1. Определяем степень кинематической неопределимости системы по формуле:

, где ny – число углов поворота жестких узлов системы, nл – число независимых линейных перемещений рамы, связанных с изгибом ее элементов.

Строим основную систему метода перемещений, путем отбрасывания неизвестных перемещений: в жесткие узлы включаем плавающие заделки, фиксирующие углы поворота этих узлов; линейные смещения фиксируем соответствующими линейными связями.

3. Заменяем основную систему на эквивалентную, вводя вместо неизвестных силовых факторов единичные усилия Zi=1.

Строим единичные эпюры моментов от Zi=1, грузовую эпюру моментов Мр.

4. Вычисляем коэффициенты канонического уравнения перемножением единичных эпюр: .

Вычисляем свободные члены канонического уравнения перемножением грузовых и единичных эпюр: .

5. Решаем систему канонических уравнений метода перемещений, получаем искомые неизвестные силовые факторы:

6. В исходной системе строим эпюру .

7. Строим эпюру , строим эпюру .

8. Канонические уравнения являются уравнениями совместности перемещений исходной и основной систем по направлению отброшенных связей.

5. Понятие об определении частот и форм собственных колебаний.

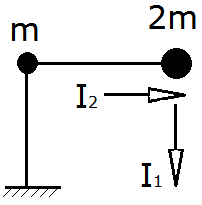n=2 (I1 и I2)

Частотное уравнение:

где m1=2m, m2=m+2m=3m, , i, j = 1, 2, причем Mi от Ii=1, , W – частота собственных колебаний системы.

Раскрывая определитель, получаем квадратное уравнение, корнями которого будут частоты W1 и W2, составляющие спектр частот, причем меньшая W будет называться частотой основного тона или опасной частотой собственных колебаний.

Форма колебаний определяется соотношением амплитудных перемещений присоединенных масс. Для определения формы колебаний используют канонические уравнения метода максимальных инерционных сил:

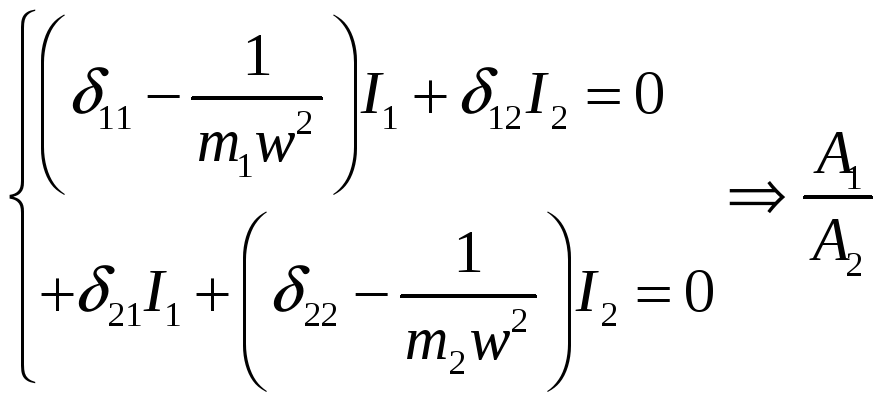(форма колебаний)

, где Ai – амплитуда i-й массы

6.1. Краткая характеристика методов расчета упругих систем на устойчивость: статический.

Ркр - ?

; (с – коэфф. жесткости пружины).

Рассматривается новая, иная форма равновесия. Для новой формы записываются уравнения равновесия статики, из которых определяются критические значения сжимающей нагрузки Ркр.

6.2. Краткая характеристика методов расчета упругих систем на устойчивость: энергетический.

А – работа внешних сил, П – потенциальная энергия.

При А≥П – система неустойчива, А<П – устойчива.

Возможные вариации:

при бЭ=0 – положение равновесия;

а) б2Э>0 – система устойчива;

б) б2Э=0 – система безразлична;

в) б2Э<0 – система неустойчива.

6.3. Краткая характеристика методов расчета упругих систем на устойчивость: динамический.

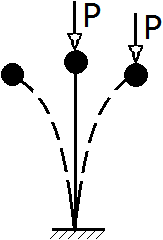
P<Pкр тогда W>0

P=Pкр тогда W0

7. Вид канонических уравнений метода перемещений при расчете рам на устойчивость.

Для отыскания критического состояния системы, исходное равновесие которой обозначено штриховыми линиями на рисунке соответствии с принципом малых возмущений задается отклонение некоторым малым воздействием (сила Т). Возмущенное состояние системы характеризуется искривлением первоначально прямых стержней и возникновением в общем случае поворотов и линейных смещений узлов. Эти линейные и угловые перемещения узлов принимаются за основные неизвестные в расчете на устойчивость методом перемещений.

Система канонических уравнений метода перемещений для расчета на устойчивость:

i = 1, 2,…, n.

или в развернутом виде:

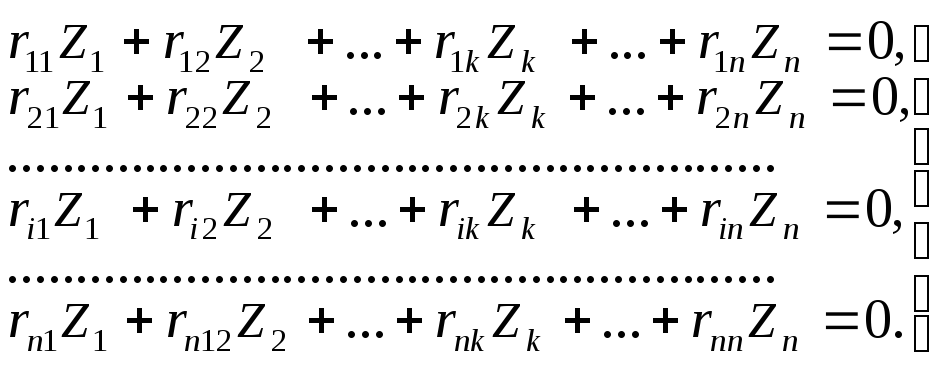
Матричная форма записи канонических уравнений:

где

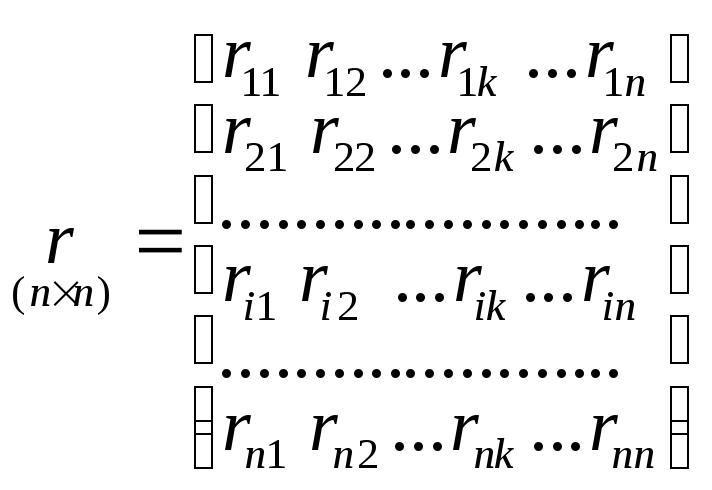- матрица внешней жесткости основной системы;

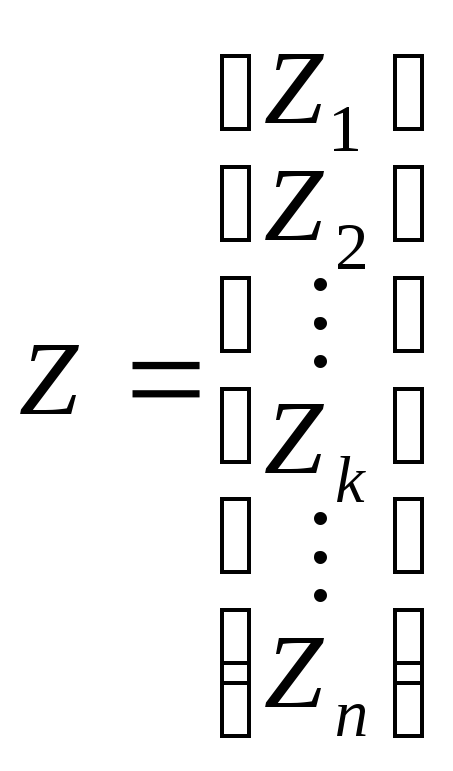- единичные перемещения.

Так как rik является функцией V, то рассчитав определитель матрицы (уравнение устойчивости), найдем Vкр. Таким образом можно найти Ркр:

.

Канонические уравнения описывают возмущенное состояние системы, качественно альтернативное исходному. Они линейны относительно основных неизвестных Z и однородны (не имеют свободных членов) – это следствие использования предпосылок линейной теории устойчивости.

Компоненты rik матрицы внешней жесткости представляют собой реакции введенных связей в единичных состояниях основной системы (от единичных смещений этих связей). Для определения rik можно использовать те же способы, что при расчетах на прочность.