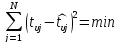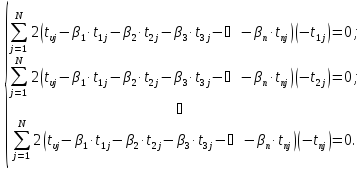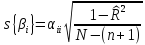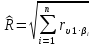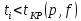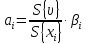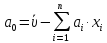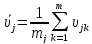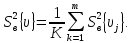Заочники 2013 ПланированиеЭкспер / Планирование эксперимента примеры / Методичка 3

Министерство образования и науки Российской Федерации

Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

«Магнитогорский Государственный Технический Университет

им. Г.И. Носова»

Методические указания для студентов специальности 002004 «Промышленная электроника» по теме

ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ УРАВНЕНИЯ РЕГРЕССИИ ПЕРВОГО ПОРЯДКА МЕТОДОМ МНОЖЕСТВЕННОГО РЕГРЕССИОННОГО АНАЛИЗА

курса «Планирование эксперимента»

Пишнограев Р.С.

Швидченко Д.В.

Суспицын Е.С.

Швидченко Н.В.

Магнитогорск

2009

Введение

Данные методические указания предназначены для проведения практических занятий со студентами третьего курса специальности «Промышленная электроника». Основным инструментом для проведения занятий является программный продукт Microsoft Excell. Это программное обеспечение позволяет обеспечить среднюю степень автоматизации процесса обучения, что с одной стороны даёт представление студентам о сути производимых ими действий, а с другой – избавляет от рутинных операций, связанных с арифметическими расчётами.

Структурно методические указания разделены на две части:

1. Краткие теоретические сведения, необходимые для выполнения практических занятий.

2. Задание на практическое занятие, с перечнем функций Microsoft Excell, необходимыми для его выполнения.

На практических занятиях студентам предлагается определить коэффициенты нелинейного двухфакторного уравнения регрессии методом множественного регрессионного анализа, выполнить проверку коэффициентов уравнения на значимость, оценить адекватность и работоспособность итогового уравнения регрессии, определить достоверность полученных результатов.

При разработке данных методических указаний предполагается, что студенты прослушали курс «Иноформатика» и имеют навыки работы в приложении Microsoft Excell. При этом некоторые расчётные выражения, используемые при выполнении практических заданий, всё же будут приведены в заключительной части указаний.

Для работы по данным методическим указаниям необходимо наличие авторской программы генерации текстовых файлов заданий (исходных данных). Кроме этого, для сокращения времени проверки правильности выполнения работ, удобно пользоваться авторской программой.

1. Теоретические сведения

Задачей множественного регрессионного анализа (МРА) является получение оценок коэффициентов множественного уравнения регрессии n-го порядка.

Схема эксперимента для данного случая представлена на рис. 1. На рисунке приняты следующие обозначения: 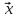– вектор входных переменных x_i; υ – функция цели; ε – случайные помехи; υ_н – наблюдаемая функция цели.

Рис. 1. Схема эксперимента по определению математического описания объекта

Предпосылками МКА являются следующие:

1. Случайные помехи ε(t) представляют собой стационарный случайный процесс с нормальным распределением, имеющим генеральные численные характеристики:

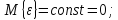
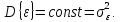
где M{ε} – математическое ожидание помех, D{ε} – генеральная дисперсия помех.

Помехи действуют аддитивно в течение всего эксперимента и независимо от входных величин x_i(t) (i = 1,2 … n).

2. Все случайные процессы x_i(t) стационарны и подчиняются нормальному закону распределения вероятности.

3. Искомая истинная регрессионная зависимость

полагается известной в виде линейного (первого порядка) уравнения. Другими словами, постулируется уравнения регрессии в виде

(1)

4. Все факторы x_i(t) линейно и функционально независимы друг от друга.

5. Все соседние измерения x_i,j(t), x_i,j+1(t) (j = 1, 2, …, N) по любому фактору x_i(t) корреляционно независимы.

6. Погрешность δx_i измерения любого фактора x_i(t) значительно меньше погрешности δυ измерения функции отклика. А погрешность δυ измерения функции отклика, в свою очередь, мала по сравнению с величиной помех ε.

7. В уравнение регрессии (1) включены все значимые факторы x_i(t), существенно влияющие на значение функции цели υ.

Допустим, все предпосылки выполнены, собрано достаточное количество экспериментальных данных с учётом эквивалентного запаздывания объекта, и экспериментальные данные сгруппированы в табл. 1.

Табл. 1. Исходные экспериментальные данные

j	x1	x2	x3	…	xn	υн
1	x11	x21	x31	…	xn1	υн1
2	x12	x22	x32	…	xn2	υн2
…	…	…	…	…	…	…
N	x1N	x2N	x3N	…	xnN	υнN

На начальном этапе определения уравнения регрессии выполняют расчёт точечных оценок входных параметров и функции отклика по выражениям:

Затем выполняют нормирование всех параметров по выражениям:

(2)

Величины t, полученные в результате нормирования по выражениям (2) обладают следующими свойствами:

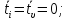
Таким образом, все входящие в эксперимент параметры становятся равновеликими и изменяются в равных пределах. Графически результат операции нормирования для случая двух входных переменных представлен на рис. 2. Нормирование заключается в переносе начала координат из точки (0;0) в точку (пунктирная стрелка рис. 2, а) и масштабировании осей по размерам K₁ и К₂.

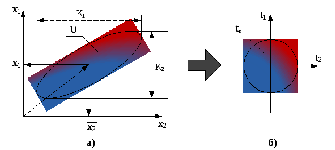Рис. 2. Графическая интерпретация операции нормирования для случая двух входных параметров

В нормированных величинах изменение функции отклика определяется долей влияния каждого параметра, т.е. коэффициентом уравнения регрессии. После выполнения операции нормирования табл. 1 преобразуется в форму табл. 2,

Табл. 2. Нормированные экспериментальные данные

j	t1	t2	t3	…	tn	tυ
1	t11	t21	t31	…	tn1	tυ1
2	t12	t22	t32	…	tn2	tυ2
3	t13	t23	t33	…	tn3	tυ3
…	…	…	…	…	…	…
N	t1N	t2N	t3N	…	tnN	tυN

а уравнение регрессии (1) находится в виде:

,

(3)

где 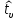– предсказанное (расчётное) нормированное значение функции цели;

β_i – коэффициенты нормированного уравнения регрессии (3), определяющие степень влияния входных параметров x_i(t) на функцию цели υ.

Важным свойством коэффициентов β_i нормированного уравнения регрессии (3) является то, что по ним можно оценить значимость каждого входного параметра. В случае если параметр не оказывает значимого влияния на функцию цели, его можно исключить из уравнения регрессии.

Следует отметить, что в нормированном уравнении регрессии (3) отсутствует свободный член β₀. Это связано с тем, что в результате нормирования было выполнено центрирование всего эксперимента (перенос точки начала координат).

Поиск коэффициентов β_i осуществляется методом наименьших квадратов, т.е. из условия

(4)

Для расчёта коэффициентов β_i, удовлетворяющих условию (4) находят частные производные левой части уравнения (4) по каждому из параметров β_i и приравнивают их к нулю. В результате получают систему из n уравнений с n неизвестными:

(5)

После раскрытия скобок и упрощения система уравнений (5) примет вид:

(6)

Если в системе уравнений (6) каждое уравнение разделить на величину (N–1), то, с учётом (2), система (6) может быть преобразована к виду

(7)

где

	(8)
	(9)

Выражение (8) есть ни что иное как формула расчёта коэффициентов корреляции между входными параметрами x_l(t) и x_k(t), а выражение (9) – формула расчёта коэффициента корреляции между входным параметром x_k(t) и функцией цели υ(t).

С переходом к матричной записи системы уравнений (7) и с учётом того, при l = k, получим

(10)

где

Отсюда

(11)

где K^-1 – матрица, обратная корреляционной матрице K.

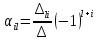(Δ – главный определитель матрицы K n-го порядка; Δ_il­ – минор главного определителя Δ, получаемый путём вычёркивания l-ой строки и i-го столбца из прямой матрицы K).

После определения численных значений коэффициентов β_i нормированного уравнения регрессии (3), выполняют их оценку на значимость. При этом пользуются критерием Стьюдента, проверяя гипотезу о равенстве математического ожидания коэффициента β_i нулю.

Для этого формируют эмпирическое значение t-статистики по выражению

(12)

В выражении (12) значение M{ β_i } принимают равным нулю, а величину s{ β_i } находят по формуле

(13)

Здесь

(14)

– оценка множественного коэффициента корреляции.

Критическое значение t_КР t-статистики Стьюдента выбирают исходя из необходимой вероятности p и числа степеней свободы f = N – (n + 1).

При выполнении условия

(15)

делают вывод о том, что коэффициент β_i не значимо отличается от нуля и данным слагаемым в уравнении регрессии можно пренебречь. Однако после отбрасывания незначимого коэффициента β_i необходимо выполнить решение системы уравнений (7) заново для оставшихся (n – 1) параметров.

После окончательного определения коэффициентов β_i осуществляется обратный переход к ненормированному уравнению регрессии. Это делают путём расчёта коэффициентов 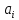по выражениям:

	(16)
	(17)

Работоспособность полученного уравнения регрессии определяется по значению множественного коэффициента корреляции 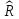. В [3] показано, что уравнение регрессии имеет хорошую работоспособность, если выполняется условие:

Если оценка 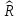окажется меньше 0,8, причинами этого могут быть:

1. в уравнение регрессии не включены ещё какие-то значимые факторы, существенно влияющие на функцию цели;

2. регрессионная зависимость 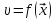должна быть описана полиномом более высокого порядка;

3. базовая точка в проведённом эксперименте находится вблизи главного экстремума целевой функции.

В первом случае исследователю необходимо более детально изучить объект исследования и учесть все значимые факторы в уравнении регрессии. Во втором случае необходимо постулировать иной вид уравнении регрессии и определить его коэффициенты методом множественного регрессионного анализа. В третьем случае необходимо расширить диапазон изменения входных переменных и также перейти к уравнению регрессии более высокого порядка.

Адекватность уравнения регрессии проверяется в том случае, когда для каждой комбинации входных параметров x_i(t) выполнено m измерений функции цели υ. В этом случае для определения коэффициентов уравнения регрессии по приведённой методике m параллельных измерений заменяют их средним значением:

(18)

Для проверки адекватности уравнения регрессии выполняют расчёт дисперсии воспроизводимости, характеризующую влияние случайного шума на функцию цели при прочих одинаковых условиях,

(19)

и остаточную дисперсию, характеризующую насколько неидеально уравнение регрессии описывает объект исследования

(20)

где d ­– число членов уравнения регрессии после отбрасывания незначимых оценок коэффициентов .

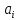Если имеется возможность провести параллельные опыты в K точках факторного пространства, то для анализа адекватности уравнения регрессии берут усреднённое значение дисперсии воспроизводимости:

(21)

Если число параллельных опытов в каждой точке факторного пространства было неодинаковым, то для расчёта дисперсии воспроизводимости используют усложнённую формулу расчёта, учитывающую «вес» каждой j-ой оценки дисперсии:

(21)

где ν_j – относительная частота, определяемая как

(22)

После расчёта величин 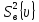и формируют эмпирическое значение F-статистики Фишера:

(23)

и сравнивают его с критическим значением, выбранным для необходимого уровня значимости q = 1 – p, числа степеней свободы числителя f_ЧИСЛ = f_ОСТ = N – d и числа степеней свободы знаменателя f_ЗНАМ = f_В = 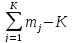. Если выполняется условие

(24)

то делается вывод об адекватности уравнения регрессии.

2. Задание на практические занятия

Выполнение практических занятий по приведённому материалу осуществляется в компьютерном классе при помощи приложения MS Excell. Данное приложение предлагает средний уровень автоматизации расчётов, что позволяет свести к минимуму рутинные расчётные операции, обеспечивая при этом ручное выполнение основных операций.

На практические занятия каждому студенту выдаётся два текстовых файла с исходными данными эксперимента: №вар_mra.txt и №вар_lin_mra.txt. Формат файлов приведён в табл. 3, 4. Схема эксперимента приведена на рис. 3.

Рис. 3. Схема эксперимента для практических занятий

На рис. 3 приняты следующие обозначения: X₁, X₂ – входные параметры, V – функция цели, ε – случайные помехи.

В качестве задания студентам предлагается определить коэффициенты полного уравнения регрессии второго порядка:

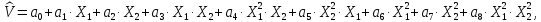
выполнить проверку их значимости, проверить полученное уравнение регрессии на работоспособность и адекватность.

После выполнения работы студенты должны составить отчёт о результатах анализа.

При выполнении работы целесообразно использовать следующие встроенные функции приложения MS Excell:

СРЗНАЧ(массив)	– расчёт среднего значения элементов массива;
КОРРЕЛ(массив1; массив2)	– расчёт коэффициента корреляции между двумя массивами данных;
ДИСП(массив)	– расчёт дисперсии элементов массива;
СТЬЮДРАСПОБР(p; f)	– расчёт квантиля распределения Стьюдента для заданной вероятности p и числа степеней свободы f;
FРАСПОБР(p; fЧИСЛ; fЗНАМ)	– расчёт квантиля распределения Фишера для заданной вероятности p, числа степеней свободы числителя fЧИСЛ и , числа степеней свободы знаменателя fЗНАМ;
СЧЁТ(область)	– определение количества заполненных ячеек в указанной области.
СУММПРОИЗВ(массив1; массив2)	– расчет суммы произведений элементов двух массивов данных.

Табл. 3. Формат файла №вар_mka.txt

		X1
		X11		X12		…	X1i		…	X1n
X2	X21	V111 V112 … V11k … V11m	V211 V212 … V21k … V21m		…		Vi11 Vi12 … Vi1k … Vi1m	…		Vn11 Vn12 … Vn1k … Vn1m
	X22	V121 V122 … V12k … V12m	V221 V222 … V22k … V22m		…		Vi21 Vi22 … Vi2k … Vi2m	…		Vn21 Vn22 … Vn2k … Vn2m
	…	…	…		…		…	…		…
	X2j	V1j1 V1j2 … V1jk … V1jm	V2j1 V2j2 … V2jk … V2jm		…		Vij1 Vij2 … Vijk … Vijm	…		Vnj1 Vnj2 … Vnjk … Vnjm
	…	…	…		…		…	…		…
	X2h	V1h1 V1h2 … V1hk … V1hm	V2h1 V2h2 … V2hk … V2hm		…		Vih1 Vih2 … Vihk … Vihm	…		Vnh1 Vnh2 … Vnhk … Vnhm
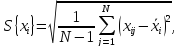
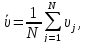
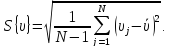
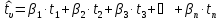