Повторение испытаний
Если производится несколько испытаний, причем
вероятность события А в каждом испытании не зависит от исходов других испытаний , то такие
испытания называют независимыми относительно
события А.
Будем предполагать далее, что Р(А) = р, т.е. вероятность р всегда одинакова (0 < р < 1), и
поставим задачу вычислить вероятность того, что
при n испытаниях событие А осуществится ровно k раз. Ответ на этот вопрос дает формула
Бернулли.
Вероятность того, что в n независимых испытаниях ( в
каждом из которых вероятность Р(А) = р одинакова ) событие А наступит ровно k раз ( в любой
последовательности), равна
Pn (k) Cnk pk qn k
, где
q 1 p,Ck n(n 1)....(n k 1) , k! 1 2 3 ... k
n k!
В частности,
Cn0 1,Cn1 n,Cnk Cnn k
Пример
Два равносильных шахматиста играют в шахматы. Что вероятнее: выиграть 3 партии из 6 или 4 партии из 8 ? (ничьи во внимание не принимаются).
Играют два равносильных шахматиста, поэтому вероятность выигрыша в одной партии равна ½. Следовательно , вероятность проигрыша q = ½ .
Вероятность р одинакова. Последовательность выигрыша не играет роли. Значит, применим формулу Бернулли.
Вероятность того, что будут выиграны 3 партии из 6 :
P (3) |
C |
3 |
3 |
q |
3 |
|
6 5 4 |
1 |
3 |
|
1 3 |
|
20 |
|
||
6 |
p |
|
|
|
|
|
|
|
|
|
|
|||||
6 |
|
|
|
|
|
1 2 3 |
|
2 |
|
2 |
|
64 |
|
|||
Вероятность |
|
|
|
|
|
|
|
|
|
|
|
8: |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
P (4) |
|
4 |
4 |
|
4 |
|
8 7 6 5 |
1 |
4 |
|
1 |
4 |
70 |
|
35 |
||
C |
|
p |
q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
8 |
8 |
|
|
|
|
1 2 3 4 |
|
2 |
|
2 |
|
256 |
128 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Нетрудно видеть, что
P6 (3) 6420 12840 P8 (4) 12835
Вероятность того, что в n испытаниях
I) Событие А наступит менее k раз
PI Pn (0) Pn (1) ... Pn (k 1)
II) Событие А наступит не более k раз
PII Pn (0) Pn (1) ... Pn (k)
III) Событие А наступит более k раз
PIII Pn (k 1) Pn (k 2) ... Pn (n)
IV) Событие А наступит не менее k раз
PIV Pn (k) Pn (k 1) ... Pn (n)
Нетрудно видеть, что |
|
|
|
|
|||
PIV 1 PI , |
|
PIII 1 PII |
k1 |
k2 |
|||
|
|
|
|
|
|
||
V) Событие А наступит не менее и не более |
|||||||
P P |
n |
(0) P |
n |
(1) ... P |
n |
(k 1) |
k2 k1 |
I |
|
|
|
|
|||
Пример
Монету бросают 5 раз. Найти вероятность того, что «герб» выпадет :
а) менее 2-х раз б) не менее 2-х раз
Вероятность того, что в каждом испытании выпадет «герб» р |
||||||||||||||||||||||||||
a) |
= ½ , q = 1-p = ½ , n=5 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
Pa |
P5 (0) P5 (1) |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
0 |
|
1 |
0 |
|
1 |
|
5 |
|
|
|
1 |
|
1 |
|
|||||
|
|
P (0) C |
5 |
|
|
|
|
|
1 1 |
|
|
|
|
|
||||||||||||
|
|
|
|
|
||||||||||||||||||||||
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
32 |
|
32 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
||||||
|
|
P (1) C |
1 |
|
1 1 |
|
1 |
4 |
|
|
5 |
|
|
|
|
|
|
|||||||||
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
5 |
|
|
|
|
|
|
|
|
|
32 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
||||||
|
|
P |
1 |
|
5 |
|
|
6 |
|
|
3 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
б) |
a |
32 |
|
|
|
32 |
|
32 |
|
16 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Pb 1 Pa 1 163 1613
Случайные величины – величины , которые
принимают те или иные значения.
Дискретные случайные величины
Определение: Дискретной называют случайную величину , возможные значения которой есть
отдельные изолированные числа, причем величина
принимает эти значения с определенными
вероятностями.
Возможные значения дискретной случайной величины можно пронумеровать.
Определение: Законом распределения дискретной случайной величины называют перечень ее возможных значений и соответствующих им вероятностей.
Способы задания закона 
распределения
случайной величины
1) |
Табличный |
X |
x1 |
x2 ... |
xn |
|
|
|
|
|
n |
p |
p1 |
p2 ... |
pn |
|
|
|
|
|
p2 |
... pn |
1 |
|
|
|
|
Здесь |
pi p1 |
|
|
||||
|
|
i 1 |
|
|
|
P( X x ) (x ) |
||
2) |
|
|
|
|
|
|||
Аналитический, т.е. в виде формулы |
i |
i |
||||||
или с помощью функции распределения. |
|
|
||||||
3) |
Графический |
|
|
|
|
|
|
|
|
В прямоугольной системе координат строят точки |
|
||||||
M1 (x1; p1 ), M 2 |
|
отрезками прямых. |
Полученную |
|
||||
(x2 ; p2 ),..., M n (xn ; pn ) |
|
|
распределения |
|||||
|
|
|
многоугольником |
|||||
Биномиальным называют закон распределения
дискретной случайной величины Х – числа появления события в n независимых испытаниях, в
каждом из которых вероятность появления
события равна р.
Вероятность возможного значения X = k вычисляется
по формуле P (k) Ck pk qn k |
|
n |
n |
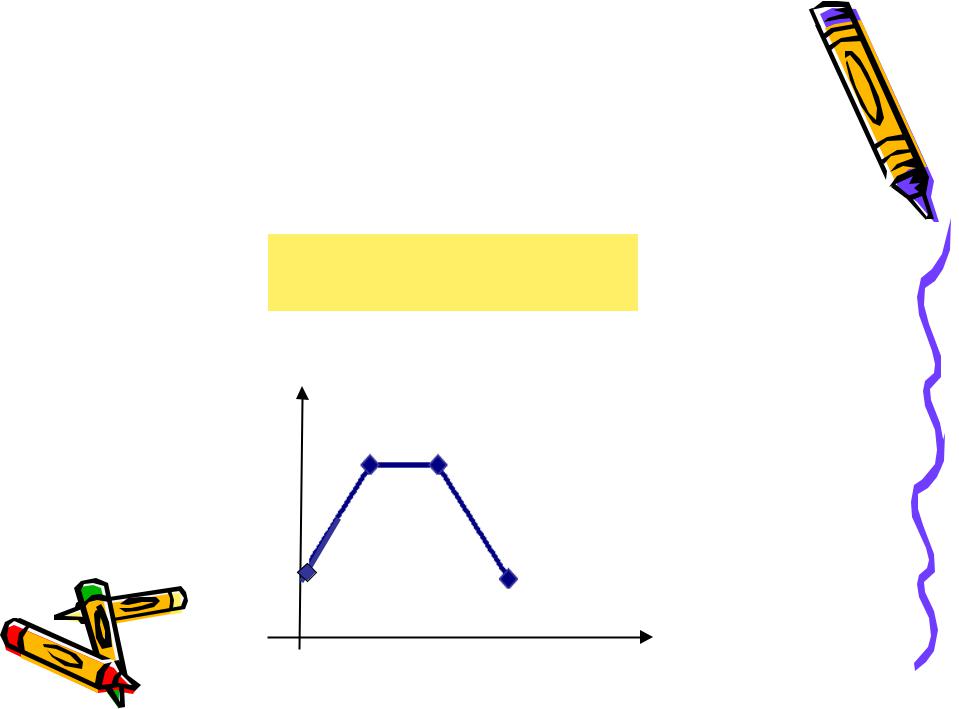
Пример: n = 3, p = q = ½ . Построить многоугольник распределения.
3
2 |
|
|
|
1 |
1 |
2 |
3 |
0 |
Закон Пуассона
Если число испытаний n велико, а вероятность р
появления события в каждом испытании очень мала ( р
≤ 0,1) , то используют приближенную формулу:
P (k) k e |
|
|
n |
k! |
, |
|
||
где k – число появлений события в n независимых
испытаниях,np
- (среднее число появлений события в испытаниях).
Говорят тогда, что случайная величина распределена по
закону Пуассона
Пример
Написать биномиальный закон распределения дискретной случайной величины Х – числа появлений «герба» при 2-х
бросаниях монеты
n=2, p = ½ ; q = ½ ; X = 0 ; 1 ; 2.
P (0) |
C |
0 |
|
1 |
0 |
|
1 |
2 |
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|||
2 |
|
|
|
|
2 |
|
|
4 |
|||
|
|
|
|
2 |
|
|
|
|
|
||
P (1) C1 |
1 |
1 |
2 1 |
1 |
|||||||
2 |
2 |
2 |
2 |
|
|
|
4 |
|
2 |
||
P (2) |
C |
2 |
|
1 |
2 |
|
1 |
0 |
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|||
2 |
|
|
|
|
2 |
|
|
4 |
|||
|
|
|
|
2 |
|
|
|
|
|
||
|
|
|
|
|
|
X |
|
|
|
0 |
1 |
|
|
|
|
|
|
P |
|
|
1/4 |
1/2 |
|
Итак,
2 Проверка условия pi 1:
1/4 |
1 |
|
1 |
|
1 |
1 1 1 |
|
|
|
||||
|
4 |
|
2 |
|
4 |
|