
Презентации по математике / Презентации / 09.Дифференциальное исчисление
..ppt
I.ПРОИЗВОДНАЯ ФУНКЦИИ. ОПРЕДЕЛЕНИЕ. ГЕОМЕТРИЧЕСКИЙ И ФИЗИЧЕСКИЙ СМЫСЛ.
II. ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ
III.ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ. ТАБЛИЦА ПРОИЗВОДНЫХ
ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ.
IV.ПРИМЕРЫ

|
I. |
ОПРЕДЕЛЕНИЕ |
|
|
|
|
|
ПУСТЬ |
х – ПРИРАЩЕНИЕ |
х – |
|
|
|
АРГУМЕНТА х. ТОГДА х+ |
|||
|
|
НОВОЕ ЗНАЧЕНИЕ АРГУМЕНТА, А |
|||
|
|
f(х) = f(х+ х) – f(x) |
|
||
|
|
-СООТВЕТСТВУЮЩЕЕ |
|
|
|
|
|
ПРИРАЩЕНИЕ ФУНКЦИИ f(х). |
|||
|
|
|
|
f(х) |
|
|
СОСТАВИМ ОТНОШЕНИЕ |
Х . |
|
||
|
ПО АНАЛОГИИ С ДВИЖЕНИЕМ В |
||||
|
|
ФИЗИКЕ ЭТО ОТНОШЕНИЕ |
|
||
|
|
МОЖНО НАЗВАТЬ СРЕДНЕЙ |
|||
|
|
СКОРОСТЬЮ ИЗМЕНЕНИЯ |
|
||
Пусть х O, ТОГДА ПРЕДЕЛ |
ФУНКЦИИ. |
|
|
||
|
|
|
|
||
НАЗЫВАЕТСЯ ПРОИЗВОДНОЙ ФУНКЦИИ f(x) В ТОЧКЕ Х. |
|
|
|||
ДРУГИЕ ОБОЗНАЧЕНИЯ: Y’ |
, |
. |
|
|
|

ЕСЛИ УКАЗАННЫЙ ПРЕДЕЛ СУЩЕСТВУЕТ, ТО ФУНКЦИЯ f(x) НАЗЫВАЕТСЯ
ДИФФЕРЕНЦИРУЕМОЙ В ДАННОЙ ТОЧКЕ х. ЕСЛИ ЖЕ ПРЕДЕЛ
РАВЕН ∞, ТО ГОВОРЯТ, ЧТО ФУНКИЯ f(x) ИМЕЕТ БЕСКОНЕЧНУЮ ПРОИЗВОДНУЮ.
ДОКАЖЕМ, ЧТО Х’=1.
В ЭТОМ СЛУЧАЕ f(x) = X, f(x+ x) = x+ x. ПРИРАЩЕНИЕ ФУНКЦИИ f(x) = f(x+ x) – f(x) = X+ X - X =
|
X |
СОСТАВИМ ОТНОШЕНИЕ |
|
F(x) |
X |
X |
X |
X’ = lim 1 = 1 X’ = 1 , ЧТО И ТРЕБОВАЛОСЬ |
|
ДОКАЗАТЬ. |
|

|
ГДЕ |
|
- УГОЛ НАКЛОНА КАСАТЕЛЬНОЙ М0N (ПРОВЕДЕННОЙ К |
||
КРИВОЙ f(x) В ТОЧКЕ Х) К ПОЛОЖИТЕЛЬНОМУ |
|
|
НАПРАВЛЕНИЮ ОСИ Оx. ЧТО ТАКОЕ КАСАТЕЛ |
? ЕСЛИ |
|
ПРИ |
(М1 М0) СЕКУЩАЯ М1М0 СТРЕМИТСЯ ЗАНЯТЬ |
|
ПОЛОЖЕНИЕ ПРЯМОЙ М0N, ТО ЭТА ПРЯМАЯ М0N |
|
|
НАЗЫВАЕТСЯ КАСАТЕЛЬНОЙ К КРИВОЙ f(x) В ТОЧКЕ М0 |
||
(ПРИ |
|
|
ПУСТЬ ТЕЛО ДВИЖЕТСЯ ПРЯМОЛИНЕЙНО, И ЗАКОН ЕГО |
|
|
ДВИЖЕНИЯ ПО ВРЕМЕНИ ЗАДАН УРАВНЕНИЕМ S=S(t), ГДЕ S- |
||
РАССТОЯНИЕ, ПРОЙДЕННОЕ К МОМЕНТУ ВРЕМЕНИ t. ТОГДА |
||
ПРОИЗВОДНАЯ S’(t) ЕСТЬ МНГНОВЕННАЯ СКОРОСТЬ В МОМЕНТ t, |
||
Т.Е. |
|
|

ПУСТЬ U’ И V’ СУЩЕСТВУЮТ, Т.Е. ФУНКЦИИ U(x) И |
|
V(x) |
|
ДИФФЕРЕНЦИРУЕМЫ, ТОГДА |
|
1.( U + V )’ = U’ + V’ |
|
2.( UV )’ = U’ V + V’ U – ФОРМУЛА |
|
ЛЕЙБНИЦА |
|
3. ( )’ = |
, V ≠ 0 |
4.( CU )’ = C U‘ , C – const. |
|

Пусть y = f(u), ГДЕ u = u(x), Т.Е. y = f(u(x)) – СЛОЖНАЯ ФУНКЦИЯ, ПРИЧЕМ ФУНКЦИИ f(u) И u(x)
ДИФФЕРЕНЦИРУЕМЫ. ТОГДА ПРОИЗВОДНАЯ y’(x) МОЖЕТ БЫТЬ НАЙДЕНА ПО ФОРМУЛЕ:
Y’(x) = f’u(u(x)) . u’(x).
В ЧАСТНОСТИ, ЕСЛИ f(u) – ЭЛЕМЕНТАРНАЯ ФУНКЦИЯ, ТО
ПОЛУЧАЕМ ТАБЛИЦУ ПРОИЗВОДНЫХ ОСНОВНЫХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ:1. С ’= 0, C – const.
2. (Un)’= n . Un-1 . U’ , n - const. 3. ( )’ = -
)’ = - 
 . U’
. U’
4. ( U)’ = 
 . U’
. U’
5. (sinU)’ = cosU . U’
7.(tgU)’ =


 . U’
. U’
8.(ctgU)’ = - 


 . U’
. U’
9.(arcsinU)’ =  . U’
. U’
10.(arccosU)’ =  . U’
. U’
11.(arctgU)’ =
 . U’
. U’
12.(arcctgU)’ = -



 . U’
. U’
13.(аu)’ = аu . lna . U’ , a>O, a≠1
14.(еu)’ = еu 
15. |
(log U)’ = |
. U’, a>O, a≠1 |
|
a |
|
16. |
(lnU)’ = . U’ |
|
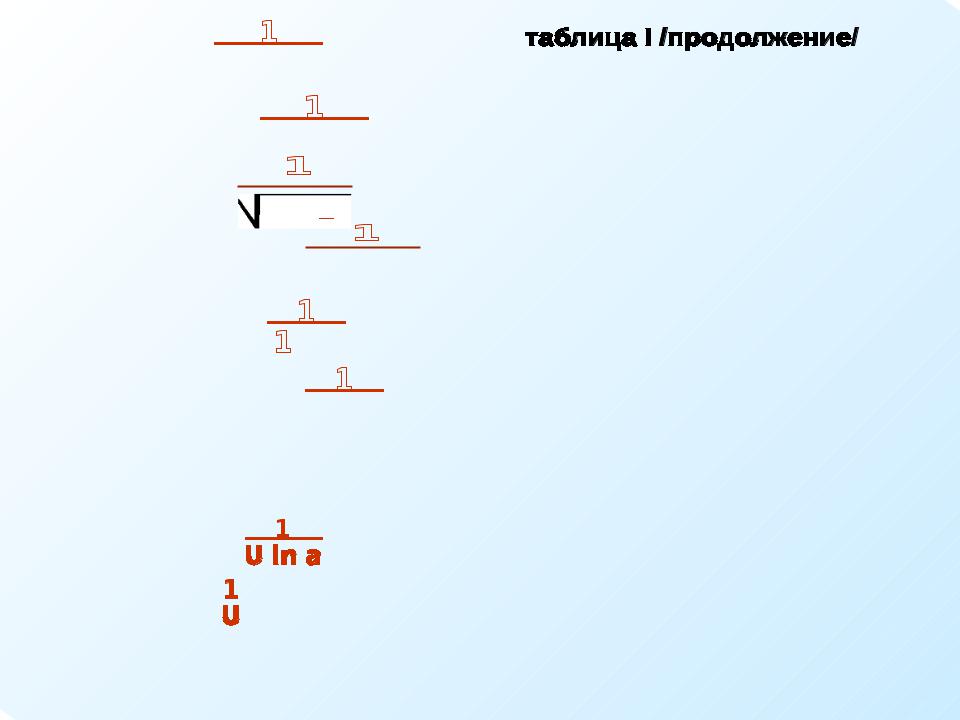
ЗАМЕЧАНИЕ: ЕСЛИ U = Х, ТО U’= X’=1,a ТАБЛИЦА I

1.C’ = 0, C – const.
2.(Xn)’ = nXn-1 , n – const.
3.( )’= -
)’= - 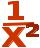
4.( X)’=

5.(sinX)’ = cosX
6.(cosX)’ = - sinX
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.

1. y = X2 -5X + 4 , y - ?
y’=(X2 – 5X + 4)’= (X2)’– (5X)’+ 4’= 2X – 5.X’ + 0 = 2X-
5.1= = 2X – 5.
2. y= 4 X + - , y’ = ?
ПРЕДВАРИТЕЛЬНО ПРЕОБРАЗУЕМ у К СУММЕ СТЕПЕННЫХ
ФУНКЦИЙ, ВВОДЯ ДРОБНЫЕ И ОТРИЦАТЕЛЬНЫЕ ПОКАЗАТЕЛИ 

y= X1/4 + 5X-1/3 - |
X-3. |
ТЕПЕРЬ y’= X-3/4 + 5(- )X-4/3 – |
- (-3)X-4 = |
- |
+ |
3. y = X5(2-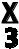 +3X2) ,
+3X2) ,  - ?
- ?
1-Й СПОСОБ (ФОРМУЛА ЛЕЙБНИЦА).
y’ = (X5)’.(2- + 3X2)+(2- +3X2)’.X5 =

2-Й СПОСОБ. ВНАЧАЛЕ РАСКРОЕМ СКОБКИ. y = X5(2-  +3X2) = (2X5 -
+3X2) = (2X5 - 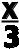 + 3X7 ). ТЕПЕРЬ
+ 3X7 ). ТЕПЕРЬ
y’ = (2X5 - +3X7)’ = (2X5)’ –
+3X7)’ = (2X5)’ – 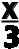 ) + (3X7)’ =
) + (3X7)’ =
= 10X4 – 2X5 + 21X6.
+ 21X6.
4. f(x) = 



 , f’(x) - ?
, f’(x) - ?
f’(x) = (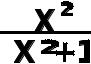 )’=
)’=
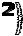

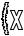
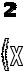




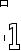

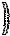







=
5. y = 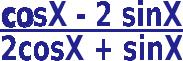







 y’ = ?
y’ = ?
y’=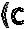

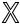

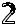
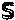


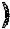


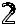
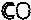
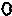


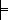




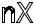


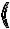




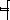
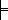








 =
= 




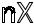

=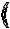










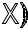



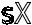

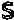


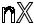







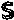




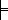


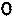




 =
=


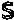


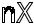
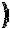
=







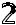












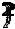 =
=
