Основы_акустики_Гринченко_Вовк

где vm = mπ/a, m=0,1,2,… В частности для нормальной производной на поверхности цилиндра имеем

(9.142)

Функцию p2 будем искать в виде суперпозиции цилиндрических волн, уходящих от клина,

этом для нормальной производной на поверхности цилиндра имеем

Неизвестные коэффициенты Cm определим из условия (9.139), кото- рое, с учетом (9.142) и (9.144), приводит к уравнению

9.13. Принцип взаимности

Принцип взаимности или теорема взаимности постулиру-

ет для линейных систем связь между двумя источниками и создавае- мыми ими полями в местах расположения источников. Эта связь оп- ределяется простым соотношением p21 = p12Q2 /Q1, где Q1 - объем-

ная колебательная скорость источника в некоторой точке x1 , а p12 - давление, создаваемое источником Q1 в точке x2 ; Q2 - объемная ко- лебательная скорость источника в точке x2 , а p21 - давление, созда- ваемое источником Q2 в точке x1 . Хотя данное соотношение вполне

очевидно, тем не менее, приведем формальное доказательство его справедливости на основе использования функции Грина.

Функция Грина свободного пространства обладает свойством G(r,r0) = G(r0,r), поскольку ее зависимость от координат векторов r и r0 определяется через модуль их разности, т.е. G(r,r0) = G( r – r0 ) (см.

формулу (9.29)). Как оказывается, соотношение

имеет общий характер в акустике и является, по сути, математиче- ской формулировкой принципа взаимности. Впервые на существова- ние принципа взаимности в акустике указал Гельмгольц, а несколько позднее Рэлей [50] обобщил эти сведения и получил обобщенный принцип взаимности, который связывает различные типы внешних воздействий на линейную динамическую систему с эффектами этих влияний.

Например, покажем, что формула (9.148) справедлива в случае наличия в пространстве тел, поверхности которых являются либо идеальными (т.е. акустически жесткими или акустически мягкими), или импедансными (см. параграф 5.7).

592

Рассмотрим поле в некоторой точке r среды, которое создается то- чечным источником, расположенным в точке r0: G(r,r0). Это поле, оче- видно, удовлетворяет неоднородному уравнению

Аналогично вводим в рассмотрение поле, которое создается в той же точке точечным источником, расположенным в точке r1: G(r,r1), поле удовлетворяет уравнению

Умножаем (9.149) на G(r,r1), а (9.150) на G(r,r0) и вычитаем второе со- отношение из первого, в результате получаем

Проинтегрируем равенство (9.151) по объему, ограниченному поверх- ностью тел S, бесконечно удаленной поверхностью Σ и разрезами L

(рис. 9.21). С помощью формулы Грина (9.33) сведем интегрирование по объему к интегрированию по указанной окружающей поверхно- сти. Учитывая свойство интегралов от дельта-функций (9.15), получа- ем

Интеграл по поверхности Σ в (9.152) равен нулю вследствие условия излучения, а интегралы вдоль берегов разреза L равны нулю из-за противоположного направления нормалей к ним. Интегралы по по- верхности тела S также превращаются в нуль вследствие указан- ных выше граничных условий.

Рис. 9.21. Пример определения принципа взаимности

593

Итак, справедливость равенства (9.148) доказана. Это соотноше- ние означает, что если точечный источник, расположенный в точке r0, создает некоторое давление в точке r1, то при перемещении его в точку r1 он будет создавать такое же давление в точке r0.

Принцип взаимности используется при построении решения аку- стических задач, если такое изменение в расположении источника и точки наблюдения упрощает практические расчеты. Особое значение он имеет при использовании соответствующих методов измерения акустических величин (см. раздел 13).

9.14. Вычисление звуковых полей плоских излучателей с помощью интеграла Фурье

Формулы (9.68), которые дают возможность рассчитать звуковое поле плоского излучателя, получены на основе интеграла Кирхгоффа. Но для этой цели можно применить другой способ, кото- рый базируется на интегральном преобразовании Фурье. С целью уп- рощения выкладок рассмотрим двумерный случай.

В параграфе 5.10 была рассмотрена процедура определения в пространстве бегущей волны согласно заданному на некоторой плос- кости распределению давления или колебательной скорости. Исполь- зуем этот прием для решения поставленной задачи. Сначала вспом- ним, как это делается.

Рис. 9.22. Пример применения преобразования Фурье

Пусть на плоскости z = 0 имеем распределение колебательной ско- рости, которое представляет собой бегущую волну вдоль направления оси Ox (рис. 9.22) (временной множитель exp(–iωt) опускаем):

где β — постоянная распространения волны. В таком случае давление в полупространстве z > 0 имеет вид

594

Вернемся к формуле (9.158). Запишем ее иначе, воспользовавшись заменой

(9.160) не должна изменить характер представления звукового поля, т.е. должны сохраниться в наличии все эти волны. Этого можно дос- тичь, если выполнить интегрирование в комплексной области по пе- ременной α = Re α + iImα. Итак, формула (9.158) будет иметь вид

где Г — контур интегрирования (рис. 9.23).

Рекомендуем читателю самостоятельно, расписывая соотношение sinα и cosα, где α = Reα + iImα, убедиться в том, что участок контура Г на оси абсцисс (от –π/2 к π/2) соответствует однородным плоским волнам, которые распространяются в полупространстве z > 0 под уг- лом α к оси Oz. Эти волны характеризуются волновым вектором k = {k sinα, k cosα}. Наоборот, участки контура Г, параллельные оси ординат, определяют неоднородные волны. Эти волны распростра- няются вдоль оси Ох с постоянной распространения kch(Imα), а вдоль оси Oz их амплитуда уменьшается по экспоненциальному закону exp(–kzsh(Imα)), z ≥ 0. Причем левая ветвь контура Г соответствует неоднородным волнам, которые распространяются в отрицательном направлении оси Ох, а правая — в положительном направлении.

Рис. 9.23. Контур интегрирования Г

Вводя полярные координаты r, θ с центром в точке O (рис. 9.22), получим соотношение между декартовыми и полярными координата- ми: x = r sinθ, z = r cosθ, с учетом которых выражение (9.161) будет иметь вид

596

Итак, формула (9.161) или (9.162) определяет поле давления в по- лупространстве z > 0, представляющее собой суперпозицию однород- ных и неоднородных волн. Если нас интересует дальнее поле, то по- нятно, что достаточно учитывать только однородные волны. В таком случае формула (9.162) упростится, ведь интегрирование нужно вы- полнять только по действительному параметру α на интервале от –π/2

к π/2, т.е.

−π2

Например, рассмотрим дальнее поле излучателя с распределением колебательной скорости:

т.е. имеем одинаковую амплитуду колебательной скорости на полосе шириной 2а (рис. 9.22). Согласно преобразованию (9.157) определим спектральную функцию V(β), которая характеризует амплитуду бегу- щих плоских волн. Подставляя (9.164) в (9.157), получаем

Подставляя (9.166) в (9.163), получаем выражение для дальнего поля плоского излучателя с распределением колебательной скорости

(9.164):

Поразмышляем над формулой (9.167). Для дальнего поля величина волнового расстояния до точки наблюдения kr >> 1, кроме того, r >> a (r, θ — координаты точки наблюдения). Подынтегральная функция интеграла (9.167) является произведением двух функций. Первая из

но медленно, а вторая exp(ikr cos(θ – α)) за счет большого числа kr бы- стро осциллирует. Это приводит к тому, что интегралы такого типа даже при наличии современных ЭВМ вычислить практически очень сложно.

Осмыслим возможность вычисления подобных интегралов, кото- рые имеют такой общий вид:

где f(α) — функция, которая медленно изменяется на отрезке [α1,α2]; ϕ(α) — фазовая функция; q — большое число. Поскольку q есть боль- шое число, то, очевидно, что пока условие равенства нулю производ- ной от фазовой функции ϕ′(α) = 0, не выполняется, вклады в I от со- седних участков α будут практически компенсировать друг друга вследствие быстро осциллирующего характера exp(iqϕ(α)). Таким обра- зом, весь интеграл сводится к вкладам от окрестностей точек, в кото-

рых ϕ′(α) = 0. Эти точки называются точками стационарной фазы, а

метод, по которому вычисляют интеграл (9.150), называют методом стационарной фазы. Этот метод принадлежит к классу асимптотиче- ских методов вычисления интегралов [60].

Итак, согласно методу стационарной фазы [60, с. 55] приближен- ное значение интеграла (главный член асимптотики) (9.168) определя- ется выражением

где α0 — корень уравнения ϕ′(α) = 0. Вблизи стационарной точки α0 фаза ϕ(α) изменяется наиболее медленно. Знак показателя экспонен- ты совпадает со знаком второй производной ϕ″(α0).

Таким образом, если считать интеграл (9.168) суперпозицией коле- баний, то видим, что величина I пропорциональна амплитуде f(α0), которая вычислена в точке стационарной фазы, а фаза результи- рующего колебания определяется фазой также в стационарной точке. Кроме того, в выражение (9.169) входит величина ϕ″(α0), которая со- ответствует кривизне фазовой функции в стационарной точке. Итак, чем медленнее изменяется фаза ϕ(α) вблизи стационарной точки (т.е.

чем меньше величина ϕ′′(α0 ) ), тем больше участок интегрирования

αвокруг точки α0, для которой qϕ(α) ≈ const.

Вернемся к нашей задаче и вычислим интеграл (9.167). Как след-

ствие решения уравнения (cos(θ – α))′ = 0, на интервале α (–π/2, π/2) имеем одну стационарную точку α0 = θ. Вторая производная от фазо-

598

вой функции в стационарной точке равна –1. Таким образом, в соот- ветствии с методом стационарной фазы интеграл (9.167) определяет- ся формулой

Отсюда имеем выражение для характеристики направленности поло- сы шириной 2а с равномерным распределением скорости (υ0 = const) на ее поверхности:

Если ka << 1, т.е. характерный волновой размер полосы мал, то R(θ) ≈ ≈ 1, т.е. источник является ненаправленным. При этом полоса излуча-

ет цилиндрическую волну exp(ikr ) kr . С ростом величины ka появ-

ляются лепестки в диаграмме направленности. Предлагаем читателю с помощью ЭВМ построить ряд графиков функции R(θ) при разных величинах ka.

9.15. Возбуждение волновода точечным источником

При исследовании задачи о возбуждении волновода ис- точником звука важную роль играет математическая модель в виде точечного источника, который излучает гармонический с частотой ω сигнал в плоскопараллельном волноводе. Здесь, с одной стороны, имеем простую модель источника, а с другой — большинство других источников могут быть аппроксимированы совокупностью несколь- ких или множеством (вплоть до бесконечности) точечных источников.

Если поле создается гармоническим точечным источником, то за- дача сводится к определению функции Грина для уравнения Гельм- гольца в данной области.

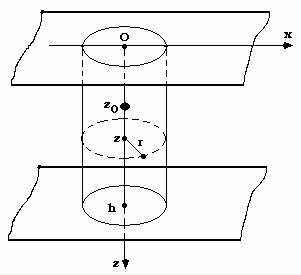
Пусть точечный источник размещен на расстоянии z0 от верхней границы волновода (рис. 9.24), т.е. его координаты (x0 = 0,y0 = 0,z0 ).

Будем считать, что границы волновода — локально-реагирующие (импедансные). Нам уже известно, что в таком волноводе могут суще- ствовать нормальные волны, конечное количество которых являются однородными, а остальные — неоднородными.

Поле давления p(r) в точке наблюдения r численно совпадает с функцией Грина

которая должна удовлетворять соответствующему уравнению Гельм- гольца, условиям на границах z = 0 и z = h , а также условию излуче- ния (т.е. волны распространяются от источника в направлении роста координаты r ).

Рис. 9.24. Точечный источник (точка z0 ) в плоскопараллельном волноводе

Поле точечного источника в волноводе имеет симметрию относи- тельно вертикальной оси, которая проходит сквозь источник. Поэтому удобно рассматривать это поле, используя цилиндрическую систему координат. Ее начало расположим на верхней поверхности волново- да, ось Oz направим вниз, рис. 9.24. Второй, после z , координатой точки в пространстве есть расстояние r в горизонтальной плоскости. От третьей координаты (угла в горизонтальной плоскости) акустиче- ское поле не зависит. Тогда функция

описывает поле давления в волноводе и удовлетворяет волновому уравнению

Существует несколько подходов к поиску поля точечного источни- ка в плоскопараллельном волноводе. Проведем наши исследования на основе представления поля в волноводе в виде совокупности нор- мальных волн. Фактически это означает, что мы используем решение однородного уравнения Гельмгольца, которое отвечает неоднородно- му уравнению (в данном случае — уравнению (9.174)) с соответст-

600