2.5 Поверхности второго порядка

В трехмерном пространстве с декартовой системой координат уравнение поверхности может быть задано в явной форме или в неявной форме

(42)

Если в уравнении (42) хоть одна из переменных x, y или z входит в квадрате (или две переменные перемножаются), то такая поверхность называется поверхностью второго порядка (точное определение см. [1]). Опишем несколько различных видов таких поверхностей.

Сферой радиуса R с центром в точке называется поверхность, образованная точками, удаленными на расстояние R от центра. Из формулы для расстояния между точками и получается уравнение сферы (рис. 25):

На рис. 26

Рис. 26	Рис. 27

Эллипсоид с полуосями и центром в начале координат (рис. 27) описывается уравнением

Если совпадают два параметра из трех, например, то уравнение

описывает эллипсоид вращения (в данном случае вокруг оси Z).

Если , то эллипсоид превращается в сферу радиуса R (рис. 26).

Эллиптический параболоид (рис. 28) описывается уравнением

Рис. 28	Рис. 29

Сечение горизонтальными плоскостями – эллипсы, сечения вертикальными плоскостями – параболы.

Если то параболоид называется параболоидом вращения (вокруг оси Z).

Уравнение

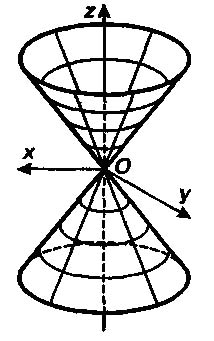
описывает конус (рис. 29).

Горизонтальные сечения – эллипсы, вертикальные сечения – гиперболы, а сечения плоскостями и – прямые и соответственно.

Уравнение

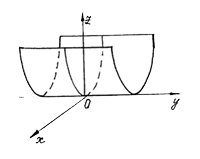
описывает гиперболический параболоид (рис. 30).⁴

Рис. 30

Горизонтальные сечения – гиперболы, вертикальные сечения – параболы, а сечения плоскостью – прямые

Уравнение

(43)

описывает однополостной гиперболоид (рис. 31).

Рис. 31	Рис. 32

Горизонтальные сечения – эллипсы, вертикальные сечения – гиперболы.

Уравнение

(44)

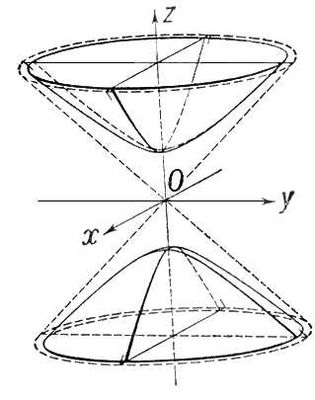
описывает двуполостной гиперболоид (рис. 32). Здесь тоже горизонтальные сечения – эллипсы, а вертикальные сечения – гиперболы.

Замечание. Другое распределение знаков в уравнениях (43), (44) меняет ориентацию поверхности относительно осей координат.

Если в уравнение поверхности не входит одна из трех переменных x, y или z, то поверхность называется цилиндрической, и соответствующая координатная ось параллельна этой поверхности.

Например, уравнение

описывает эллиптический цилиндр, в горизонтальных сечениях которого один и тот же эллипс (рис. 33), а уравнение описывает параболический цилиндр, в вертикальных (перпендикулярно оси y) сечениях которого парабола (рис. 34).

Рис. 33	Рис. 34

Уравнение касательной плоскости к поверхности, заданной уравнением (42) в точке , как известно (см. [1]), имеет вид

(45)

где

Нормалью (перпендикуляром) к поверхности в точке называется нормаль к касательной плоскости в этой точке. Следовательно,

Пример 39. Написать уравнение касательной плоскости к параболоиду вращения в точке с координатами

Решение.

Тогда

Следовательно, уравнение касательной плоскости:

◄

Пример 40. Найти линию пересечения параболоида и плоскости

Решение. Линию пересечения образуют точки, удовлетворяющие системе уравнений:

Исключая переменную z, получаем уравнение, описывающее проекцию этой линии на плоскость x0y.

А именно,

Это уравнение окружности с центром в точке радиуса (см. рис. 34).

Рис. 35

Кривую пересечения параметрически можно описать так: Или так:

◄

Пример 41. Касательная плоскость к параболоиду параллельна плоскости Найти точку касания.

Решение. Уравнение касательной плоскости к параболоиду в точке с координатами имеет вид (см. уравнение 45 и пример 39)

Так как эта плоскость параллельна плоскости , то

Тогда из уравнения параболоида получаем

◄