3 семестр_1 / Семестр_3_Лекция_14_15

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный технический университет им. H.Э.Баумана

Предмет:

Физика

Файл:

электромагнитной волны в вакууме равна c =

108 м/с и совпадает со значением ско-

.pdf

Скачиваний:

Добавлен:

10.02.2015

Размер:

193.92 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

Семестр 3. Лекции 14_15

Лекция 14-15. Электромагнитные волны.

Волновое уравнение для электромагнитного поля, его общее решение. Распространения элек-

тромагнитных волн. Энергия и импульс электромагнитного поля. Вектор Пойнтинга. Теорема Пойнтинга.

Рассмотрим уравнения Максвелла в вакууме, в условиях отсутствия зарядов и токов.

При ρ=0, j = 0 , ε=1, µ=1 уравнения в дифференциальной форме примут вид

∂B

divD = 0 ,

rotE = −

∂t

∂D

divB = 0 ,

rotH =

∂t

Учитываем материальные уравнения D = ε0 E ,

B = µ0 H и получаем систему уравнений

div (E ) = 0

(1)

∂H

(2)

rotE = −µ0

∂t

div (H ) = 0

(3)

∂E

(4)

rotH = ε0

∂t

∂

Начинаем преобразования уравнений (2) и (4):

(rotE ) = −µ

, откуда

∂t 2

∂t

∂E

∂2 H

rot

= −µ

(5)

0 ∂t 2

∂t

∂E

= −µ

∂

2 H

Т.к. из (4) следует, что

rotH , то равенство (5) примет вид rot

rotH

или

∂t

ε0

∂t 2

∂

rot (rotH )

= −ε

(6)

∂t 2

Но, как известно из лекции № 13 rot (rot (H )) = grad

(div (H ))

−

H , поэтому с учётом (3),

уравнение (6) равносильно уравнению

∂2 H

H =

(7)

∂t 2

∂H

= −

Аналогичные преобразования можно провести для вектора E : из (2) следует

rotE ,

∂t µ0

Семестр 3. Лекции 14_15

∂

∂H

(rot (H )) = rot

rot (rotE ),

из (4) следует ε

= rot

−

rotE

= −

0 ∂t 2

∂t

µ0

Учитывая (1), получаем rot (rot (E )) = grad (div

(E ))

− E = −

E , поэтому

∂2 E

E =

(8)

∂t 2

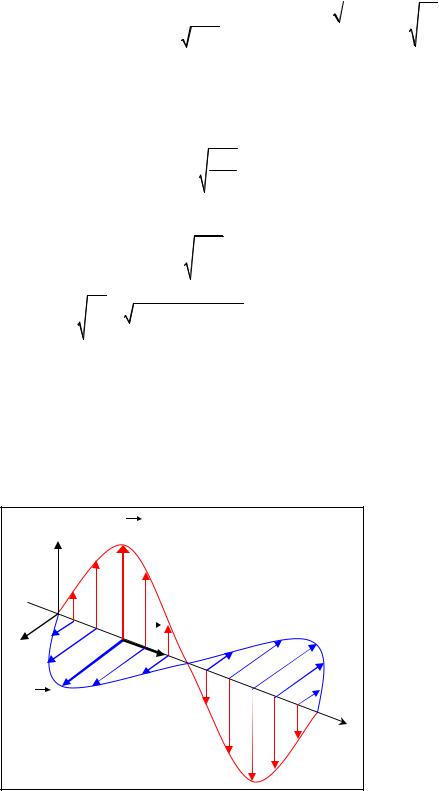
Полученные уравнения (7) и (8) имеют вид волнового уравнения – они описывают рас-

пространение плоских электромагнитных волн. Сразу можно сказать, что фазовая скорость

рости света в вакууме.

При распространении электромагнитных волн в среде с постоянными значениями ε и µ,

выражение для фазовой скорости примет вид v =

, где величина n = εµ на-

ε0 εµ0µ

εµ

зывается показателем преломления среды.

Замечание. Предположение о постоянстве значений ε и µ приводит к расхождению с опытными значениями показателя преломления. Например, для воды ε≈81 и µ≈1, что даёт значение рас-

чётное n≈9. Однако, экспериментально определено значение n≈1,5. Несовпадение объясняется возможной зависимостью ε и µ от частоты и других параметров волны.

Волновое уравнение является линейным, в том смысле, что любая линейная комбинация решений тоже является решением. Отсюда, как известно из предыдущего семестра, следует принцип суперпозиции для волновых полей – наложение волновых полей является волновым по-

лем. Поэтому выделяют «простейшие» волновые поля – поля (или волны), соответствующие определённым частотам. Такие «простейшие» волны, определенная частота которых постоян-

ная, называются монохроматическими.

Пример. Электромагнитная волна, частоты колебаний векторов в которой равны 1000 Гц и 2000

Гц является суперпозицией двух монохроматических волн с частотами 1000 Гц и 2000 Гц.♣

В декартовых координатах волновые уравнения (7) и (8) имеют вид

	2	∂2 H X
v
v		∂x2
		∂x2
		∂	2	HY
	2	∂		HY
v
v		∂x2
		∂x2
	2	∂2 H Z
v
v		∂x2
		∂x2

∂2 H

∂y

∂z

∂t

∂2 H

∂y

∂z

∂t

H Z

∂

∂y2

∂z 2

∂t 2

	2	∂2 EX
v
v		∂x2
		∂x2
	2	∂	2	E
	2	∂		E
, v				Y
, v		∂x2
		∂x2
	2	∂2 EZ
v
v		∂x2
		∂x2

∂2 EX

∂y

∂z

∂t

∂2 EY

∂y

∂z

∂t

∂

∂y2

∂z 2

∂t 2

Семестр 3. Лекции 14_15

Эти уравнения описывают распространение плоских волн. Пример записи решения для первых уравнений каждой из систем

H X = H 0 X sin (ωH t (kH ,r ) + αH ), EX = E0 X sin (ωE t (kE ,r ) + βH )

(индекс «Е» соответствует параметрам напряженности электрического поля, а «Н» - магнитно-

го) где в соответствующей волне (k ,r ) = kx x + k y y + kz z , r = ( x, y, z ) радиус-вектор точки, где

находится волна, а для координат волнового вектора k = (kx ,k y ,kz ) справедливо соотношение

							ω
k :=		= k 2		+ k 2	+ k 2	=		.
	k
	k
			x	y	z		v
							v

Знак «-» соответствует «убегающей» волне, а знак «+» - набегающей.

Обратим внимание на тот факт, что волновые уравнения для каждой из координат векто-

ров E и H независимы друг от друга, поэтому общее решение можно рассматривать как су-

перпозицию решений для координат векторов.

При этом решения волновых уравнений согласованы. Т.е. определённому решению од-

ного из волновых уравнений для какой-то координаты вектора напряжённости электрического поля соответствует определённое решение одного из волновых уравнений для координат векто-

ра напряжённости магнитного поля, и наоборот.

Поэтому можно искать решения, соответствующие, например, вектору E = (EX , EY , EZ ) .

Но согласно принципу суперпозиции волновых полей, решение, соответствующее вектору


E = (EX , EY , EZ ) можно найти как суперпозицию решений, соответствующих векторам

E1 = (EX ,0,0)	, E2 = (0, EY ,0) , E3 = (0,0, EZ ) .

Аналогично, можно искать решения по вектору напряжённости магнитного поля

H = (H X , HY , H Z ) .

Пример. Найдем решения для случая, когда волна движется вдоль оси z, а вектор напряжённо-

(ЕX ,0, ЕZ ) , зависящие только от z. Волна в

сти электрического поля имеет координаты E =

этом случае является суперпозицией волновых полей векторов E1 = (EX ,0,0)

и E3 = (0,0, EZ ) .

Система волновых уравнений в декартовых координатах примет вид

2 ∂2 EX

∂2 EX

∂z

∂t

2 ∂2 EZ

∂2 EZ

∂z

∂t

Так как ищем решения в виде волны, то будем предполагать, что в рассматриваемой об-

ласти нет постоянных во времени электрического и магнитного полей. Т.е. если при решении

Семестр 3. Лекции 14_15

получается постоянное значение какой-то координаты векторов E или H , то это значение можно считать равным нулю.

	∂EZ
Уравнение (1) div (E ) = 0 примет вид		= 0 , откуда E		не зависит от координат, но,
			Z
	∂z

возможно, зависит от времени. Но эта координата должна также удовлетворять волновому

∂2 E

уравнению v

. Поэтому E

= const - т.е. поле постоянное, откуда E

= 0 .

∂z 2

∂t 2

∂H

Из уравнения (2) rotE = −µ0

, с учётом EZ

= 0

∂t

∂H

∂

∂H

= −µ0

∂x

∂y

∂z

∂t

остаются равенства

∂H X

= 0,

∂EX

= −µ

∂HY

∂EX

= −µ

∂H Z

∂t

∂z

∂t

∂y

∂t

Координата H X не зависит от времени, но, так как она должна являться решением волнового уравнения

∂2 H

∂x

∂y

∂z

∂t

то H X = const , поэтому H X = 0 .

∂EX

∂y

Искомые координаты векторов E и H зависят только от z, следовательно, должно быть

= 0 , поэтому из третьего равенства следует		∂H Z		= 0 и, по аналогии, H		= 0
= 0 , поэтому из третьего равенства следует				= 0 и, по аналогии, H	Z	= 0
			∂t		Z
			∂t
	∂HY							∂E
Уравнение (3) div (H ) = 0 примет вид	∂HY		= 0 . Уравнение (4) rotH = ε					∂E
Уравнение (3) div (H ) = 0 примет вид	∂y		= 0 . Уравнение (4) rotH = ε				0	∂t
	∂y							∂t

∂

= ε

∂EX

∂x

∂y

∂z

∂t

даёт соотношение −

∂HY

= ε

∂EX

. Получаем систему

∂z

∂t

Семестр 3. Лекции 14_15

	∂EX		= −µ			∂HY
					0
∂z						∂t ,

−		∂HY		= ε0		∂EX
						∂t
		∂z

откуда можно опять получить волновые уравнения v2		∂2 HY	=	∂2 HY	и v2	∂2 EX	=	∂2 EX	.
откуда можно опять получить волновые уравнения v2		∂z 2	=	∂t 2	и v2	∂z 2	=		.
		∂z 2		∂t 2		∂z 2		∂t 2

Следовательно, вектору напряжённости электрического поля E1 = (EX ,0,0) соответству-

ет вектор напряженности магнитного поля H 2 = (0, HY ,0) .

Поэтому вектору E2	= (0, EY ,0) будет соответствовать вектор H1 = (H X ,0,0) .

Но векторам E3 = (0,0, EZ ) и H3 = (0,0, H Z ) не соответствует никакая плоская электро-
магнитная волна, распространяющая вдоль оси Z
	Заключение по результатам примера.
1) Плоская электромагнитная волна является поперечной.

Действительно, из примера следует, что продольные составляющие (вдоль направления движения волны - оси Z) векторов напряжённостей электрического и магнитного полей равны

нулю ЕZ = 0 и H Z	= 0 .

Векторы E = (ЕX ,0,0) и H = (0, HY ,0) направлены перпендикулярно друг другу и пер-

пендикулярно направлению движения волны. Если направление движения волны вдоль оси Z

задать волновым вектором k = (0,0,k ) , то можно сказать что тройка векторов (E , H ,k ) являет-

ся правой.

2) Колебания напряженностей электрического и магнитного полей в любой точке плоской вол-

ны происходят с одинаковой фазой.

Действительно, пусть решения волновых уравнений имеют вид

kE E0 cos (ωE t kE z + βE ) = −µ0ωH H 0 cos (ωH t kH z + αH )

Это равенство возможно, только если фазы волн равны с точностью до π.

Семестр 3. Лекции 14_15

Откуда ωE = ωH , т.е. колебания происходят с одинаковой частотой, и, так как фазовые

скорости одинаковые, то равны и волновые числа kE = kH .

Из равенства амплитуд k

E = µ

следует соотношение H

E =

ωE

E . Но

E 0 0

µ0

ωH µ0v

ε0µ0

фазовая скорость волны (в вакууме) v = c =

, поэтому H

E =

ε0

E .

ε0µ0

µ0

При распространении плоской электромагнитной волны в среде с постоянными значе-

ниями ε и µ, величины напряженностей магнитного и электрического полей связаны соотно-

шением

H = εε0 E . µµ0

Отношение амплитуд напряжённостей электрического и магнитного полей называется

волновым сопротивлением среды Z

µµ0

. Единица измерения Ом.

H 0

εε0

µ0

Для вакуума (ε=1, µ=1) Z

≈

4π 10-7

36π 109 = 120π ≈ 377 Ом.

ε0

Объёмная плотность энергии в плоской волне сумме объёмных плотностей энергии электриче-

ского и магнитного полей

w = wЭ + wМ .

Из соотношения амплитуд следует, что объёмные плотности энергии электрического и магнитного полей в плоской волне равны друг другу. Действительно,

	E
X
Y	k
Y
H	Z

		Семестр 3. Лекции 14_15
		H 2						2		E 2
	µµ	H 2		µµ	0	εε	0	2	εε	E 2
w =	0		=		0		0	E =	0		= w .
w =			=					E =			= w .
M	2			2		µµ0			2		Э
	2			2		µµ0			2

Таким образом, энергия плоской волны равномерно распределена на электрическую и

магнитную части. По аналогии с МКТ, иногда говорят, что плоская электромагнитная волна об-

ладает двумя степенями свободы.

Поэтому w = w + w		= µµ	H 2	= εε	E 2 . Или
Э	М	0		0
w = εε E 2		sin2 (ωt kz + α ) =				εε0 E02	(1 − cos (2 (ωt kz + α ))),
w = εε E 2		sin2 (ωt kz + α ) =					(1 − cos (2 (ωt kz + α ))),
0	0				2
					2

объёмная плотность энергии в плоской электромагнитной волне тоже является плоской волной,

но с удвоенной частотой. Фазовая скорость волны энергии равна v

ωЭ

2ω

= v фазовой ско-

kЭ

рости электромагнитной волны.

Средняя плотность энергии, переносимая плоской электромагнитной волной

< w >=

µµ

H 2

εε

E 2 .

Изменение объёмной плотности энергии электромагнитного поля в данной точке

∂w

∂E

∂H

= εε0

E ,

+ µµ0

H ,

∂t

Воспользуемся уравнениями Максвелла

∂B

∂H

∂D

∂E

rot (E ) = −

= −µµ

rot (H )

= j +

= j + εε

∂t

Откуда

∂H

∂E

µµ

= −rot (E ),

εε

= rot (H )− j .

∂t

Тогда

∂w

= E ,εε0

∂E

H ,µµ0

∂H

= (E ,(rot (H ) − j ))−

(H ,rot

(E ))

∂t

∂w

= (E ,rot

(H ))−

(H ,rot

(E ))− (E , j ) .

∂t

Используем оператор «набла»:

(E ,rot (H ))− (H ,rot (E )) = (E ,(

× H ))− (H ,( × E ))

Т.к. оператор «набла» - это оператор дифференцирования и для любого произведения

( f g )

= g ( f ) + f ( g ) ,

Семестр 3. Лекции 14_15

то ( ,(

E × H )) = − (E ,( × H )) + (

H ,( × E )) ,

т.е.

(E ,rot (

H )) − (H ,rot (E )) = −div (

E × H ) .

Поэтому

∂w

= −div (E × H )

− (E , j ).

∂t

Проинтегрируем это выражение по объёму некоторой области V, в которой есть электромаг-

нитное поле:

∂w

−∫∫∫

dV = ∫∫∫div (E × H )dV + ∫∫∫(E , j )dV

∂t

Если область не движется, то ∫∫∫

∂w

dV =

∫∫∫wdV =

, где W = ∫∫∫wdV энергия

∂t

электромагнитного поля в области V.

По закону Ома

j = γE или E = ρj , где ρ =

- удельное сопротивление среды. Поэтому

выражение (E , j ) = (ρj , j ) = ρj 2 - это дифференциальная форма закона Джоуля-Ленца. Тогда

∫∫∫(E , j )dV =

∫∫∫ρj 2 dV =

- мощность выделения теплоты (по закону Джоуля-Ленца) в области V.

По теореме Остроградского-Гаусса ∫∫∫div (E × H )dV = ∫∫

((E × H ),dS ),

где S – ориентированная наружу поверхность, являющаяся границей области V.

Вектор Π = (E × H ) (Π - буква «пи») называется вектором Пойнтинга (Джон Генри

Пойнтинг - британский физик (1852 - 1914)). Окончательно получим равенство, называемое

теоремой Пойнтинга

	dW
−		= ∫∫	(Π,dS )+	dQ	.
	dt
		S		dt

Скорость изменения энергии электромагнитного поля в некоторой области равна, с обратным знаком, сумме мощности выделения теплоты (по закону Джоуля-Ленца) и потока вектора Пойнтинга через границу области, ориентированную наружу.

		Семестр 3. Лекции 14_15
Если в области нет тепловыделения dQ = 0 , то в случае, когда векторное поле Π на гра-
		dt
			dW > 0 - энергия облас-
нице S направлено внутрь области поток отрицателен ∫∫ (Π ,dS ) < 0 , а			dW > 0 - энергия облас-
		S	dt
		S
ти увеличивается. И наоборот, если поток вектора Пойнтинга направлен наружу из области V,
		dW < 0 - энергия в области убывает.
т.е. ∫∫ (Π ,dS ) > 0 , то		dW < 0 - энергия в области убывает.
S		dt
S
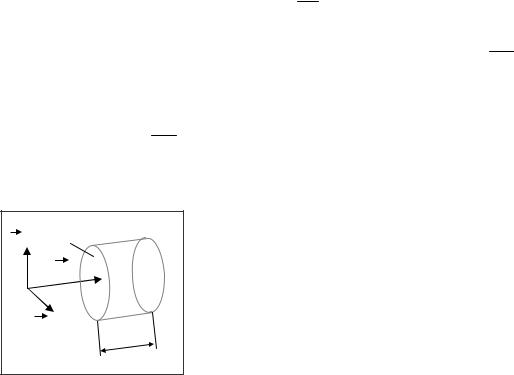
Рассмотрим область, в которой распространяется плоская электромагнитная волна.
		Предположим, что в области нет выделения теплоты по закону
S		Джоуля-Ленца. Выделим в области малую площадку S , перпенди-
E
П		кулярную вектору Пойнтинга и найдём поток вектор Пойнтинга
П
		через эту площадку за малое время dt. Так как скорость волны объ-
H		ёмной плотности энергии равна фазовой скорости электромагнит-
H	v dt
	v dt	ной волны v, то количество энергии, прошедшей через площадку

		равно энергии в объёме прямого цилиндра с площадью основания
S и высотой vdt:

				wdV		wS vdt
∫∫	(Π ,dS ) = −	dW	= −		= −		= −wvS
		dt		dt
SЦИЛ						dt

Поверхность цилиндра ориентирована наружу, а вектор Пойнтинга направлен внутрь цилиндра,

поэтому ∫∫ (Π,dS ) = −ΠS . Тогда из равенства −ΠS = −wvS следует Π = wv . В векторном

SЦИЛ

виде можно записать равенство

Π = wv .

(Из этой формулы следует, что вектор Пойнтинга направлен по движению волны.)

Следовательно, вектор Пойнтинга – это вектор Умова-Пойнтинга, соответствующий электромагнитной волне. Поэтому физический смысл вектора Пойнтинга состоит в том, что он указывает направление потока энергии, а его величина равна плотности мощности потока энер-

гии.

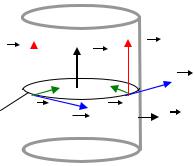
Пример. Рассмотрим часть цилиндрического проводника длиной l и площадью попереч-

ного сечения S , по которой протекает постоянный электрический ток. Предположим, что вели-

чина плотности тока j постоянна в сечении проводника, поэтому сила тока равна

I = jS .

Семестр 3. Лекции 14_15

По закону Ома j = γE =

E , где ρ - удельное сопротивление

проводника. На поверхности проводника вектор H направ-

лен по касательной к силовой линии Г, а его величина

H =

2πr

где r – радиус проводника. Направления H и

j согласованы

правилом буравчика, и направлены перпендикулярно друг другу, но

j E , поэтому H E . То-

гда на поверхности проводника вектор Пойнтинга Π = E × H направлен вглубь проводника, т.е.

против вектора dS . Найдём поток вектора Пойнтинга через (боковую) поверхность проводни-

ка.

dS = − ∫∫ EHdS .

∫∫ (Π ,dS ) = − ∫∫

SБОКОВ

Здесь учтено, что

= EH sin 900 = EH и что векторы dS и Π направлены противоположно.

Т.к. E = jρ =

ρ , SБОКОВ = 2πrl , то

∫∫ (Π,dS ) = −EH

∫∫ dS = −

2πrl = −I 2ρ

= −I 2 R ,

2πr

SБОКОВ

где R = ρ

электрическое сопротивление проводника. Итак, поток вектора Пойнтинга через

боковую поверхность проводника равен по величине мощности тепловыделения в проводнике

(по закону Джоуля-Ленца):


					∫∫	(Π,dS ) = −	dQ	.
					∫∫	(Π,dS ) = −		.
				SБОКОВ			dt
				SБОКОВ
	dW
Следовательно, −	dW	= ∫∫	(Π,dS )+	dQ	= 0 - энергия электромагнитного поля в проводнике не
Следовательно, −	dt	= ∫∫	(Π,dS )+		= 0 - энергия электромагнитного поля в проводнике не
	dt	S		dt
		S

меняется.♣

Рассмотрим в некоторой инерциальной системе отсчёта плоскую электромагнитную вол-

ну, движущуюся вдоль оси Z. Следовательно, вектор Пойнтинга Π тоже направлен вдоль оси

Z. Пусть SZ - малая площадку, перпендикулярная оси Z (и вектору Пойнтинга). Предположим,

что волна полностью поглощается веществом этой площадки. Как известно, в электромагнит-

ном поле на тела действуют силы, создающие давление, равное по величине объёмной плотно-

сти энергии p=w. Поэтому величина силы, действующей на площадку равна F=pSZ. Вектор этой силы направлен перпендикулярно площадке в направлении движения волны, т.е. вдоль оси Z,

1 / 21 2 > Следующая >>>

Соседние файлы в папке 3 семестр_1

#
10.02.2015163.69 Кб17Семестр_3_Лекция_08.pdf
#
10.02.2015172.87 Кб17Семестр_3_Лекция_09_10.pdf
#
10.02.2015162.65 Кб18Семестр_3_Лекция_11.pdf
#
10.02.2015164.56 Кб17Семестр_3_Лекция_12.pdf
#
10.02.2015157.69 Кб18Семестр_3_Лекция_13.pdf
#
10.02.2015193.92 Кб17Семестр_3_Лекция_14_15.pdf
#
10.02.2015131.55 Кб16Семестр_3_Лекция_16.pdf
#
10.02.2015134.8 Кб16Семестр_3_Лекция_17.pdf
#
10.02.2015284.87 Кб15Семестр_3_Лекция_18_19.pdf
#
10.02.2015107.83 Кб16Семестр_3_Лекция_20.pdf
#
10.02.2015190.91 Кб17Семестр_3_Лекция_21.pdf