Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный технический университет им. H.Э.Баумана

Предмет:

Физика

Файл:

3 семестр_1 / Семестр_3_Лекция_21

.pdf

Скачиваний:

Добавлен:

10.02.2015

Размер:

190.91 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

Семестр 3. Лекция 21

Лекция 21. Дифракция света.

Принцип Гюйгенса-Френеля. Метод зон Френеля. Векторная диаграмма.

Дифракция от круглого отверстия и круглого диска. Дифракция Фраунгофера от щели. Предельный переход от волновой оптики к геометрической.

Дифракция – это явление отклонения от прямолинейного распространения света, если оно не может быть следствием отражения, преломления или изгибания световых лучей, вызванным пространственным изменением показателя прелом-

ления. При этом отклонение от законов геометрической оптики тем меньше, чем меньше длина волны света.

Замечание. Между дифракцией и интерференцией нет принципиального различия.

Оба явления сопровождаются перераспределением светового потока в результате суперпозиции волн.

Примером дифракции может служить явление при падении света на непро-

зрачную перегородку с отверстием. В этом случае на экране за перегородкой в области границы геометрической тени наблюдается дифракционная картина.

Принято различать два вида дифракции. В случае, когда падающую на пере-

городку волну можно описать системой параллельных друг другу лучей (напри-

мер, когда источник света находится достаточно далеко), то говорят о дифракции Фраунгофера или дифракции в параллельных лучах. В остальных случаях говорят о дифракции Френеля или дифракции в расходящихся лучах.

При описании явлений дифракции необходимо решить систему уравнений Максвелла с соответствующими граничными и начальными условиями. Однако,

нахождения такого решения в большинстве случаев является весьма затрудни-

тельным. Поэтому, в оптике, часто применяют приближённые методы, основан-

ные на принципе Гюйгенса в обобщенной формулировке Френеля или Кирхгофа.

Принцип Гюйгенса.

Формулировка принципа Гюйгенса. Каждая точка среды, до которой в неко-

торый момент времени t дошло волновое движение, служит источником вторич-

ных волн. Огибающая этих волн даёт положение фронта волны в следующий

2		Семестр 3. Лекция 21
близкий момент времени t+dt. Радиусы вторичных волны равны произведению
фазовой скорости света на интервал времени r = v dt .
			Иллюстрация этого принци-
		Вторичные	па на примере волны падающей
		Вторичные
		волны	на непрозрачную перегородку с
		волны
			отверстием показывает, что волна
			проникает в область геометриче-
		Границы	ской тени. Это является проявле-
		геометрической	нием дифракции.
	Фронт волны	тени	Однако, принцип Гюйгенса не да-
		тени	Однако, принцип Гюйгенса не да-
			ёт оценок интенсивности волн,
распространяющихся в различных направлениях.
Принцип Гюйгенса-Френеля.
Френель дополнил принцип Гюйгенса представлением об интерференции вторич-
ных волн. По амплитудам вторичных волн с учётом их фаз можно найти ампли-
туду результирующей волны в любой точке пространства.
	Каждый малый элемент волновой поверхности является источником вто-
ричной сферической волны, амплитуда которой пропорциональна величине эле-
мента dS, и уравнение которой вдоль луча имеет вид

dA = K (θ) a0 dS cos (ωt − kr + α ) r

здесь a0 - коэффициент, пропорциональный амплитуде колебаний точек на волно-

вой поверхности dS, K (θ) - коэффициент, зависящий от угла θ лучом и вектором

	π
dS , такой, что при θ = 0 он принимает максимальное значение, а при θ →		- ми-
	2

нимальное (близкое к нулю).

Результирующее колебание в некоторой точке наблюдения Р тогда опреде-

ляется аналитическим выражением принципа Гюйгенса-Френеля, которое вывел Кирхгоф:

AP = ∫∫K (θ) r0 cos (ωt − kr + α) dS

	Семестр 3. Лекция 21		3
		Интеграл берётся по волновой поверхно-
		Интеграл берётся по волновой поверхно-
dS		сти, зафиксированной в некоторый мо-
		сти, зафиксированной в некоторый мо-
θ		мент времени. Для свободно распростра-
	луч	мент времени. Для свободно распростра-
	луч	няющейся волны значение интеграла не
		няющейся волны значение интеграла не
		зависит от выбора поверхности интегри-
		рования S.
		Явное вычисление по этой формуле
		Явное вычисление по этой формуле
довольно трудоёмкая процедура, поэтому на практике можно применять прибли-
жённые методы нахождения этого интеграла.

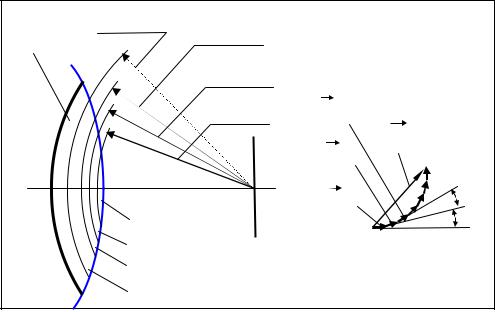
				Для нахождения амплитуды
		b+4 (λ/2)		колебаний в точке наблюдения P
зона № 4				колебаний в точке наблюдения P
зона № 4
зона № 3			b+3(λ/2)	всю волновую поверхность S можно
зона № 3
зона № 2			b+2(λ/2)	разбить на участки или зоны Френе-
зона № 1			b+λ/2	ля. Предположим, что мы наблюда-
зона № 1			b+λ/2
и т.д.				ем дифракцию в расходящихся лу-
и т.д.
				чах (дифракцию Френеля), т.е. рас-
L		O	P	сматриваем сферическую, распро-
L	a	O	P
	a	rm		страняющуюся от некоторого ис-
		rm		страняющуюся от некоторого ис-
				точника L. Пусть волна распростра-
		hm		няется в вакууме.
	a		b	Зафиксируем волновую по-
				Зафиксируем волновую по-
				верхность в некоторый момент вре-
мени t. Пусть радиус этой поверхности равен a. Линия LP пересекает эту поверх-
ность в точке О. Предположим, что расстояние между точками О и Р равно b. От

точки Р последовательно откладываем сферы, радиусы которых Rm = b + m λ . Две

соседние сферы «отсекают» на волновой поверхности кольцевые участки, назы-

ваемые зонами Френеля. (Как известно, две сферы пересекаются по окружности,

лежащей в плоскости, перпендикулярной прямой, на которой лежат центры этих

Семестр 3. Лекция 21

сфер). Найдём расстояние от точки О до границы зоны с номером m. Пусть радиус внешней границы зоны Френеля равен rm. Т.к. радиус поверхности равен a , то

	r 2	= a2	− (a − h		)2 = 2ah − h2 .
	m			m			m m
2			λ 2			2			λ 2	2
При этом одновременно, rm	= b + m			− (b + hm )			= mbλ +	m		− 2bhm − hm .
При этом одновременно, rm	= b + m			− (b + hm )			= mbλ +	m		− 2bhm − hm .
			2						2

λ 2

mbλ + m

Поэтому

2ahm − hm

= mbλ + m

− 2bhm

− hm , откуда hm

(a + b )

Для длин волн видимого диапазона и не очень больших значений номеров m

можно пренебречь слагаемым m

по сравнению с mλ. Следовательно, в этом

случае h

mbλ

и для квадрата радиуса получаем выражение

2 (a + b )

mbλ

= 2ah − h

= 2a

−

, в котором опять можно пренебречь последним

(a + b )

(a + b)

слагаемым. Тогда радиус m-й зоны Френеля (для дифракции в расходящихся лу-

чах)

abλ

rm = m (a + b) .

Следствие. Для дифракции в параллельных лучах (дифракции Фраунгофера) ра-

диус зон Френеля получается предельных переходом a→∞.

rm = mbλ .

Теперь сравним площади зон Френеля. Площадь сегмента сферической по-

верхности, лежащей внутри m-й зоны, как известно, равна S (m ) = 2πahm . Зона с но-

мером m заключена между границами зон с номерами m и m-1. Поэтому её пло-

щадь равна

				λ	2
				λ
		mbλ + m
		mbλ + m
S = S (m ) − S (m −1) = 2πa (h − h ) = 2πa				2
S = S (m ) − S (m −1) = 2πa (h − h ) = 2πa			2 (a + b )
m	m m−1		2 (a + b )
m	m m−1

					λ 2
	(m −1)bλ +		(m	−1)
	(m −1)bλ +		(m	−1)
−					2	.
−		(a + b )				.
2		(a + b )

Семестр 3. Лекция 21

			λ	2
				2

	bλ + (2m −1)
	bλ + (2m −1)		2
После преобразований выражение примет вид Sm	= 2πa		2
После преобразований выражение примет вид Sm	= 2πa	2 (a + b )
		2 (a + b )

	(2m −1)		λ 2		πabλ
Если пренебречь величиной				, то из выражения Sm =		следу-
					(a + b)
	2	(a + b )	2

ет, что при небольших номерах площадь зон не зависит от номера m.

Нахождение результирующей амплитуды в точке производится следующим образом. Т.к. излучаемые вторичные волны являются когерентными и расстояния

от соседних границ до точки Р отличаются на половину длины волны, то разность фаз колебаний от вторичных источников на этих границах, приходящих в точку Р равна π (как говорят, колебания приходят в противофазе). Аналогично, для любой точки какой-нибудь зоны обязательно найдётся точка в соседней зоне, колебания от которой приходят в Р в противофазе. Величина амплитуды волнового вектора пропорциональна величине площади зоны AP K (θ) Sm . Но площади зон одинако-

вые, а с ростом номера m возрастает угол θ, поэтому величина K (θ) убывает. По-

этому можно записать упорядоченную последовательность амплитуд

A1 > A2 > A3 > ... > Am−1 > Am > Am+1 > ... . На амплитудно -векторной диаграмме с учётом

разности фаз эта последовательность изображается противоположно направлен-

ными векторами, поэтому

b + n	b+3
зона № 1	b+3
зона № 1
	b+2
	b+	A1.3
		A1.3
		A1.2	A1.Σ
O		A1.2
O
	P	A1.1	δ
	P	A1.1	δ
зона № 1.1			δ
зона № 1.2
зона № 1.3
зона № 1.n и т.д.

6 Семестр 3. Лекция 21

AP = A1 − A2 + A3 − ... ± Am −1 Am ± Am+1 ...

Разобьем первую зону на большое количество N внутренних зон таким же,

как и выше, образом, но теперь расстояния от границ двух соседних внутренних

зон до точки Р будут отличаться на малую величину = λ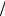 2 . Поэтому разность

фаз волн, приходящих волн в точку Р будет равна малой величине δ = k L = 2π .

На амплитудно-векторной диаграмме вектор амплитуды от каждой из внутренних зон будут повернут на малый угол δ относительно предыдущего, Поэтому ампли-

туде суммарного колебания от нескольких первых внутренних зон будет соответ-

ствовать вектор A1.Σ соединяющий начало и конец ломаной линии. При увеличе-

нии номера внутренней зоны суммарная разность фаз будет нарастать, и на гра-

нице первой зоны станет равной π. Это означает, вектор амплитуды от последней

внутренней зоны A1.N направлен противоположно вектору амплитуды от первой

внутренней зоны A1.N . В пределе бесконечно большого числа внутренних зон эта ломаная линия перейдет в часть спирали.

		Амплитуде колебаний от пер-
	F	вой зоны Френеля тогда будет
A1	F
A1	A3
	A∞	соответствовать вектор A1 , от
	A2
	A2	двух зон - A и т.д. В случае,
		2

если между точкой Р и источником света нет никаких преград, из точки наблюде-

ния будет видно бесконечное число зон, поэтому спираль будет навиваться на точку фокуса F. Поэтому свободной волне с интенсивностью I0 соответствует

вектор амплитуды A∞ , направленный в точку F.

Из рисунка видно, что для амплитуды от первой зоны можно получить оцен-

ку A1 = 2 A∞ , поэтому интенсивность от первой зоны I1 = 4I0 - в 4 раза больше ин-

тенсивности падающей волны. Равенство A1 = 2 A∞ можно трактовать и по-другому.

Если для бесконечного числа открытых зон суммарную амплитуду записать в ви-

де

Семестр 3. Лекция 21

A∞

− A2

− A4

+ ... +

m−1

− Am

m+1

+ ...

(m – четное число), то из A = 2 A		следует оценка A ≈	Am−1 + Am+1	.
(m – четное число), то из A = 2 A		следует оценка A ≈		.
1	∞	m	2
			2

Замечание. Если каким-то образом изменить фазы колебаний в точке Р от чётных зон или нечётных на π, или закрыть чётные или нечётные зоны, то суммарная ам-

плитуда увеличится по сравнению с амплитудой открытой волны. Таким свойст-

вом обладает зонная пластинка - плоскопараллельная стеклянная пластинка с выгравированными концентрическими окружностями,

радиус которых совпадает с радиусами зон Френеля. Зонная пла-

стинка «выключает» чётные либо нечётные зоны Френеля, что при-

водит к увеличению интенсивности света в точке наблюдения.

Дифракция на круглом отверстии.

Рассуждения, приведённые выше, позволяют сделать вывод, что амплитуда колебания в точке Р зависит от числа зон Френеля. Если для точки наблюдения открыто нечётное число зон Френеля, то в этой точке будет максимум интен-

сивности. Если открыто чётное число зон – то минимум.

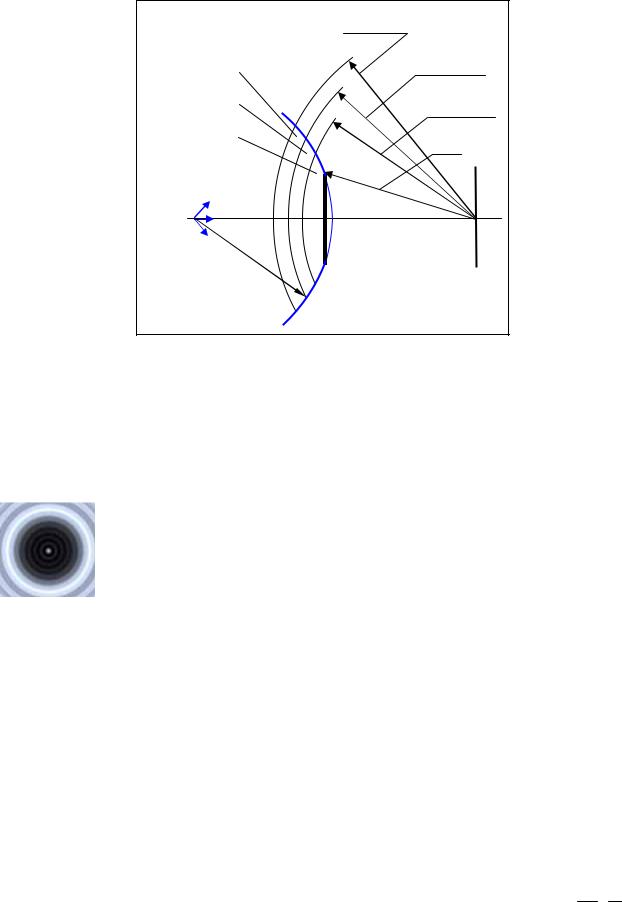
Дифракционная картина от кругло-

го отверстия имеет вид чередующихся светлых и тёмных колец.

При увеличении радиуса отверстия (и

увеличения числа зон Френеля) чередование тёмных и светлых колец будет на-

блюдаться только вблизи границы геометрической тени, а внутри освещённость практически не будет меняться.

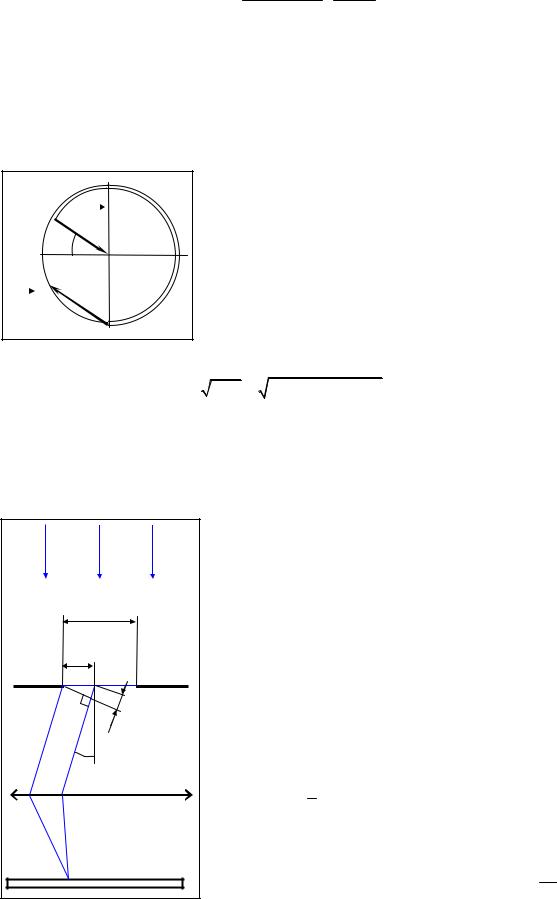
Дифракция на малом диске.

Рассмотрим схему опыта, в котором на пути световой волны расположен непрозрачный круглый диск, радиус которого соизмерим с радиусами первых зон Френеля.

Для рассмотрения дифракционной картины помимо обычных зон построим дополнительные зоны от края диска.

8	Семестр 3. Лекция 21
	b+3 (λ/2)
зона № 3		b+2(λ/2)
зона № 3
зона № 2		b+(λ/2)
зона № 1		b
и т.д.
L	O	P
	a

Зоны Френеля от края диска будем строить по прежнему принципу - рас-

стояния от границ двух соседних зон до точки наблюдения отличаются на поло-

вины длины волны. Амплитуда в точке наблюдения

− A2

− A4

+ ... +

m−1

− Am

m+1

+ ... .

с учётом оценки A ≈	Am−1 + Am+1	будет равна A =	A1	. Следовательно, в

m	2	P	2

точке наблюдения, в центре геометрической тени всегда будет свет-

лое пятно – максимум интенсивности. Это пятно называется пятном

Пуассона.

Замечание. Если диск закрывает только часть обычной первой зоны Френеля, то на экране не будет тени.

Пример. На непрозрачный диск диаметром D=0,5 см нормально падает плоская монохроматическая волна, длина которой λ=700 нм. Найти диаметр отверстия в центре диска, при котором интенсивность света в точке Р экрана (на оси системы)

будет равна нулю. Расстояние между диском и экраном равно L=2,68 м.

Решение. Найдём число обычных зон Френеля, которые закрыты диском. Номер

1 D 2

зоны найдём из формулы для радиуса при дифракции Фраунгофера m =

Lλ 2

Семестр 3. Лекция 21

−3

m =

−7

≈ 3,33 .

2,68 7 10

Т.е. диск закрывает 3 целых зоны и еще одну треть. Построим спираль Френеля.

Граничной точке этой части в 3,33 зоны соответствует угол наклона к горизонта-

ли, равный 300. Все остальные зоны открыты, поэтому вектор амплитуды A

,33

на-

правлен от граничной точки зоны Френеля в точку F. Чтобы в точке наблюдения

Р интенсивность была равной нулю, надо, чтобы вектор

A3,33

амплитуды света из отверстия AОТВ был равным по дли-

300

не, но противоположным по направлению вектору A3,33 .

Следовательно, он также должен быть наклонен к гори-

AОТВ

зонтали под углом в 30 . В этом случае отверстие долж-

но открывать 1,67 части зоны Френеля. Для m=1,67 получаем радиус отверстия

= mλL = 1,67 7 10−7

2,68 ≈ 1,77 10−3 м.♣

ОТВ

	Дифракция Фраунгофера от щели.
Рассмотрим дифракционную картину от узкой длинной щели шириной b, на
которую нормально падает плоская волна. Элементарные участки волнового
	фронта в форме узких длинных полосок, параллельных
	краям щели, становятся источниками вторичных ци-
	линдрических волн. Разобьем волновую поверхность в
b	щели на маленькие участки dx, каждый из них в точке
	щели на маленькие участки dx, каждый из них в точке
x	P создает колебание
	dA = Ka0 cos (ωt − k )
	Где = x sin ϕ - геометрическая разность хода лучей от
	края щели и от луча на расстоянии x от края. Здесь
ϕ	множителя 1 в амплитуде нет, поскольку рассматри-
	множителя 1 в амплитуде нет, поскольку рассматри-
	r
	ваются плоские волны. Каждая полоска шириной dx
P		= A0 dx , где А
	даёт одинаковый вклад амплитуды Ka	= A0 dx , где А	0	–
	0	b	0
		b
амплитуда волны.

Семестр 3. Лекция 21

Тогда для всей щели A

= b

A0 cos

(ωt − k ( x sin ϕ))dx = −

sin (ωt − k ( x sin ϕ)) b

∫

bk sin ϕ

= −

(sin (ωt − k

(b sin ϕ)) − sin (ωt )) =

bk sin ϕ

= −

−

cos

ωt − k (b sin ϕ)

+ cos

ωt

bk sin ϕ

= −

2 A0

kb sin ϕ

ωt −

k (b sin ϕ)

cos

bk sin ϕ

2 A0

sin

kb sin ϕ

(b sin ϕ)

cos

ωt −

bk sin ϕ

С учетом k = 2π получаем амплитуду колебания в точке Р

sin

b sin ϕ

= A

P 0

b sin

При ϕ<<1 амплитуда в точке Р равна амплитуде падающей волны AP 0 = A0 , а при

выполнении условия b sin ϕ = mλ , где m – целое число, амплитуда равна нулю

AP 0

= 0 . Поэтому для интенсивности волны в направлении задаваемом углом ϕ

sin

b sin ϕ

= I

. При этом

b sin ϕ

I/I0

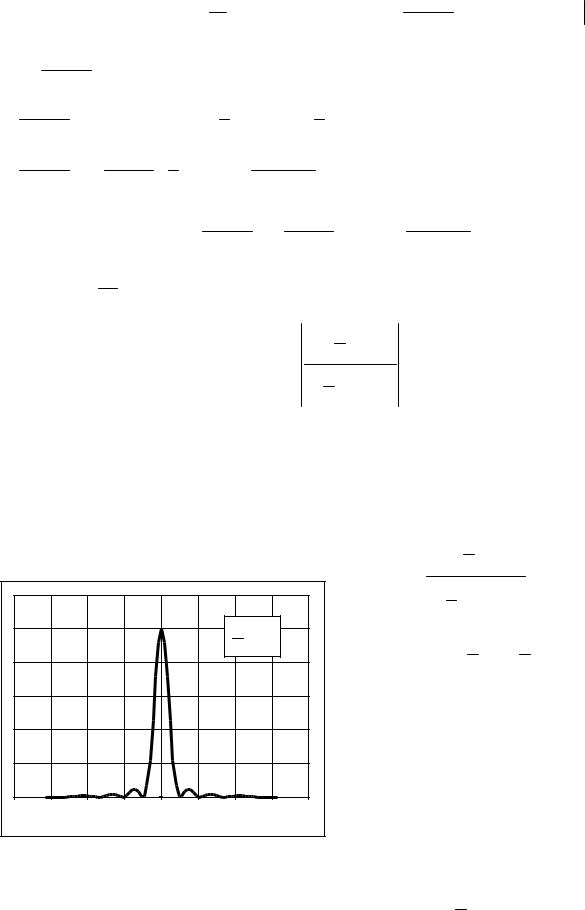
b = 4 .

− π < ϕ < π .

0,8

0,6

При ϕ=0 находится центральный

0,4

максимум Iϕ = I0 , значительно превос-

0,2

ходящий по величине остальные мак-

-2

-1,5

-1

-0,5

0,5

1,5

симумы.

Условие минимумов b sin ϕ = mλ ,

где m – целое число. Центральный максимум ограничен с двух сторон первыми

минимумами, положение которых задаётся углом sin ϕ = ± λ .

1 / 21 2 > Следующая >>>

Соседние файлы в папке 3 семестр_1

#
10.02.2015193.92 Кб17Семестр_3_Лекция_14_15.pdf
#
10.02.2015131.55 Кб16Семестр_3_Лекция_16.pdf
#
10.02.2015134.8 Кб16Семестр_3_Лекция_17.pdf
#
10.02.2015284.87 Кб15Семестр_3_Лекция_18_19.pdf
#
10.02.2015107.83 Кб16Семестр_3_Лекция_20.pdf
#
10.02.2015190.91 Кб17Семестр_3_Лекция_21.pdf
#
10.02.2015144.99 Кб16Семестр_3_Лекция_22_23.pdf
#
10.02.2015116.65 Кб27Семестр_3_Лекция_24.pdf
#
10.02.2015181.8 Кб22Семестр_3_Лекция_25.pdf