
3 семестр_1 / Семестр_3_Лекция_04
.pdf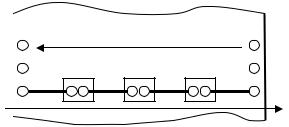
Семестр 3. Лекция 4.
Лекция 4. Электростатическое поле в диэлектрике.
Электрический диполь в электростатическом поле. Поляризация диэлектриков. Электроста-
тическое поле в диэлектрике. Поляризованность. Свободные и связанные заряды. Связь поля-
ризованности с плотностью связанных зарядов. Вектор электрического смещения. Обобщение теоремы Гаусса. Поле на границе раздела диэлектриков.
Все вещества состоят из атомов и молекул, которые, в свою очередь, состоят из заря-
женных частиц. Эти заряженные частицы находятся в постоянном движении, поэтому при классическом описании их движения будут рассматриваться усреднённые по времени величины.
Если в веществе есть электрические заряды, способные относительно свободно перемещаться в пределах тела даже под действием слабого электрического поля, то такие вещества относятся к так называемому классу проводников. Соответственно, вещества, в которых нет «свободно» движущихся зарядов (при обычных условиях) относятся к диэлектрикам.
Замечание. Это деление на классы проводников и диэлектриков весьма условно. Некото-
рые вещества, являющиеся проводниками в определённых условиях, становятся диэлектриками
в других, и наоборот.
Замечание. В проводниках, находящихся в электрическом поле, суммарное внутреннее
электрическое поле характеризуются нулевой напряженностью. В диэлектриках напряженность суммарного поля отлична от нуля.
Рассмотрим поведение диэлектриков в электрическом поле.
Заряды, не входящие в состав вещества, будем называть сторонними (но они могут на-
ходиться внутри вещества). Эти заряды создают электрическое поле, которое будем называть
внешним.
В диэлектрике при нормальных условиях нет свободно движущихся носителей зарядов.
Все заряды, из которых состоит диэлектрик, связаны друг с другом. Их называют связанными.
Электрические заряды образуют молекулы. Если в отсутствии внешнего электрического поля электрические заряды в молекуле пространственно разделены, то молекула называется поляр-
ной, в противном случае – неполярной. |
|
||||||||||||||||||||||||||
|
|
|
|
Во внешнем поле полярная молекула вытягивается вдоль поля, а полярная разворачива- |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ется. Можно приближенно считать, что крайние |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
связанные заряды двух соседних диполей в глубине |
|
|
-q′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+q′ |
диэлектрика взаимно компенсируются, но заряды, |
|||||||||
|
|
|
|
|
|
|
|
|
|
E′ |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
расположенные вблизи поверхности диэлектрика |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ничем не скомпенсированы. Эти некомпенсирован- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ные заряды создают дополнительное электрическое |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
||||
1

Семестр 3. Лекция 4.
поле внутри диэлектрика, которое изменяет внешнее. Это явление разделения связанных заря-
дов и появления дополнительного поля называется поляризацией диэлектрика.
Теперь опишем поляризацию количественно.
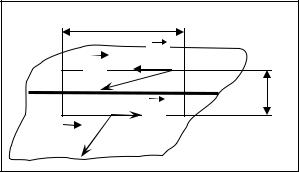
В простейшем случае молекулу можно представить как два одинаковых по величине, но
|
|
|
противоположных по знаку заряда. Такая систе- |
|
|
|
q |
||
|
p |
ма зарядов называется диполь. Электрическим |
||
|
F+ |
|||
|
|
|
|
|
|
|
α |
дипольным моментом называется векторная ве- |
|
|
|
|
|
|
|
|
E |
|
|
|
|
личина p = qL , где q – величина заряда, L – рас- |
||
F− |
-q |
|
|
|
|
|
стояние между зарядами. (Единица измерения |
||
|
|
|
||
|
|
|
Кл м). |
|
|
|
|
|
|
Вектор момента p направлен от отрицательного заряда к положительному.
На диполь, помещенный в электрическое поле, действует момент пары сил, величина которого
M = F+ L sin α = qEL sin α = pE sin α
В векторном виде
M = p × E
В состоянии равновесия диполя вектор дипольного момента p параллелен вектору напряжен-
ности E .
В отсутствии внешнего поля в диэлектрике с полярными молекулами, диполи ориенти-
рованы хаотически. В диэлектрике, находящемся в электростатическом поле, в состоянии рав-
новесии диполи преимущественно расположены вдоль поля.
Рассмотрим в диэлектрике некоторый физически малый объем величиной V. Введем век-
тор поляризованности вещества
∑N pi
P = i =1 . V
Единица измерения Кл/м2. В однородном изотропном диэлектрике этот вектор направлен па-
раллельно вектору напряженности, поэтому можно записать
P = æε0 E .
Безразмерный параметр æ называется коэффициентом поляризуемости или диэлектрической восприимчивости вещества.
Рассмотрим тонкий косой цилиндр, ось которого параллельна вектору напряженности внешне-
го поля.
2

|
|
Семестр 3. Лекция 4. |
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
∑ pi |
|
Nq′L |
|
q′ |
|
σ′ |
|
pN |
P = |
i =1 |
= |
= |
= |
|||
|
|
|
|
||||||
|
|
|
|
|
|||||
|
|
|
V |
|
SNL cos α |
|
S cos α |
|
cos α |
|
p2 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
||
p1 |
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
|
α |
где q′ - величина связанного заряда. Обратите вни- |
|||||||
|
|
мание: величина вектора не зависит от количества |
|||||||
суммируемых диполей – она определяется только поверхностной плотностью связанного заря- |
|||||||||
да. |
|
|
|
|
|
|
|
|
|
Отсюда получаем для нормальной составляющей вектора |
|
|
|
|
|
||||
P = P cos α = σ′ .
n
Нормальная составляющая вектора поляризованности равна поверхностной плотности связан-
ного заряда.
Теперь найдём поток вектора поляризованности через некоторую малую поверхность S.
|
|
||||||||
Φ P = ∫∫(P,dS ) = ∫∫ |
|
P |
|
cos αdS ≈ |
|
P |
|
cos αS = σ′S = q′ . |
|
|
|
|
|
||||||
S |
S |
||||||||
Таким образом, поток вектора поляризованности через некоторую малую площадку равен ве-
личине связанного заряда, создающего этот вектор.
Рассмотрим поток этого вектора через некоторую замкнутую ориентированную поверх-
ность внутри диэлектрика
|
|
|
|
|
cos αdS = ∫∫ σ′dS . |
∫∫ (P,dS ) = ∫∫ |
|
P |
|
||
|
|
||||
S |
S |
|
|
|
S |
Предположим, что вектор поляризованности направлен наружу, т.е. внутри поверхности сум-
марный связанный заряд отрицательный. Тогда, учитывая, что поток вектора положительный, а
заряд отрицательный:
∫∫ (P,dS ) = ∫∫ σ′dS = −q′ .
S S
Это теорема Гаусса для вектора поляризованности в интегральном виде. Соответственно, в
дифференциальном виде:
divP = −ρ′ .
Запишем теорему Гаусса для электростатического поля внутри диэлектрика
divE = ρСТОР + ρ′ . ε0
(здесь указано, что электрическое поле создается сторонними зарядами с объемной плотностью
ρ и связанными зарядами с объемной плотностью ρ′).
div (ε0 E ) = ρСТОР + ρ′ = ρСТОР − divP ,
3
|
|
|
|
|
Семестр 3. Лекция 4. |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
div (ε0 E + P ) = ρСТОР . |
|
|||
|
Вектор |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D = ε0 E + P |
|
|||
называется вектором электрического смещения или вектором электрической индукции. Следо- |
|||||||||
вательно, из теоремы Гаусса для вектора электрической напряженности следует теорема Гаусса |
|||||||||
для вектора электрического смещения |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
divD = ρСТОР . |
|
|||
Это теорема Гаусса для электрического поля в веществе (в дифференциальной форме). |
|||||||||
|
В интегральной форме: поток вектора электрического смещения через любую замкну- |
||||||||
тую поверхность, ориентированную наружу, равен алгебраической сумме сторонних зарядов, |
|||||||||
охватываемых этой поверхностью. |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫∫ (D,dS ) = q . |
|
|||
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В однородном, изотропном диэлектрике P = æε0 E , поэтому |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D = ε0 E + æε0 E = (æ +1) ε0 E |
|
||||
Если обозначить ε=æ+1 – (относительную) диэлектрическую проницаемость вещества, то для |
|||||||||
вектора смещения внутри однородного изотропного диэлектрика |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D = εε0 E . |
|
|||
Замечание. Для вакуума ε=1 (нет вещества, поэтому æ=0). Для воздуха при условиях незначи- |
|||||||||
тельно отличающихся от нормальных тоже ε≈1. |
|
|
|
||||||
|
|
|
Поле на границе раздела диэлектриков. |
|
|||||
|
|
|
|
|
|
|
|
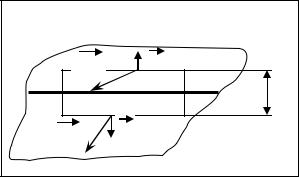
Рассмотрим поле на плоской границе разде- |
|
|
|
L |
|
|
|
ла (в случае неплоской границы достаточно рас- |
|||
|
|
|
|
|
|
||||
|
A |
dl |
D |
1 |
|
смотреть малый участок). |
|
||
|
E1 |
|
|
|
Воспользуемся теоремой о циркуляции вектора |
||||
|
|
|
C |
|
h |
||||
|
B |
dl |
|
|
напряженности в интегральном виде |
||||
|
E2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
∫ (E ,dl ) = 0 . |
||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
L |
|
В качестве контура интегрирования выберем прямоугольник ABCD размером L×h, располо- |
|||||||||
женный таким образом, что одна сторона DA находится в первом диэлектрике, вторая BC – во |
|||||||||
втором, а граница делит прямоугольник пополам. |
|
|
|||||||
|
|
|
|
|
|
∫ (E ,dl ) = |
∫ (E ,dl ) + ∫ |
(E ,dl ) + ∫ |
(E ,dl ) + ∫ |
(E ,dl ) = 0 |
|
L |
DA |
AB |
BC |
CD |
|
4
|
|
|
|
|
|
|
Семестр 3. Лекция 4. |
|
|
|
|
||
При устремлении h→0 последние два интеграла стремятся к нулю. |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Но (E ,dl ) = Et dl , где Et – касательная составляющая вектора напряженности. |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Поэтому ∫ (E ,dl ) |
≈ ∫ (E ,dl ) + |
∫ (E ,dl ) = E1t L − E2t L = 0 . |
|
|
|
||||||||
|
L |
|
DA |
|
|
AB |
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
Окончательно, E1t |
= E2t |
- на границе раздела ди- |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
электриков величина касательной составляющей |
|||||
|
D1 |
|
n |
|
1 |
|
|
вектора напряженности электрического поля не |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
меняется. |
|
|
|
|
|
|
D2 |
n |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
Теперь применим теорему Гаусса в веществе. |
||||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫∫ (D,dS ) = q . |
||
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
В качестве поверхности интегрирования выберем прямой цилиндр высотой h, основания кото- |
|||||||||||||
рого (площадью S каждое) параллельны границе раздела. Пусть граница раздела делит пополам |
|||||||||||||
цилиндр. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫∫ (D,dS ) = ∫∫ |
(D,dS ) + ∫∫ |
(D,dS ) + ∫∫ |
(D,dS ) = q |
|||||||
|
|
|
S |
|
|
S1ОСН |
|
S2 ОСН |
|
SБОК |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Учтем, что(D,dS ) |
= (D,n ) dS = D dS , |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
где Dn – нормальная составляющая вектора смещения. |
|
|
|
|
|||||||||
Если высота цилиндра стремится к нулю h→0, интеграл по боковой поверхности цилиндра |
|||||||||||||
стремится к нулю, поэтому |
|
|
|
|
|
|
|
|
|
||||
|
|
|
∫∫ (D,dS ) + |
∫∫ (D,dS ) ≈ −D1n S + D2n S |
|
S1ОСН |
S2ОСН |
|
В пределе, получаем |
|
|
|
D2n − D1n |
= σ . |
Изменение величины нормальной составляющей вектора смещения на границе раздела диэлек-
триков равно плотности стороннего заряда на границе.
Если на границе нет сторонних зарядов (σ=0), то нормальная составляющая вектора смещения не меняется: D2n = D1n
Если рассмотреть теорему Гаусса для вектора поляризованности в интегральной форме
∫∫ (P,dS ) = −q′
S
то можно, по аналогии, записать
P |
− P |
= −σ′ . |
2n |
1n |
|
5
|
|
Семестр 3. Лекция 4. |
|
||
Изменение величины нормальной составляющей вектора поляризованности равно с обратным |
|||||
знаком поверхностной плотности связанного заряда. |
|
||||
|
|
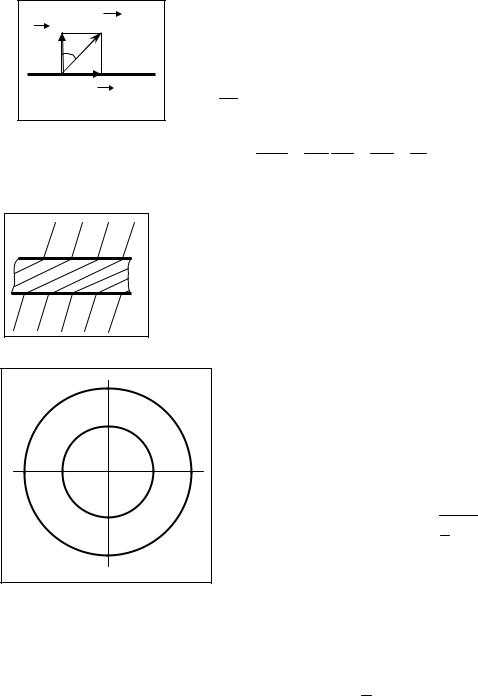
Соотношения на границе диэлектрика (при отсутствии сторонних заря- |
|||
En |
E |
дов) можно переписать в виде ε2 E2n = ε1E1n , E1t = E2t .Если ввести угол |
|||
α |
отклонения силовой линии от нормали к границе диэлектрика |
||||
|
|
||||
|
Et |
tgα = Et , то для углов по разные стороны от границы |
|||
|
En |
|
|
|
|
|
|
|
|
|
|
|
|
tgα2 = E2t E1n = E1n = ε2 . |
|||
|
|
tgα1 |
E2n E1t |
E2n |
ε1 |
|
|
При ε2>ε1 получаем α2>α1 – в диэлектрике с большей относительной про- |
|||
|
|
ницаемостью силовые линии больше отклоняются от вертикального на- |
|||
|
|
правления. |
|
|
|
|
|
Т.е. в диэлектрике силовые линии электрического поля сгущаются. Гово- |
|||
|
|
рят, то диэлектрик «накапливает силовые линии». |
|||
Пример.Рассмотрим поле внутри и снаружи равномерно заря-
женного шара. Диэлектрическая проницаемость внутри постоян-
на и равна ε>1. Вне шара ε=1.
Пусть заряд шара q>0, а радиус R, тогда объемная плотность за-
ряда
q
ρ = 4 πR3 . 3
Задача имеет сферическую симметрию.
При r<R в качестве поверхности интегрирования возьмем концентрическую сферу меньшего радиуса. Поверхность ориентирована наружу. Вектор смещения и нормаль в каждой точке па-
раллельны друг другу. По теореме Гаусса
D4πr 2 = ρ 4 πr3
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
||
Поэтому при r<R получаем величина смещения |
D = |
ρ |
r , откуда для напряжённости |
E1 |
= |
D1 |
||||||||||
3 |
εε0 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
E1 = |
ρ |
|
|
r |
= |
|
|
q |
|
|
r . |
|
|
|
||
|
|
|
|
|
|
|
|
|||||||||
3εε |
0 |
4πεε |
R3 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
||
Снаружи при r>R напряжённость поля E2 = |
|
|
q |
|
|
. |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||||||||
4πε |
r 2 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
6
Семестр 3. Лекция 4.
Видно, что на границе раздела величина вектора напряженности терпит разрыв при r=R:
E1 = |
q |
|
|
< E2 = |
q |
|
. |
|
|
|
|
|
|||
4πεε |
0 |
R2 |
4πε |
R2 |
|||
|
|
|
|
0 |
|
|
Этот разрыв вызван наличием на поверхности диэлектрика связанных зарядов.
На границе шара сохраняется нормальная составляющая вектора смещения D2n = D1n :
действительно, вектор D направлен по радиусу, поэтому его нормальная составляющая равна
величине вектора Dn |
= D . Но на границе шара |
D1 = D2 |
= |
|
|
|
q |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
4πR2 |
|||||||||||||||||||||||||||||||||||||||||||
Величина поляризованности внутри шара |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
P = æ ε E = (ε −1)ε E = (ε − |
1)ε |
|
|
|
q |
|
|
|
|
|
r = |
(ε1 −1) |
|
q |
|
r |
|
|
|
|
|
|
||||||||||||||||||||||
0 4πε ε |
|
R3 |
|
4πε R3 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
1 |
1 0 1 |
|
1 |
|
0 1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Вне шара величина вектора поляризованности (ε2=1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
P = æ |
2 |
ε |
E = |
(ε |
2 |
−1) |
ε |
E = 0 . |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
0 |
|
2 |
|
|
|
|
|
|
|
|
|
0 |
|
|
2 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вектор внутри шара P направлен по радиусу (т.к. он направлен также как E ), поэтому его нор- |
||||||||||||||||||||||||||||||||||||||||||||
мальная составляющая равна величине вектора P = P . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Поэтому на границе должно выполняться: −P = −σ′ , откуда плотность связанных зарядов на |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
поверхности шара: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
σ′ = (ε1 −1)ε0 E1 = (ε1 −1)ε0 |
|
|
|
|
|
q |
|
|
|
|
|
|
|
= |
q (ε1 −1) |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
4πεε |
0 |
R2 |
4πε R2 |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|||||
Поверхностный связанный заряд q′ |
|
= σ′S = |
q (ε1 −1) |
|
4πR2 |
= |
|
q (ε1 −1) |
. |
|||||||||||||||||||||||||||||||||||
|
4πε R2 |
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ПОВ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ε |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из теоремы Гаусса |
divP = −ρ′ для вектора поляризованности найдём объёмную плотность свя- |
|||||||||||||||||||||||||||||||||||||||||||
занного заряда. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
dP |
|
|
|
|
|
|
|
|
|
|
|
|||||
Для сферически симметричного случая divP = |
2 |
|
|
+ |
|
|
|
|
, |
поэтому |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
dr |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
P dP |
|
|
(ε −1) |
|
q |
|
|
(ε −1) |
|
q |
|
|
|
|
( |
ε −1) q |
|||||||||||||||||||||||||
ρ′ = − |
2 |
1 |
+ |
1 |
= − 2 |
1 |
|
|
+ |
1 |
|
|
|
|
|
|
|
|
= −3 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
R3 |
|
|
|
|
|
|
R3 |
|
|
|
|
|
|
|
|
|
R3 |
|||||||||||||||||||||||
|
|
|
r dr |
|
4πε1 |
|
|
|
4πε1 |
|
|
|
|
|
|
|
|
|
|
4πε1 |
|
|||||||||||||||||||||||
Откуда связанный заряд внутри шара q′ |
= ρ′V |
|
= −3 (ε1 −1) |
q |
4 |
πR3 = − (ε1 −1) q . |
||
|
R3 |
|
|
|||||
ВНУТР |
|
ВНУТР |
4πε |
3 |
ε |
|||
|
|
|
|
1 |
|
|
|
1 |
Общий связанный заряд всего шара q′ = q′ |
|
+ q′ |
= 0 .♣ |
|
|
|
|
|
ВНУТР |
ПОВ |
|
|
|
|
|
|
|
7
