Глава 3. Металлоконструкция

3.1. Расчет балки

Конструкция сварной балки пролетом l=32 м. Балка нагружена равномерной нагрузкой от собственного веса q=0,35 Т/м и двумя сосредоточенными грузами Р=3,5 Т (от веса тележки с грузом), которые могут перемещаться по балке.

Расстояние между осями тележки d=1,8 м; материал – сталь Ст. 3; допускаемое напряжение [σ]_р=16 кГ/мм². Наибольший прогиб балки f от сосредоточенных грузов не должен превышать 1/500 ее пролета.

Конструирование балки следует начать с определения расчетных усилий М и Q.

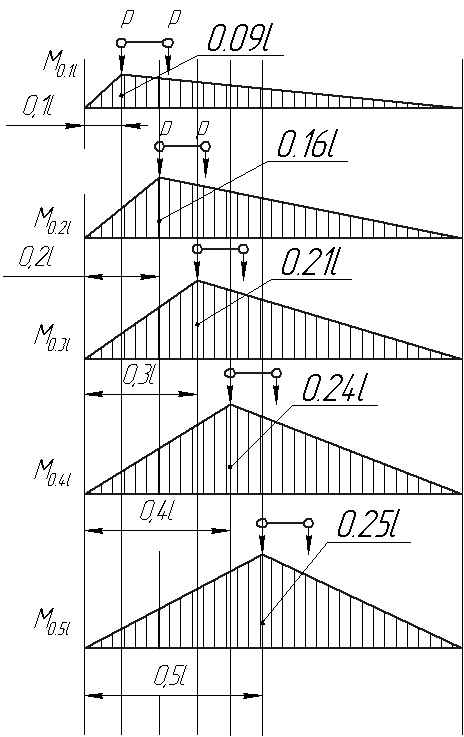
1. Построим линии влияния моментов, чтобы знать их максимально возможные значения в разных сечениях балки.

В сечении Ордината линии влияния

0,1l M=0,09l=0,09·32=2,88

0,2l M=0,16l=0,16·32=5,12

0,3l M=0,21l=0,21·32=6,72

0,4l M=0,24l=0,24·32=7,68

0,5l M=0,25l=0,25·32=8,00

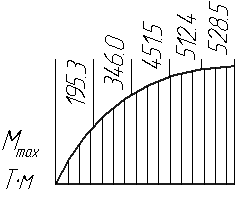
2. Величина изгибающего момента от сосредоточенных сил:

где у_i – ордината линии влияния;

Р – величина сосредоточенного груза.

В сечении при l=32 м и d=1.8 м

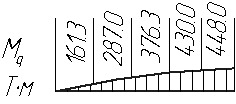
3. Определим изгибающие моменты от равномерно распределенной нагрузки:

В сечениях

4. Вычислим суммарные величины моментов в сечениях от сосредоточенных сил и равномерной нагрузки:

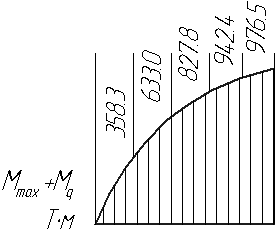
Таким образом, расчетной величиной момента для балки является М=97.65 Тм=976500 Нм.

5. Требуемый момент сопротивления балки для этого усилия равен:

6. Производим построение линии влияния поперечной силы:

в сечении х=0, ордината линии влияния Q₀=1;

в сечении х=0.1l, ордината линии влияния Q₀=0.9;

в сечении х=0.2l, ордината линии влияния Q₀=0.8

в сечении х=0.3l, ордината линии влияния Q₀=0.7;

в сечении х=0.4l, ордината линии влияния Q₀=0.6;

в сечении х=0.5l, ордината линии влияния Q₀=0.5;

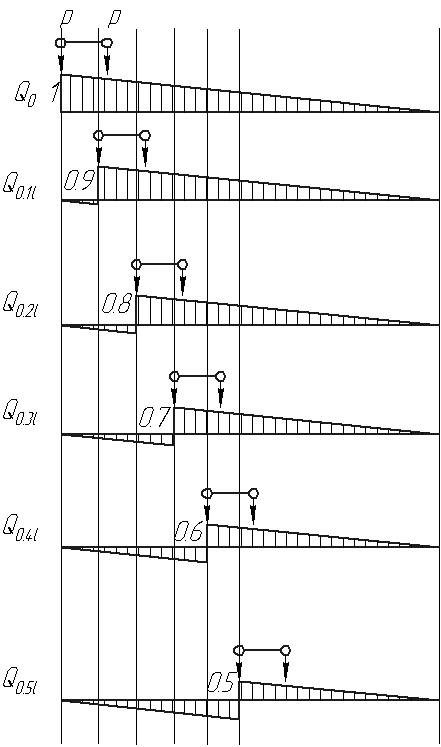
7. Определим расчетные усилия от сосредоточенных сил в каждом из указанных сечений того, что одна из них располагается над вершиной линии влияния:

В сечении х=0 при l=32 м и d=1.8 м

В сечении х=0.1l

В сечении х=0.2l

В сечении х=0.3l

В сечении х=0.4l

В сечении х=0.5l

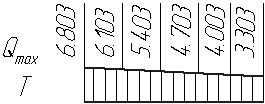
8. Поперечные силы Q от собственного веса q равны;

9. Расчетные значения поперечных сил от сосредоточенных и равномерно распределенных нагрузок:

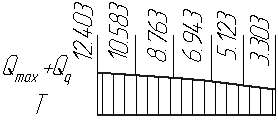
10. Требуемая высота балки из условий жесткости:

При этом h=0.053·3200=85.33 см.

11. Толщина вертикального листа:

Примем S_в=8 мм.

12. Требуемая высота из условия наименьшего веса.

[12, c.311]

Принимаем высоту балки h=175 см

Высота вертикального листа h_в=173 см

13. Момент инерции поперечного сечения сварной балки:

[12, c.311]

14. Момент инерции подобранного вертикального листа 1730×8 мм:

[12, c.312]

15. Требуемый момент инерции горизонтальных листов балки (поясов):

16. Сечение одного пояса балки:

[12, c.312]

17. Уточненное значение момента инерции подобранного поперечного сечения балки:

18. Наибольшее нормальное напряжение в крайнем волокне балки:

[12, c.313]

18. Касательное напряжение на уровне центра тяжести балки в опорном ее сечении:

[12, c.313]

где Q=12403 кГ – расчетная поперечная сила;

S – статический момент половины площади сечения относительно центра тяжести балки.

18. Эквивалентное напряжение:

[12, c.313]

где σ₁ – нормальное напряжение от М;

τ₁ – касательное напряжение от Q;

где S=12.5·1·87=1087.5 – статический момент площади сечения горизонтального листа относительно центра тяжести;

отсюда

18. Вычислим функцию α:

где b – ширина пояса;

s_Г – толщина горизонтального листа;

l₀= 10÷20=1245 см – расстояние между закреплениями.

Зная функцию α по графику [12, с.315] определяем коэффициент ψ=1.73

18. Момент инерции балки:

18. Найдем коэффициент φ:

устойчивость обеспечена

18. Устойчивость вертикального листа:

Привариваем к листу ребра жесткости. Расстояние между ними

Среднее касательное напряжение от поперечной силы:

18. Местное напряжение под сосредоточенной силой:

где z – условная длина, на которой сосредоточенный груз распределяется в вертикальном листе;

где J_П – момент инерции верхнего пояса с приваренным к нему рельсом;

где J^/_П - момент инерции относительно оси а;

у – ордината центра тяжести сечения пояса и рельса;

18. Проверим правильность постановки ребер жесткости:

а)

б)

где ν – отношение большей стороны к меньшей; в принятой конструкции а/h_в=1.5;

d – наименьшая из сторон пластин (а или h_в), заключенных между поясами и ребрами жесткости; В данном случае d=h_в=173 см;

в)

По графику определяем К₁=8.6 [12, с.318]

18. Местная устойчивость вертикального листа:

18. Устойчивость в опорных сечениях:

на опоре σ₁=0

на опоре σ=0

Устойчивость обеспечена.