
Дополнительные главы математики.-2
.pdf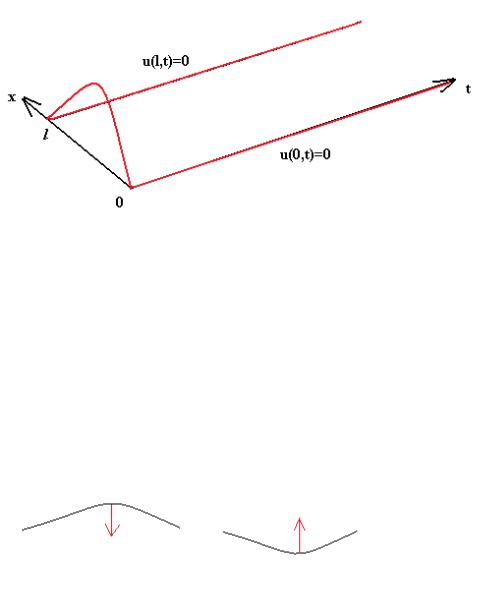
Уравнение теплопроводности (диффузии).
Теперь рассмотрим другой процесс. Пусть задан узкий стержень, и
температура в каждой его точке. Либо плотность газа внутри узкой трубки. Как она будет меняться с течением времени? В области высоких температур (или плотности газа), будет происходить их снижение, переток энергии в соседние области. Но в этом случае
именно скорость (а не ускорение по |
t ) |
пропорциональна кривизне |
графика, т.е. второй производной |
по |
x . Чем больше разность |
плотностей, тем больше скорость перераспределения частиц.
61
Уравнение примет вид
u |
|
|
|
2 |
u |
|
a |
2 |
|
f (x,t) |
|||
|
|
|
|
|||
t |
|
x |
2 |
|||
|
|
|
||||
|
|
|
|
|||
, или в других
обозначениях,
u a |
2 |
u |
f |
|
|
|
|
t |
|
xx |
|
. Здесь не 2-я, а 1-я производная по
t
.
Решение |
волнового |
уравнения |
и |
уравнения |
теплопроводности методом Фурье разделения переменных.
Пусть |
u(x, t) |
имеет вид |
X (x)T (t) , |
произведением двух различных функций от |
x и от |
||||||||
|
a |
2 |
|
X (x)T |
|
2 |
X |
|
|
utt |
|
uxx примет вид: |
(t) a |
|
(x)T (t) . |
||||
то есть |
является |
t . Тогда |
уравнение |
Тогда
1 |
T (t) |
|
||
a |
2 |
T (t) |
||
|
||||
|
|
|||
X (x) X (x)
.
Но дву функции, одна от
x
, другая от
t
,
могут быть равны лишь в том случае, когда они обе равны одной и той же константе, иначе противоречие. Обе должны обладать
свойством: |
отношение 2-й |
производной к самой |
функции |
равно |
||
константе. |
Кстати, такие |
функции существуют, |
например, |
e |
kx |
, |
|
||||||
sin( kx)
Итак,
, |
cos(kx) . |
1 |
T (t) |
|
X (x) |
|
||
a |
2 |
T (t) |
X (x) |
|||
|
|
|||||
|
|
|
||||
. Уравнение распадается на 2 различных
уравнения:
X (x)
X (x)
Решим первое из них.
,
1 |
T (t) |
|||
a |
2 |
T (t) |
||
|
||||
X (x) |
|
|||
X (x) |
||||
|
||||
.
X (x) X (x)
0
, это линейное
однородное уравнение, его характеристическое уравнение Возможны 3 случая: 0 , 0 , 0.
r |
2 |
|
0
.
62
|
Рассмотрим |
0 . Тогда характеристическое |
корни |
|
, |
|||||||||
ФСР |
e |
x |
, e |
|
x |
, |
общее решение |
X (x) C1e |
x |
C2e |
|
x |
. |
Но |
|
|
|
|
|
|
|||||||||
теперь применим граничные условия: если концы струны закреплены,
то X (0) X (l) 0 . В этом случае, получается:
X (0) C |
C |
2 |
1 |
|
0
,
X (l) C e |
l |
C |
e |
l |
0 |
|
|
||||
1 |
|
2 |
|
|
|
Тогда система уравнений на C1 |
,C2 |
: |
|
|
|
|
|
|
|
|
|||||||
|
C |
C |
2 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
l |
C |
|
e l |
0 |
|
|
|
|
|
|
|
|
|
|
|
||
C e |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1 |
|
2 |
|
|
|
|
|
|
|
|
C1 e |
|
|
|
0 |
|
|
Из 1-го, |
C2 |
|
C1 |
, тогда C1e |
l |
C1e |
l |
0 |
l |
e |
l |
, |
|||||
|
|
|
|
|
|||||||||||||
но так как выражение в скобках не равно 0 (экспонента в двух разных
точках принимает разные значения), то C1 0 , а значит и C2 |
0 . |
Итак, при 0 возможно только тривиальное решение. |
|
|
|
Рассмотрим случай |
0 |
. Тогда |
X |
(x) 0 |
, общее решение |
X (x) C1 C2 x . Применим
Получим систему уравнений:
граничные
|
|
C |
0 |
|
|
|
1 |
|
|
|
C |
l |
||
C |
||||
|
1 |
|
2 |
|
0
условия
, откуда
X (0)
C |
0 |
1 |
|
,
X (l)
C |
2 |
|
|
|
0 0 .
.
Рассмотрим третий случай: 0.
подчеркнув, что она отрицательна.
уравнение r 2 2 0, корни
Сразу обозначим |
|
2 |
, |
|
|
||||
Тогда |
характеристическое |
|||
i , |
общее |
решение |
||
дифференциального уравнения:
X (x)
C cos( x) C |
2 |
1 |
sin( x)
.
Применим граничные условия X (0) X (l) 0 .
63

|
|
|
|
|
C |
0 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin( l) 0 |
|
|
|
|
|
|
|
|
|
|||
C cos( l) C |
2 |
|
|
|
|
|
|
|
|
|
|||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
C1 |
0 , |
|
C2 sin( l) 0 . При этом |
C2 |
0 |
sin( l) 0 |
l k |
||||||||||||
|
|
k |
|
|
|
|
|
|
|
|
|
|
k |
|
|
||||
|
|
. |
Тогда вид функции: |
X (x) C2 sin |
|
x . |
|
||||||||||||
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Теперь решим уравнение по t , а именно |
1 |
T (t) |
. |
Но при этом |
|||||||||||||||
a |
2 |
T (t) |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
2 |
|
|
k |
|
|
|
|
|
|
|
мы уже знаем, что |
, где . |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
1 |
T (t) |
2 |
|
|
|
T (t) 2 a 2T (t) 0 |
, |
|
характристическое |
||||||||||
a |
2 |
T (t) |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
уравнение
r |
2 |
2 |
a |
2 |
0 |
|
|
|
r
i a
, общее решение
T (t)
C |
3 |
cos(at) C |
4 |
|
|
sin(
at)
,
а учитывая тот факт, что
|
k |
|
l |
||
|
,
получаем
T (t)
C |
|
ka |
|
C |
|
|
3 |
cos |
|
t |
4 |
||
|
|
l |
|
|
||
|
|
|
|
|||
ka |
|
sin |
|
|
l |
t
.
Тогда окончательный
|
k |
|
|
ka |
|
|
вид решения: |
u(x, t) C2 sin |
|
x C3 cos |
|
t |
|
|
|
l |
|
|
l |
|
|
|
|
||||
В |
каждой точке |
x (0, l) |
происходят |
|
сечение |
по t |
синусоида или косинусоида, |
||
График функции |
u(x, t) представлен на чертеже: |
|||
|
ka |
|
|
|
C4 sin |
|
t . |
|
|
l |
|
|
|||
колебания, то есть или их комбинация.
64

Теперь решим уравнение теплопроводности (диффузии) этим
же методом. Пусть
u(x, t)
X
(x)T (t)
. Тогда уравнение
u |
|
|
|
2 |
u |
a |
2 |
|
|||
|
|
|
|
||
t |
|
x |
2 |
||
|
|
||||
|
|
|
|||
примет вид
X (x)T (t) a |
2 |
X (x)T (t) |
|
|
1 |
T (t) |
|
||
a |
2 |
T (t) |
||
|
||||
|
|
|||
X (x) X (x)
. При
этом относительно |
x |
получается точно такое же уравнение, которое |
недавно решали. Мы уже знаем, что 2 , причём lk ,
k |
|
X (x) C sin |
|
|
l |
x
.
А вот в решении уравнения относительно
t
будут существенные отличия, ведь оно не 2-го, а 1-го порядка.
1 T (t) 2 a2 T (t)
T (t) 2 a 2T (t) 0 , его характеристическое
уравнение r 2a2 , общее решение Т (t) Сe 2a2t . Таким образом,
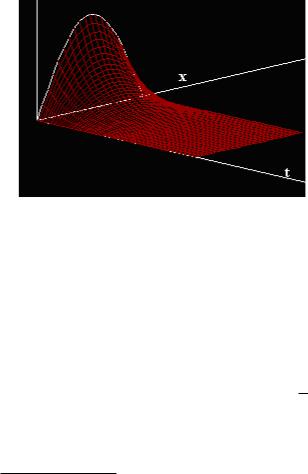
окончательный вид функции u(x, t) :
65
k |
|
|
a |
t |
|
u(x, t) С sin |
|
x e |
2 |
2 |
|
|
|
|
|
||
|
l |
|
|
|
|
В каждом сечении по оси
.
t
, убывающая экспонента.
О приближённых методах решения дифференциальных
уравнений в частных производных.
Чтобы находить приближённые решения с помощью компьютера, необходимо научиться сначала задавать 1-ю и 2-ю
производные.
Пусть дан массив значений u(xi ,0) |
с шагом h , где h |
l |
. |
|
n |
||||
|
|
|
Информацию о первой производной по |
x можно получить, вычислив |
значение:
u(x |
,0) u(x ,0) |
i 1 |
i |
|
h |
. Информация о 2-й производной по
x
может быть получена с помощью значения такого выражения:
|
u(xi 1 ,0) u(xi ,0) |
|
u(xi ,0) u(xi 1 ,0) |
|
|
u(xi 1 ,0) 2u(xi ,0) u(xi 1 |
|
|
|
h |
h |
|
= |
,0) |
. |
||
|
|
|
||||||
|
|
h |
|
|
h2 |
|
||
|
|
|
|
|
|
|
66

При решении уравнения теплопроводности, можно
следующего слоя (при следующем |
t ) получить с помощью |
|
|
u(x |
i 1 |
,0) 2u(x |
,0) |
|
предыдущего слоя, прибавляя величину |
|
|
i |
|
||
|
|
h |
2 |
|
||
|
|
|
|
|
||
|
|
|
|
|
|
|
умноженную на |
t . Однако численные методы выходят |
|||||
нашего курса. |
|
|
|
|
|
|
значения
значений
u(x |
i 1 |
,0) |
, |
|
|
||
|
|
|
за рамки
ЛЕКЦИЯ 7. 07.05.2019
Приведение дифференциального уравнения к каноническому
виду.
Дифференциальное уравнение в частных производных, содержащее функцию от n переменных, может содержать множество смешанных производных. Наиболее общий вид:
n |
n |
|
|
|
2 |
u |
|
|
n |
u |
|
|
|
|
a |
ij |
|
|
|
i |
cu |
f |
|||||
|
|
|
x |
x |
|
b |
x |
|
|||||
i 1 |
j 1 |
|
|
j |
|
i 1 |
i |
|
|
||||
|
|
i |
|
|
|
|
|
|
|||||
.
Возникает вопрос: можно ли свести к виду, содержащему только не смешанные производные 2 порядка, то есть, чтобы для коэффициентов выполнялось равенство aij 0 при i j . На прошлой лекции во всех полученных уравнениях (волновом,
диффузии) не было смешанных производных, и мы изучили метод их решения.
Оказывается, с помощью замены переменных действительно можно
n |
|
2 |
u |
n n |
|
2 |
u |
|
свести к виду, содержащему aij |
|
вместо aij |
|
. |
||||
|
|
|
|
|
|
|||
i 1 |
xi2 |
i 1 j 1 |
xi x j |
|||||
67

Сейчас вам станет понятно, для чего мы ранее в линейной алгебре изучали приведения квадратичных форм к главнм осям. Именно этот алгоритм поможет устранить смешанные производные.
Для каждого дифференциального уравнения можно построить матрицу, состоящую из коэффициентов:
a |
... |
a |
|
|
|
11 |
|
1n |
|
A |
|
|
|
|
|
|
... |
|
|
an1 |
ann |
|||
Если квадратичную форму с такой матрицей привести к главным осям, то после такой замены перемнных исчезнут все вмешанные производные.
Рассмотрим на таком примере. Дано дифференциальное уравнение
2
0
|
2 |
u |
|
|||
|
|
|
||||
|
|
|
|
|
||
x y |
||||||
|
2 |
u |
|
|||
|
|
1 |
||||
x |
2 |
|||||
|
||||||
|
|
|
||||
0 . Это же можно записать в виде: |
|||||||||||||
|
2 |
u |
|
|
2 |
u |
|
|
2 |
u |
|
|
|
|
1 |
|
0 |
|
0 |
. Мы специально распределили |
|||||||
x y |
y x |
y |
2 |
||||||||||
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
поровну коэффициенты между двумя смешанными производными
2u 2u
x y , y x , чтобы получилась симметричная матрица. Это можно
сделать, так как они совпадаюти между собой. Матрица: |
0 |
|
A |
|
|
|
|
1 |
|
|
|
Найдём собственные числа и собственные векторы линейного оператора, соответствующего этой матрице.
1 |
|
|
|
0 |
|
|
|
.
68
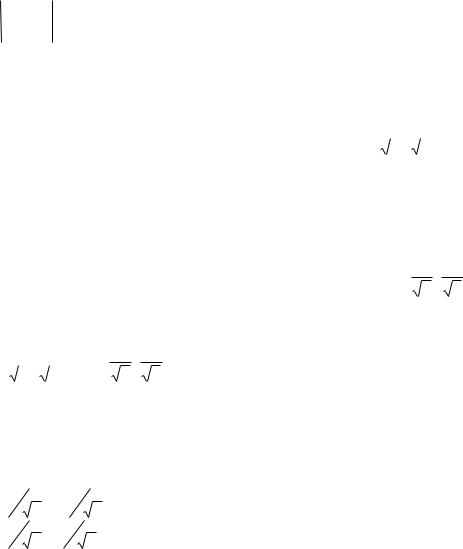
1 0
1
2 |
1 0 |
|
1
собственные числа.
При
1
: решаем однородную систему
1 |
|
|
|
|
1 |
|
|
1 a |
||
|
|
|
1 |
|
|
b |
||
|
0 |
|
|
|
|
|
0 |
|
|
|
|
,
a b , то есть вектор
(1,1)
|
1 |
|
|
1 |
|
|
||
. Нормируем его, получаем |
|
|
|
, |
|
|
|
. |
|
|
|
|
|
|
|||
|
|
|
|
|||||
|
2 |
|
|
2 |
|
|
||
1 |
1 a |
|
|
0 |
||||
При 1: решаем однородную систему |
|
|
|
|
|
|
|
|
|
1 |
1 |
|
b |
|
|
|
0 |
|
|
|
|
|
||||
|
|
|
|
|
||||
a b , то есть вектор ( 1,1) . Нормируем его, получаем |
|
|
||||||
|
||||||||
|
|
|
|
|
|
|
|
|
Новый ортонормированный базис состит из пары векторов
|
, |
|
|
|
|
|
|
1 |
|
|
2 |
, |
1 |
|
2 |
||
|
.
|
1 |
|
|
1 |
|
|
|
|
1 |
|
1 |
|
|
||
|
|
|
|
, |
|
|
|
|
и |
|
, |
|
|
. Фактически, это повёрнутый |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
||||||||||
|
2 |
|
|
2 |
|
|
|
|
2 |
|
2 |
|
|
||
декартов базис (1,0) и (0,1).
Вспомним о том, что взаимосвязь между старыми (x, y)
коодинатами (z, w) такова:
на 900
и новыми
|
1 |
|
1 |
|
|
x |
|
|
2 |
|
2 |
z |
|||
|
|
|
|
|
|
||
1 |
|
1 |
|
|
|
|
|
|
|
w |
y |
||||
|
2 |
|
2 |
|
|
|
|
В матрице перехода векторы нового базиса расположены по векторам.
Таким образом,
69
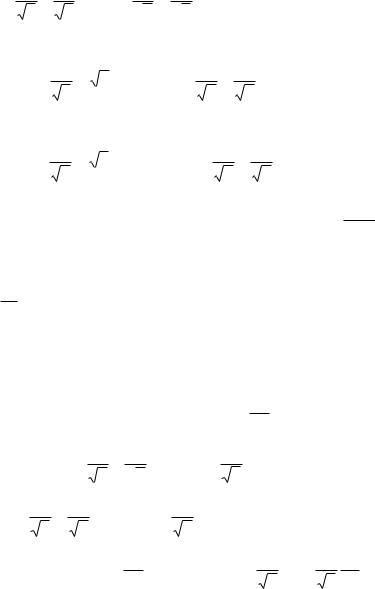
x |
z |
|
w |
|
2 |
2 |
|||
|
|
и
y
z 
 2
2
w 
 2
2
.
Если сложить эти 2 равенства, получим:
x y 2 |
z |
|
2z , тогда z |
x |
|
y |
. |
|
|
2 |
2 |
2 |
|
||||||
|
|
|
|
|
|
||||
Аналогично, вычитая 1-е из 2-го, получим: |
|||||||||
y x 2 |
w |
|
2w , тогда w |
x |
|
y |
. |
||
2 |
2 |
2 |
|||||||
|
|
|
|
|
|
||||
Теперь пересчитаем смешанную |
производную |
||||||||
|
|
2 |
u |
|
2 |
|
|||
x y |
||||
|
||||
по формуле
полной производной. Изначально можно её записать в виде:
2 |
|
|
u |
|
|
|
|
|
y |
x |
|
представив дифференцирование по x, y как два
последовательных действия. По формуле полной производной, если переменные z, w рассматриваются как промежуточные:
При этом, z |
x |
|
||||
2 |
||||||
|
|
|
|
|
||
w |
x |
|
y |
|
||
2 |
2 |
|||||
|
|
|
|
|||
Тогда |
u |
|
u z |
|
||
x |
z x |
|||||
|
|
|
||||
y 
 2
2
wx
uw
u |
|
u |
||
x |
z |
|||
|
||||
|
z |
|
||
x |
||||
|
|
|||
|
1 |
. |
|
|
2 |
|
|||
|
|
|
||
w |
|
|
|
|
x |
|
|
||
|
|
|
||
z |
|
u w |
|
x |
w x |
||
|
|||
1 |
, |
|
|
|
|
||
2 |
|
||
u |
|
1 |
u |
|
x |
2 |
z |
||
|
.
|
1 |
|
2 |
||
|
uw
.
Теперь применим к этой функции дифференцирование по y таким же
образом.
70
