Эксперимент №1. Моделирование усилительного звена

Дифференциальное уравнение звена с учетом (10) имеет вид: .

Используя (12), получим выражение для выходной переменной . Введём обозначения:, гдеК – коэффициент усиления.

Передаточная функция системы будет иметь вид .

Рис 2.1. Структурная схема

Порядок выполнения эксперимента:

1. На блоке Step установить время приложения сигнала «0».

2. В теории управления на осциллографе обычно регистрируются входной и выходной сигналы, для того чтобы можно было увидеть изменение входного сигнала при прохождении его через систему. Для получения входного сигнала на осциллографе необходимо сигнал с блока Step подать на один из входов блока Mux и далее на Scope.

3. Для получения выходного сигнала необходимо соединить последовательно блоки Step, Gain, Mux, Scope.

4. Исследуйте изменение выходного сигнала при изменении коэффициента усиления. Коэффициент на блоке Gain может задаваться одним значением или в виде набора коэффициентов (в квадратных скобках через пробел).

5. Получить модель усилительного звена с использованием блока Transfer Fcn, для этого необходимо открыть блок и установить коэффициенты числителя и знаменателя передаточной функции.

6. Добавить на блоке Mux ещё один вход и подключить блок Transfer Fcn к набранной схеме.

7. Схему моделирования и графики сохранить в отчёте.

Внимание.

При выполнении последующих экспериментов полученную схему моделирования не разбирать, скопировать её и внести в неё необходимые изменения.

Эксперимент №2. Моделирование интегрирующего звена Дифференциальное уравнение звена с учетом (10) имеет вид: .

Используя (12), получим выражение для старшей производной выходной переменной .

Введём обозначения: ,тогда передаточная функция имеет вид: .

Рис. 2.2. Структурная схема

Порядок выполнения эксперимента:

1. Скопировать схему из первого эксперимента и добавить блок Integrator после блока Gain.

2. Исследуйте изменение выходного сигнала при изменении коэффициента усиления.

3. Получить и исследовать модель интегрирующее звено с использованием блока Transfer Fcn.

4. Подайте на вход интегратора синусоидальный сигнал и исследуйте реакцию системы.

5. Схему моделирования и графики сохранить в отчёте.

Эксперимент №3 Моделирование апериодического звена первого порядка.

Дифференциальное уравнение звена с учетом (10) имеет вид:

Используя (12), получим выражение для старшей производной выходной переменной

Рис. 2.3.1. Структурная схема апериодического звена.

Приведём дифференциальное уравнение к стандартной форме .

Введём обозначения: ,. Операторная передаточная функция имеет вид, где К – коэффициент усиления звена, Т – постоянная времени звена.

Для получения модели используем внутренний сумматор и единичную обратную связь.

Рис. 2.3.2.Схема набора апериодического звена с использованием

внутреннего сумматора

В общем случае набранная структура соответствует звену с передаточной функцией (при получении передаточной функции использовать материал о типовых соединениях звеньев):

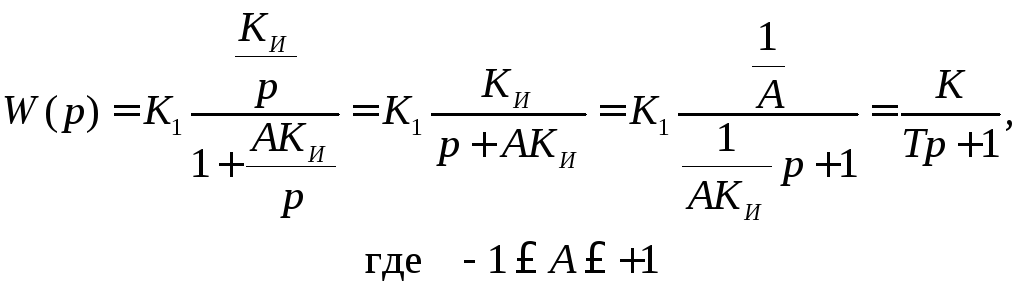
Порядок выполнения эксперимента:

1. Скопируйте схему интегрирующего звена, добавьте в неё после первого коэффициента усиления () сумматор (+ -), ещё один коэффициент усиления ()перед интегратором. Охватить интегратор и усилитель единичной отрицательной обратной связью ().

2. Исследуйте изменение выходного сигнала при изменении сначала коэффициента при постоянстве, потом при постоянстве .

3. Получить модель апериодического звена с использованием блока Transfer Fcn.

Возможен другой вариант моделирования апериодического звена первого порядка с использованием внешнего сумматора.

Рис. 2.3.3. Схема набора апериодического звена с использованием

внешнего сумматора