
- •М.А. Шварц
- •Конспект лекций
- •23.05.05 «Системы обеспечения движения поездов»
- •Раздел 8. Дифференциальные уравнения Санкт-Петербург 2020 Тема 1
- •1. Дифференциальные уравнения первого порядка
- •Метод Эйлера приближенного решения задачи Коши
- •Тема 2 Уравнения с разделяющимися переменными
- •Однородные уравнения
- •Тема 3 Линейные дифференциальные уравнения
- •Уравнение Бернулли
- •Уравнения в полных дифференциалах
- •Тема 4 дифференциальные уравнения высших порядков
- •Понижение порядка уравнения
- •Тема 5 Линейные дифференциальные уравнения высших порядков
- •Тема 6 Линейные однородные уравнения с постоянными коэффициентами
- •Линейные неоднородные уравнения с постоянными коэффициентами. Метод Лагранжа
- •Темы 7,8 Линейные неоднородные уравнения с постоянными коэффициентами. Метод неопределенных коэффициентов
- •Контрольные тесты
- •Тема 9 системы дифференциальных уравнений
- •Системы линейных уравнений с постоянными коэффициентами
- •Решение однородных систем линейных уравнений
- •Контрольные тесты
- •Тема 10 Оригиналы и изображения
- •Теоремы операционного исчисления
- •Изображения основных функций
- •Тема 11 Решение дифференциальных уравнений
- •Решение систем уравнений
- •2 Контрольные тесты
Контрольные тесты
№ |
Задание |
Ответ |
1 |
Порядок
дифференциального уравнения
|
|
2 |
Количество
произвольных постоянных в общем
решение дифференциального уравнения
|
|
3 |
Общее
решение дифференциального уравнения
1)
3)
|
|
4 |
Порядок дифференциального уравнения можно понизить заменой
1)
|
|
5 |
Порядок
дифференциального уравнения
1)
3)
|
|
6 |
Дифференциальному
уравнению
1) k2 + k + 1 = 0 2) k2 + 5 k + 6 = 0 3) 6k2 + 5 k + 1 = 0 4) 6k2 + k + 6 = 0 |
|
7 |
Установите соответствие между дифференциальным уравнением и его характеристическим уравнением:
1) 5y + 4y – 3y = 0 A) 52 – 3 = 0 B) 42 – 3 = 0 2) 5y – 3y = 0 C) 52 + 4 = 0 D) 42 – 3 = 0 3) 5y + 4y = 0 E) 52 + 4 – 3= 0 |
|
8 |
Линейно зависимыми являются функции
1) х3 2) х2 3) х 4) 2х |
|
9 |
Линейно зависимыми являются функции
1)
|
|
10 |
Фундаментальную
систему решений д.у.
1)
3)
|
|
11 |
Общим
решением линейного дифференциального
уравнения с постоянными коэффициентами
и корнями характеристического уравнения
1)
2)
3)
4)
|
|
12 |
Установите соответствие между дифференциальным уравнением и общим видом его частного решения
1)
B)
2)
D)
3)
|
|
13 |
Частное
решение уравнения
1)
3)
|
|
14 |
Частное
решение д.у.
1)
3)
|
|
15 |
Установите соответствие между дифференциальным уравнением и общим видом его частного решения
1)
B)
2)
D)
3)
|
|
16 |
Установите соответствие между дифференциальным уравнением и общим видом его частного решения
1)
B)
2)
D)
3)
|
|

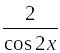 4)
4)

 A)
A)


 C)
C)


 E)
E)

 следует искать в виде
следует искать в виде следует искать в виде
следует искать в виде A)
A)


 C)
C)


 E)
E)

 A)
A)


 C)
C)


 E)
E)
