Тема 6 Линейные однородные уравнения с постоянными коэффициентами

Линейное однородное уравнение второго порядка с постоянными коэффициентами имеет вид у + ру¢ + qу = 0, (р, qR). Подставив в уравнение , , , получим . Учитывая, что при любых х, имеем . Последнее алгебраическое уравнение называется характеристическим. Его корни вычисляются по формуле Возможны три случая.

1. Корни характеристического уравнения вещественные различные: Два частных решения: , образуют фундаментальную систему, т.к. они линейно независимы: .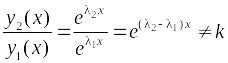

Общее решение дифференциального уравнения: .

2. Корни характеристического уравнения вещественные равные (кратные):

Общее решение: .

3. Корни характеристического уравнения комплексные сопряжённые:

Общее решение д.у.: .

Для линейного однородного д.у. п-го порядка

составляется характеристическое уравнение

.

Соответствие между корнями характеристического уравнения и частными решениями, образующими фундаментальную систему приведено в таблице 2.

Таблица 2

Корни характеристического уравнения	Частные решения
Простой вещественный корень, 
Вещественный корень кратности r,	,
Пара простых комплексных сопряжённых корней,	,
Пара комплексных сопряжённых корней кратности r, …=	, , , , . . . ,

Пример. Найти общее решение уравнения .

Корни характеристического уравнения : . Общее решение: .

Пример. Найти общее решение уравнения .

Корни характеристического уравнения : .

Общее решение: .

Пример. Найти общее решение уравнения .

Корни характеристического уравнения : .

Общее решение: .

Пример. Записать линейное однородное дифференциальное уравнение, общим решением которого является функция .

Корни характеристического уравнения: ₁ = 0, ₂ = –4.

Характеристическое уравнение: ( – ₁) ( – ₂) = 0 или ² + 4 = 0.

Линейное однородное дифференциальное уравнение: у² + 4у¢ = 0.

Пример. Для дифференциального уравнения y^IV + y¢¢¢ + 4y¢ + y = 0 составить характеристическое уравнение.

Характеристическое уравнение: ⁴ +³+4 + 1 = 0.

Пример. Найти общее решение уравнения .

Характеристическое уравнение: .

Корни характеристического уравнения: ₁ = –1, .

Общее решение д.у.: .

Пример. Найти общее решение уравнения .

Характеристическое уравнение: .

Корни характеристического уравнения: , .

Общее решение уравнения:

Пример. Доказать, что при комплексных корнях характеристического уравнения функции и образуют фундаментальную систему.

Два частных решения д.у. при комплексных корнях:

,

.

Линейные комбинации , :

и .

– образуют фундаментальную систему решений.

Пример. Доказать, что при кратных корнях характеристического уравнения функции и образуют фундаментальную систему.

При одинаковых корнях характеристического уравнения Одно частное решение имеет вид . Второе частное решение ищется в виде . Подставив в уравнение у – 2ру¢ + qу = 0 функции , , , получим

Второе и третье слагаемые в скобках обращаются в ноль, т.к.  – корень уравнения и . Любое частное решение уравнения задает функцию , например, . – функции и образуют фундаментальную систему.