Тема 11 Решение дифференциальных уравнений
Применение операционного метода рассмотрим на примере решения линейного дифференциального уравнения второго порядка с постоянными коэффциентами y'' + a1y' + a2y = f(t), при начальных условиях y(0) = y0, y'(0) = y1.
Полагая, что решение уравнения y(t) и функция f(t) являются оригиналами с изображеними Y(p) → y(t), F(p) → f(t) и учитывая что y'(t) pY(p) – y0, y''(t) p2Y(p) – py0 – y1, изображение исходного дифференциального уравнения имеет вид
p2Y(p) – py0– y1 + a1(pY(p) – y0) + a2Y(p) = F(p).
После решения этого операторного уравнения относительно изображения Y(p) определяется оригинал y(t), который является частным решением дифференциального уравнения.
Замечание. Для нахождения общего решения дифференциального уравнения достаточно задать начальные условия в виде произвольных постоянных.
Пример. Найти решение уравнения y'' – 2y' – 8y = et, удовлетворяющее начальным условиям y(0) = 0, y'(0) =0.
Изображение
правой части уравнения: e
t ← 
;
изображение искомого решения: y(t) ← Y(p);
изображения производных: y'(t) pY(p), y''(t) p2Y(p);
операторное уравнение: p2Y(p) – 2pY(p) – 8Y(p) = .
Решение
операторного уравнения: Y(p)
=
;
Разложение фнуции Y(p) на сумму элементарных дробей:
.
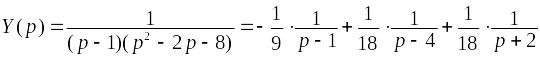Частное
решение д.у.:
Пример. Найти общее решение уравнения y' – 2y = e t.
Назначим начальное условие: y(0) = с.
Изображение правой части уравнения: e t ;
изображение искомого решения: y(t) Y(p);
изображения производной: y'(t) pY(p) – с;
операторное уравнение: pY(p) – с– 2Y(p) = .
Решение
операторного уравнения: Y(p)
=
;
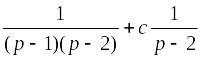разложение Y(p) на сумму элементарных дробей:
,
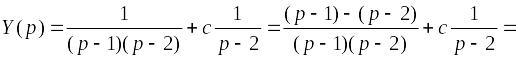
где С
= с
+ 1.
Общее
решение д.у.:
Решение систем уравнений
Применение
операционного метода рассмотрим на
примере решения системы линейных
дифференциальных уравнения второго
порядка с постоянными коэффициентами
при начальных условиях y(0) = y0,
х(0)
= х0.
Полагая, что функции х(t), y(t), f1(t), f2(t) являются оригиналами с изображеними Х(p) → х(t), Y(p) → y(t), F1(p) → f1(t), F2(p) → f2(t) и учитывая, что х'(t) pХ(p) – х0, y'(t) pY(p) – y0, можно записать изображение исходной системы дифференциальных уравнений
После решения полученной алгебраической системы относительно изображений Х(p), Y(p) определяются оригиналы х(t), y(t), которые являются частным решением системы дифференциальных уравнений.
Пример.
Найти частное
решение системы
при начальных условиях
Частное решение системы: x(t) и у(t);
изображения
решения:
,
;
изображения производных:
,
.
Система операторных уравнений:
Решение системы по формулам Крамера:
;
;
;
.
Частное
решение (табл. 1):
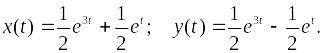
2 Контрольные тесты
№ |
Задание |
Ответ |
1 |
Для оригинала выполняются условия
1) f(t) 0 при t < 0 2) f(t) – непрерывна (либо имеет конечное число разрывов первого рода на любом конечном отрезке) 3) 4) f(t) > 0 |
|
2 |
Оригиналами являются функции
1) |
|
3 |
Изображение функции вычисляется по формуле
1)
3) |
|
4 |
Установите соответствие
1) теорема смещения А) f(t) 2) теорема линейности B) е–tf(t) F(p + ) 3) теорема запаздывания C) f(t – ) e–pF(p) 4) теорема подобия D) с1f1(t) + с2f2(t) с1F1(p) + с2F2(p) |
|
5 |
Функцию
1) 1(t) – 1(t – 1) 2) 1(t) – 1(t – ) 3) 1(t) – 1(t + ) 4) 1(t) + 1(t – ) |
|
6 |
Функцию
1) t1(t) – t1(t – ) 2) t1(t) – 1(t – ) 3) t1(t) – (t – )1(t – ) 4) t1(t) – (t – )1(t) |
|
7 |
Изображение
оригинала
1)
3)
|
|
8 |
Оригинал
изображения равен
1)
|
|
9 |
Оригинал
изображения
1)
3)
|
|
10 |
Установите соответствие между изображениями и их оригиналами
1) А) 2) B) 3) C) 4) D) |
|
11 |
Установите соответствие между оригиналами и их изображениями
1) 1(t) А) 2) B) 3) C)
4)
D)
|
|
12 |
Изображение
оригинала
1)
|
|
13 |
Изображение дифференциального уравнения y' + y = 0 при начальном условии y(0) = 0, имеет вид
1) pY(p) + Y(p) = р 2) pY(p) + Y(p) = 1 3) pY(p) + Y(p) =0 4) Y(p) – p + Y(p) = 0 |
|
14 |
Изображение дифференциального уравнения y'' + y = t при начальных условиях y(0) = 0, y'(0) = 1 имеет вид
1)
p2Y(p)
+ Y(p)
=
3)
p2Y(p)
+ Y(p)
=
|
|
15 |
Изображение
системы дифференциальных уравнений
1)
3)
|
|
16 |
Изображение
полуволны синусоиды
1)
3)
|
|
для всех положительных значений t
2) –t2
3) 
4) 
2) 
4) 
можно
представить в виде
можно
представить
в
виде
равно
2)
4)
2)
3)
4)
равен
2)
4)
равно
2)
3)
4)
2)
p2Y(p)
– 1 + Y(p)
=
4)
p2Y(p)
– p
+
Y(p)
=
при начальных условиях х(0) = 1,
у(0) = 0
имеет вид
2)
4)
имеет вид
2)
4)
