2 / ЦепныеДроби1

6

Задание 1

Задано разложение числа в непрерывную периодическую дробь с периодом 3:

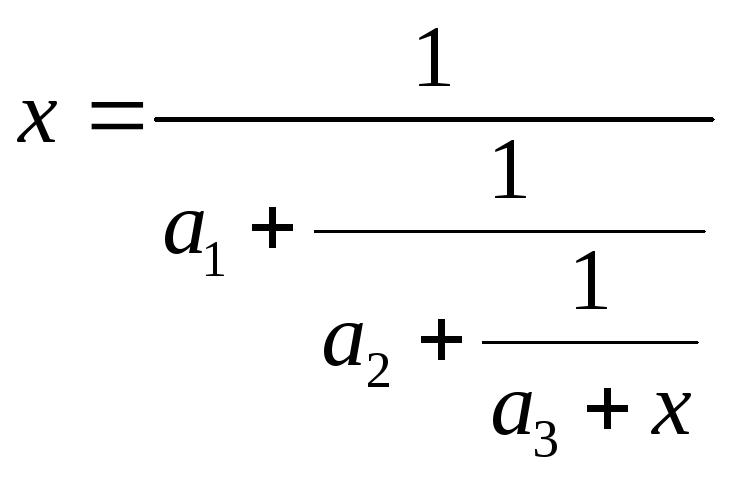(1)

Приведем правую часть этого уравнения к виду обычной дроби:

(2)

Приводя обе части к общему знаменателю, получим квадратное уравнение для :

,

где

Заметим, что дискриминант квадратного уравнения:

.

Поэтому уравнение имеет один положительный и один отрицательный корень. Искомое значение положительно и, следовательно:

Откроем чистый лист Excel и введем в соседние ячейки какой-нибудь строки наименования переменных, например: a_1, a_2, a_3, см. рис. 1.

Пишем так, чтобы избежать совпадений с встроенной адресацией ячеек листа – a1, a2 и т.д. Под каждым именем вводим значение переменной, в нашем случае числа 2, 7, 9.

Ниже располагаем столбиком имена коэффициентов квадратного уравнения, его дискриминанта и корня , а правее каждого имени формулу для его вычисления, причем формулу можно писать, ссылаясь на ячейки листа непосредственно, либо используя имена переменных, предварительно присвоив эти имена ячейкам, где находятся их значения.

Соответствующие записи формулы для коэффициента A будут иметь вид:

=A4*B4+1

=a_1*a_2+1

Запись во второй редакции приближена к обычной математической форме. Имена переменных играют роль абсолютных ссылок.

После того, как все формулы будут введены, в ячейке с формулой для x появится его значение, в нашем случае: 0,467129607.

Введем в ячейку правее x1 формулу =1/($A$4+1/($B$4+1/($C$4+1/B10))), вычисляющую значение x1 по найденному значению x. Данная формула реализует в Excel написанную выше формулу (1) для цепной дроби. Найденное значение x1 = 0,467060885 отличается от предыдущего. Используя формулу (1) вычислим x2 по x1, x3 по x2 и т.д. Формулы для вычисления x2, x3 ,… получим перетаскиванием формулы для x1. Начиная со значения x3, каждое новое значение не отличается от предыдущего. Это значит, что мы нашли значение корня с заданной точностью.

Описанным методом итераций мы можем не только уточнить значение корня, найденное решением квадратного уравнения, но и вычислить его независимо, начиная с какого-нибудь (любого) положительного значения x.

Обоснуем данное утверждение.

Для этого обозначим правую часть уравнения (2) через и выполним некоторые преобразования, чтобы уточнить некоторые свойства этой функции.

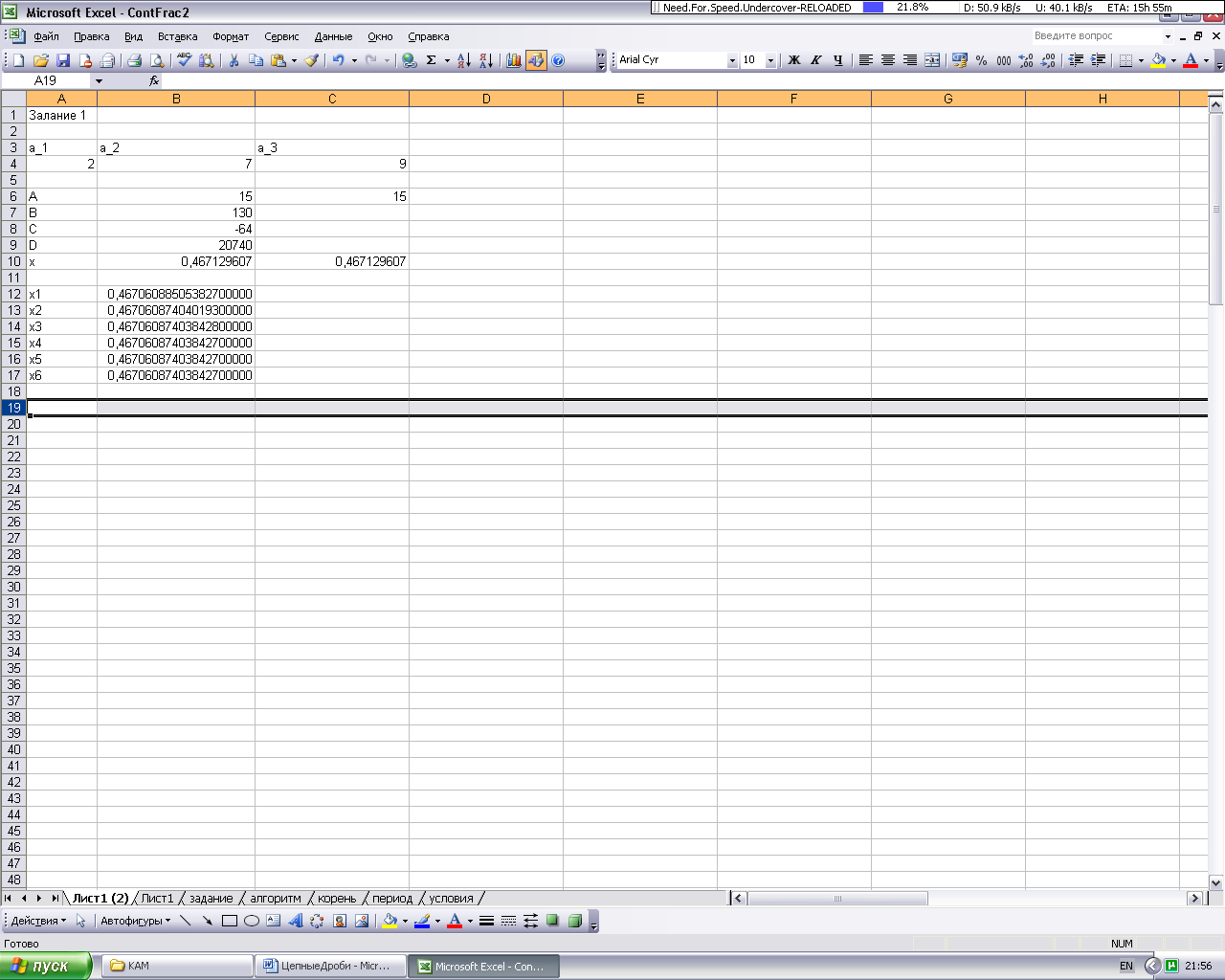
Рис. 1

Именно, выполним тождественные преобразования:

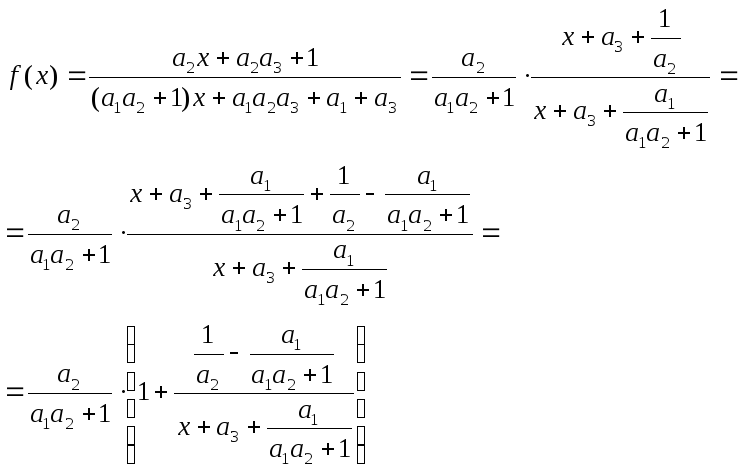
Заметим, что , так как .

Поэтому ,

причем

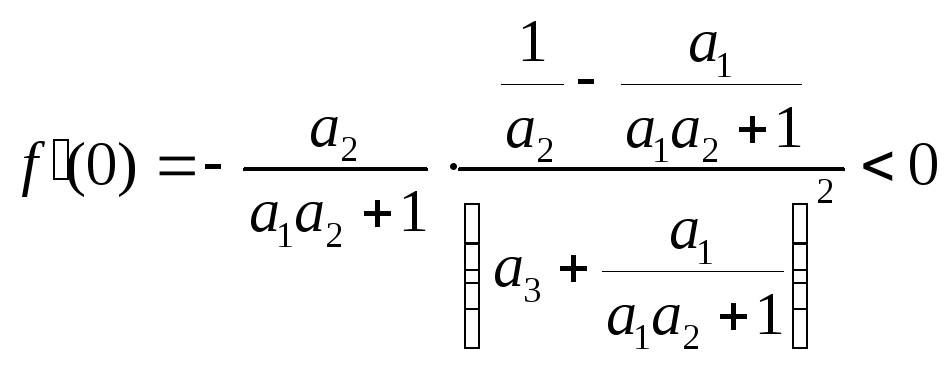
и

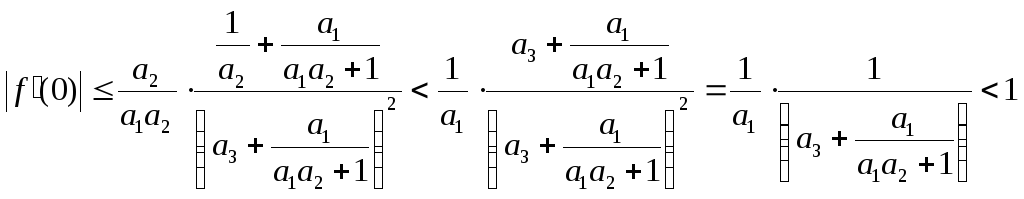
При этом монотонно убывает при изменении от 0 до .

Обозначим через точку пересечения кривой и прямой , т.е. решение нашего уравнения. Проведем через точку прямую , где .

Расположение названных трех линий показано на рис. 2.

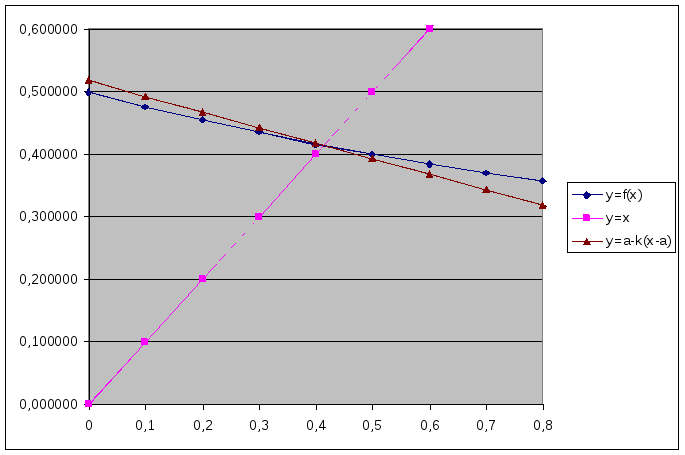
Рис. 2

Видим, что линия расположена между линиями и .

Рассмотрим последовательные итерации на рис. 3.

Возьмем начальное приближение . Пусть , тогда . Из геометрических соображений ясно, что , .

Продолжая далее, получим: . Таким образом, итерационный процесс сходится со скоростью не меньшей, чем геометрическая прогрессия со знаменателем .

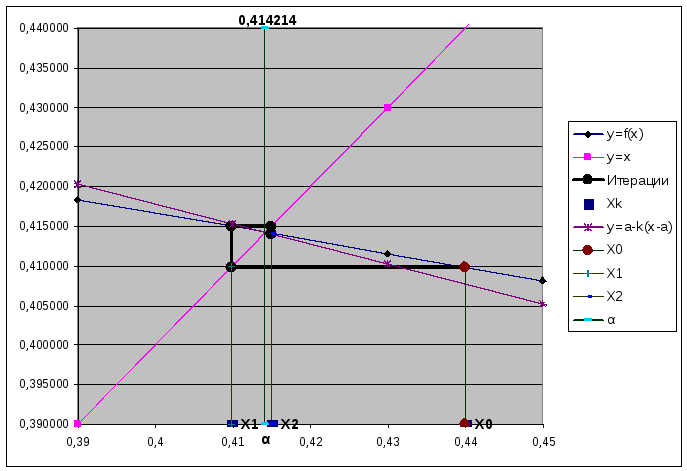
Рис. 3

Для цепных дробей вида (1) линия по существу представляет собой прямую линию, параллельную оси Ох (рис. 4). Поэтому сходимость итерационного процесса очень велика и составляет считанное число итераций.

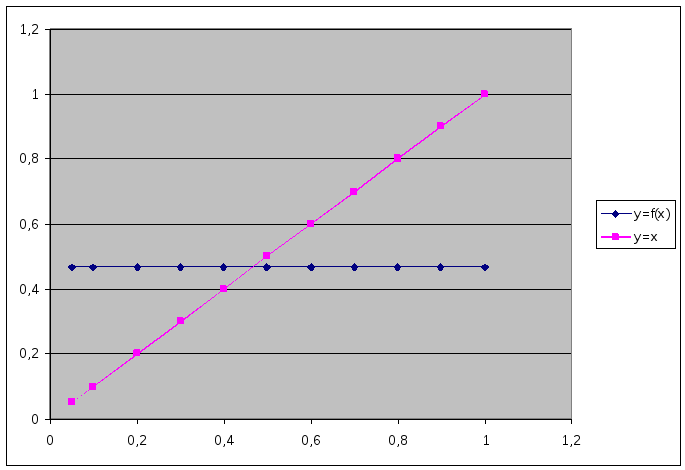
Рис. 4

Задание 2

Дано целое число . Требуется построить разложение в цепную дробь числа :

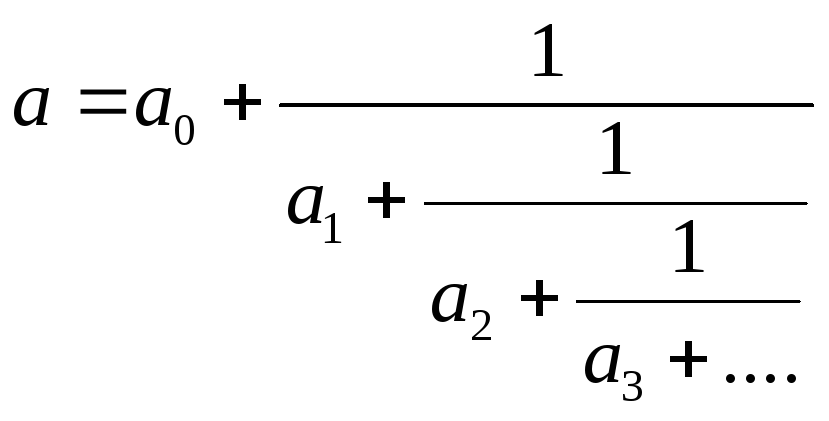
Из теории цепных дробей известно, что такая дробь является периодической:

,

так что нашей задачей является найти повторяющуюся последовательность целых чисел .

Откроем чистый лист Excel и введем в первом столбце наименования A и A^1/2 для значений заданного целого числа и корня из него соответственно, рис. 5. Условимся, что это будут имена ячеек, расположенных справа от них. Введем в ячейку A произвольное целое число, например, 3. В ячейку A^1/2 введем формулу =КОРЕНЬ(B1).

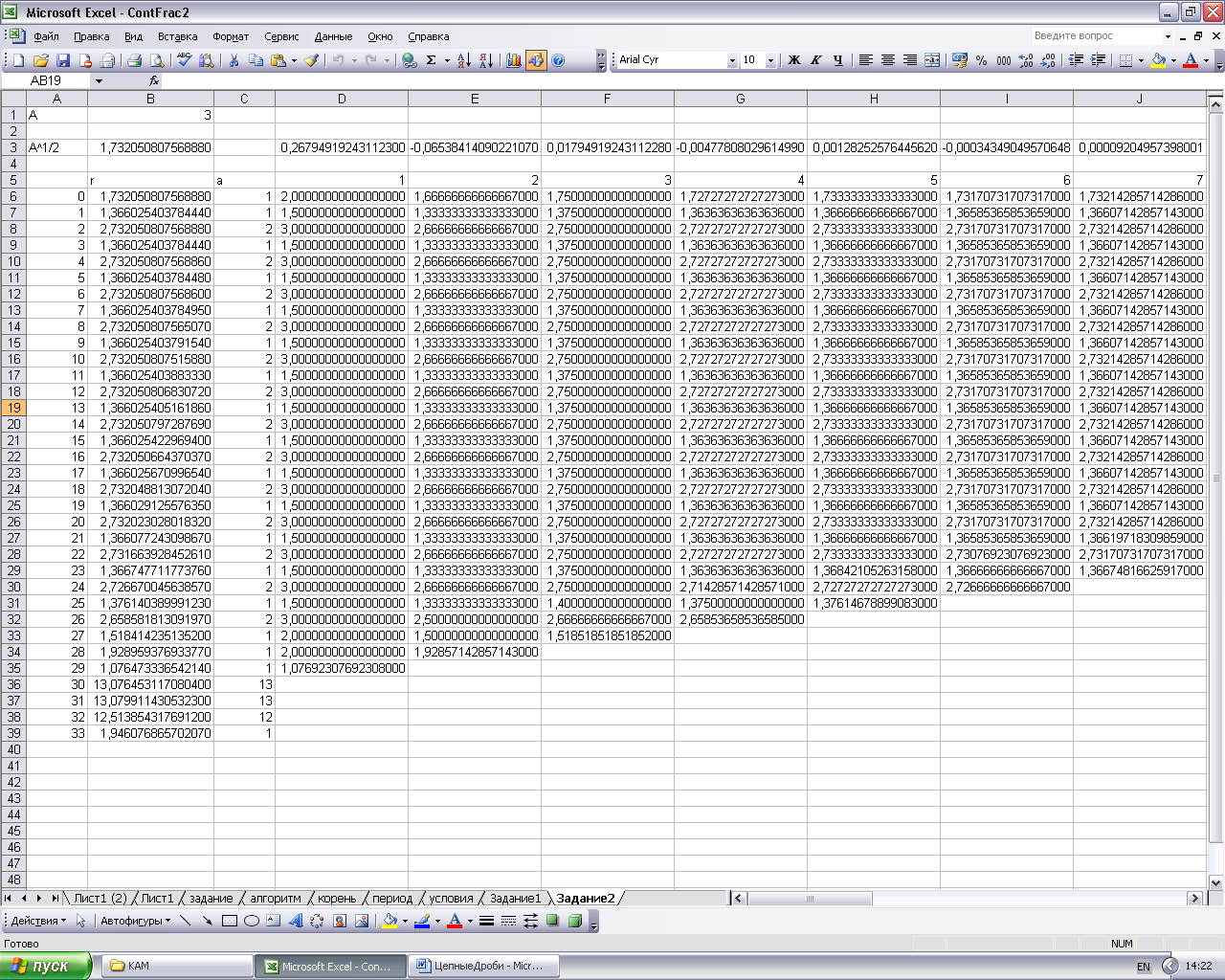Рис. 5.

Ниже будет располагаться таблица вычислений чисел , которая состоит из двух столбов r и a, слева от которых указаны номера последовательных итераций: 0,1,2,…

Условимся при описании ссылаться на ячейки таблицы вычислений, называя имя столбца и номер итерации.

В ячейку r0 введем ссылку на ячейку A^1/2: =B3. В ячейку a0 введем функцию, вычисляющую целую часть значения r0 и выдающую значение END, если r0 уже есть целое число: =ЕСЛИ(ЦЕЛОЕ(B6)=B6;"END";ЦЕЛОЕ(B6)). Значение END означает конец вычислений.

В ячейку r1 вводим формулу, вычисляющую число 1/(r0-a0), а в ячейку a1 формулу для целой части из этого числа, копируя функцию для a0. Формулы для ячеек ri и ai получаем перетаскиванием формул для r1 и a1.

Количество строк в таблице вычислений делаем порядка 30. Этого достаточно, чтобы выявить период цепной дроби. Большее число строк бесполезно, так как из-за накапливающихся погрешностей вычислений, связанных с делением на малые числа, цикл начинает разваливаться, и периодическая закономерность исчезает.

Справа от столбца a построена таблица для вычисления подходящих дробей. Номера столбцов этой таблицы соответствуют порядку подходящей дроби. Строится эта таблица следующим образом. В первую ячейку столбца 1 вводим формулу: =$C6+1/C7, что означает . Знак $ перед индексом столбца C означает, что при копировании этой формулы значение индекса столбца останется неизменным. Далее эту формулу копируем перетаскиванием вниз по столбцу 1. Затем формулу из первой ячейки столбца 1 копируем (перетаскиванием) в первую ячейку столбца 2. Далее первую формулу столбца 2 копируем перетаскиванием вниз по столбцу 2, не доходя на одну ячейку до конца столбца 1. И так далее для остальных столбцов таблицы. В первой строке получаем значения подходящих дробей соответствующих порядков. Наблюдаем сходимость. Она невысокая и совпадение с числом A^1/2 с точностью до 15 знаков после запятой получаем лишь на 25 итерации.

На уровне формулы A^1/2 над соответствующими столбцами введены формулы, вычисляющие погрешность подходящих дробей.