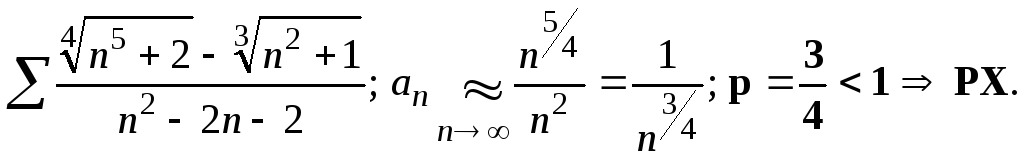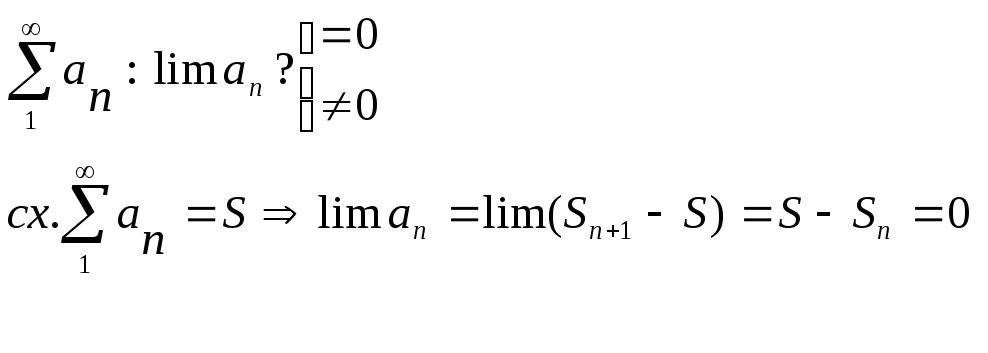8

ГЛАВА «ЧИСЛОВЫЕ РЯДЫ»

Экзаменационные задачи по теме «Ряды».

1. записать ч.ряд, вычислить a₁,a₅, a₁₀; S₁, S₅, S₁₀ с 3 в.з.ц.

§1 Числовой ряд: основные понятия и примеры.

Пусть задана числовая последовательность Определим другую числовая последовательность

Определение 1. Пара числовых последовательностей

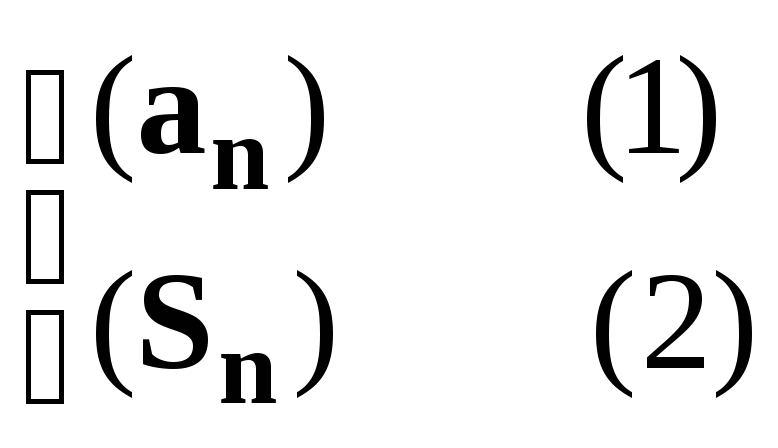
называется числовым рядом, при этом последовательность (1) называется последовательностью членов ряда (a_n – n-ый член ряда), а (2) - последовательностью

частичных сумм ряда ( S_n- n-ая частичная сумма ряда).

 Очевидно, что любая из последовательностей (1), (2) однозначно определяет и другую (т.е. числовой ряд). В дальнейшем выражение будем называть числовым рядом. ------------ЭКЗ-1: записать ч.ряд, вычислить a₁,a₅, a₁₀; S₁, S₅, S₁₀ с 3 в.з.ц. ------------------------------------------ Определение 2. Если существует конечный предел частичных сумм ряда , говорят, что «ряд сходится», этот предел называют «суммой ряда» и пишут . В противном случае говорят, что «ряд расходится» .

Примеры.

1. Геометрическая прогрессия со знаменателем “q”

Известно::



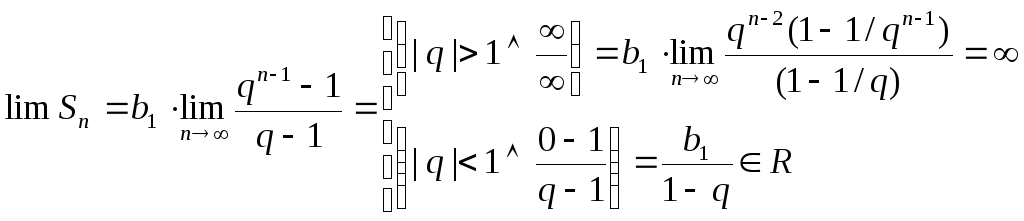
ряд сходится при |q|<1 к сумме ряда S= b1/(1-q) (сумма бесконечно убывающей геометрической прогрессии) и расходится, если |q| > 1.



(2)

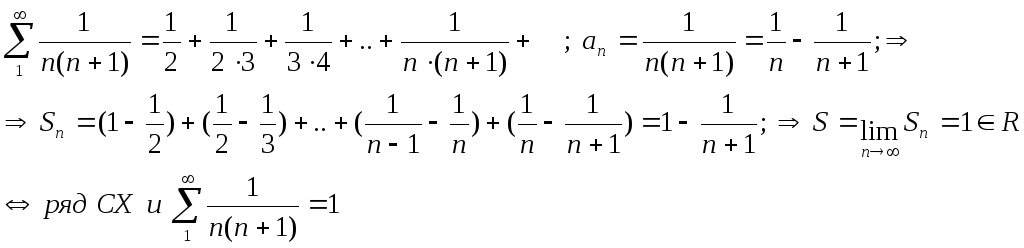
(3)

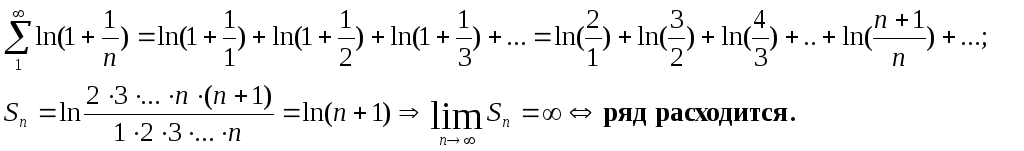
§2 Свойства сходящегося числового ряда.

Из определения сходимости числового ряда и свойств пределов следуют очевидные свойства числовых рядов:

1. 

2. 

3.

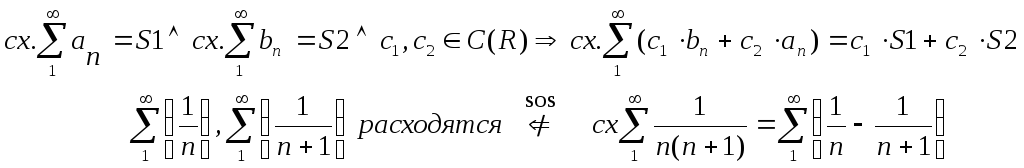
4. 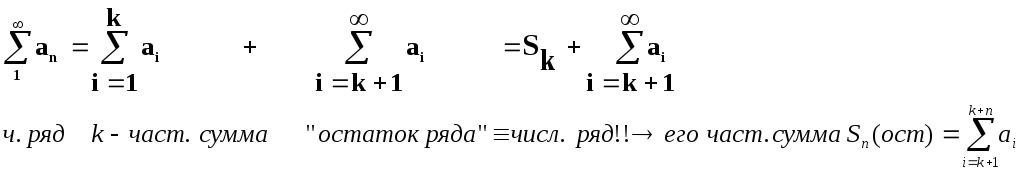Так как

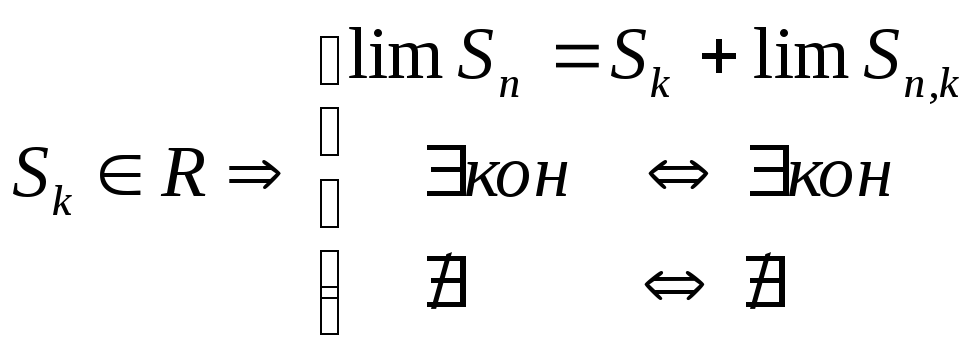
Числовой ряд и «остаток ряда» сходятся и расходятся одновременно.

Следствие. Для сходящегося ряда верно числовое равенство

,

при этом . Следовательно, частичная сумма сходящегося ряда даёт «приближенное значение» суммы ряда

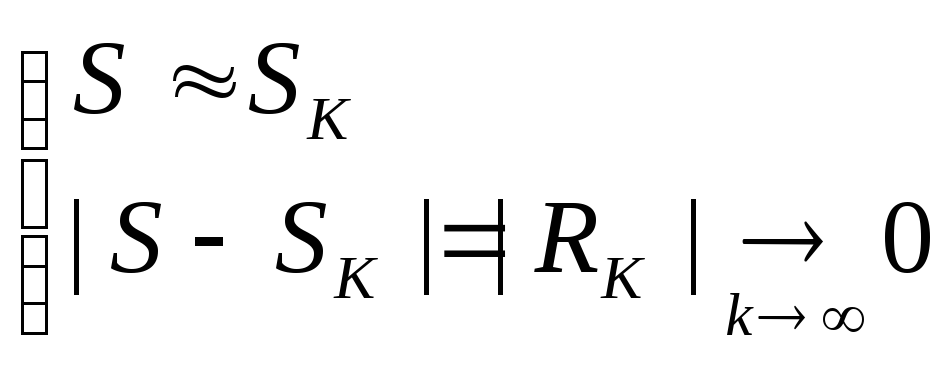
АЛГОРИТМ исследования числового ряда:

[1] исследование сходимости/ расходимости ряда:

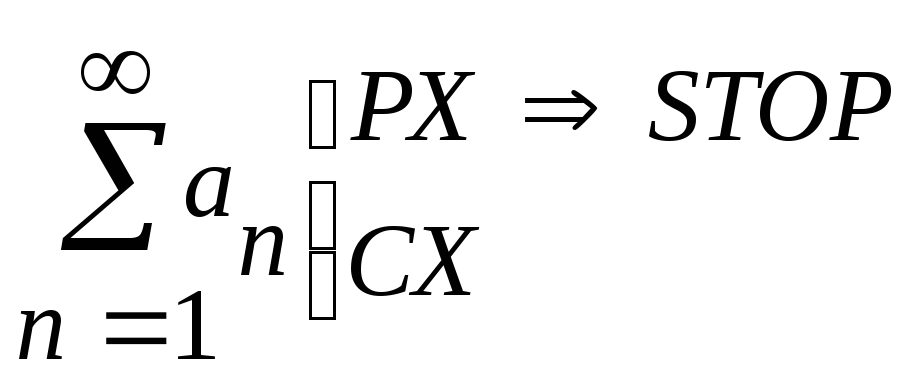
[2] Получение некоторой «оценки» суммы сходящегося ряда.

Задача [1] решается либо «по определению» ,

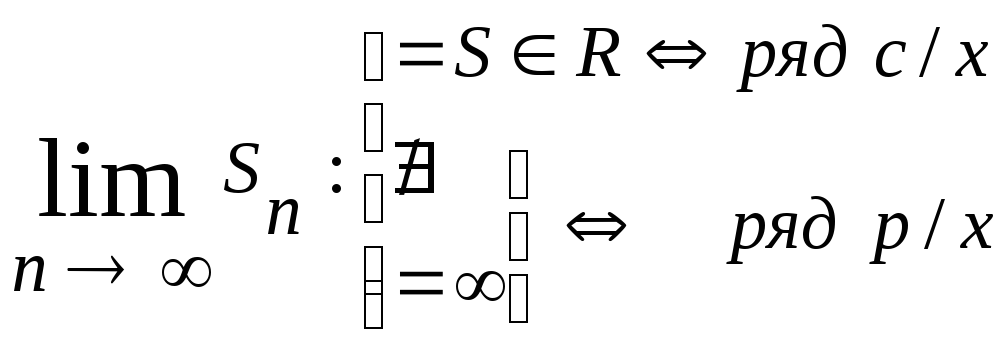либо с помощью «признаков сходимости/расходимости» рядов – теорем, устанавливающих связь между сходимостью/расходимостью ряда и свойствами членов ряда.

Теорема (необходимый признак сходимости и достаточный признак расходимости ч. ряда).

(а) Если числовой ряд сходится, предел модуля его общего члена равен нулю;

(б) если предел модуля общего члена ряда не равен нулю, ряд расходится

Док-во.

(а) Пусть ч.р. сходится ч.т.д.

(б) докажем “методом от противного”. Пусть ??

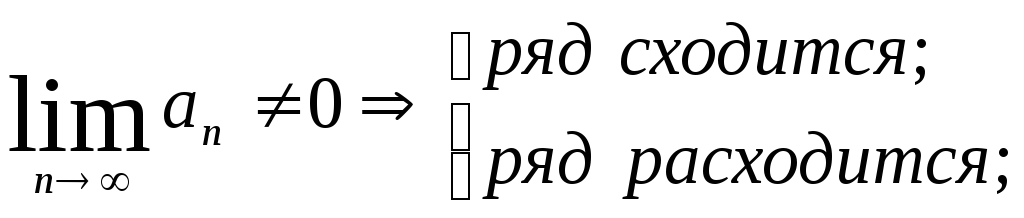Предположим, что ряд сх. (*), , что противоречит условиюпредположение (*) не верно ряд расходится; ч.т.д.





[2] Для получения «оценки» суммы сходящегося числового ряда используется числовое равенство S=S_K+R_K:

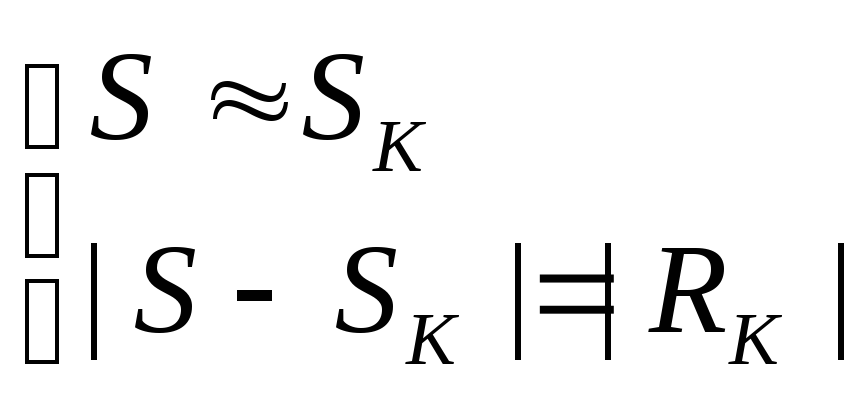
Определение. Если ряд сходится и получена оценка «сверху» суммы его остатка

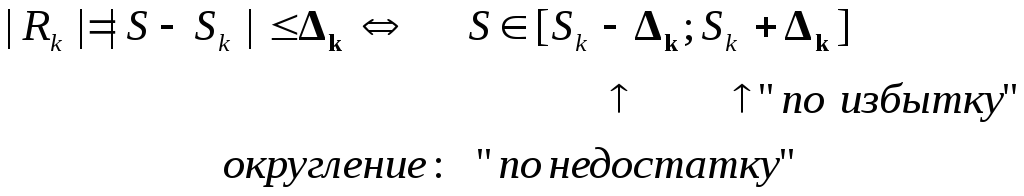
интервал, «накрывающий» сумму ряда S, называют “оценкой суммы ряда с погрешностью 2Δ_К» .

Правила вычислений: 1) Все промежуточные вычисления выполняются в «полной разрядной сетке»: S_K, Δ_K, S_K ± Δ_K 2) Левый конец интервала округляется «по недостатку» , правый – «по избытку»:

§3 Положительные числовые ряды. Интегральный признак сходимости. Интегральная оценка суммы ряда.

Рассмотрим «положительный числовой ряд» . Очевидны

Свойства положительного ряда.

1. Частичные суммы положительного ряда монотонно возрастают

,

3. Известно, что монотонно-возрастающая и ограниченная сверху функция имеет предел.

Следовательно, ряд сходится , если его частичные суммы ограничены СВЕРХУ, т.е. , причем имеют место неравенства

Рассмотрим положительную функцию и ее сужение на множество натуральных чисел N – положительную последовательность и сравним несобственный интеграл и числовой ряд .

По определению сходимости несобственного интеграла и числового ряда

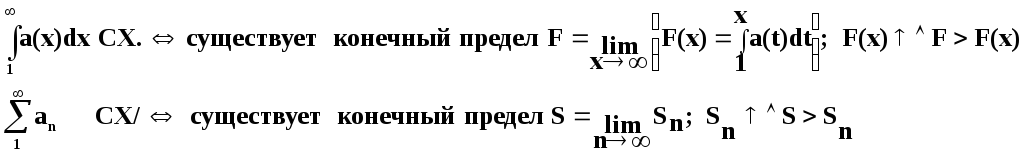
Утверждение (интегральный признак сходимости положительного числового ряда).

Положительный числовой ряд :

(1) сходится и расходится одновременно с несобственным интегралом ,

(2) для сходящегося ряда имеет место

- «интегральная оценка» суммы его остатка и

-.

Следствия.

1. Для сходящегося положительного ряда «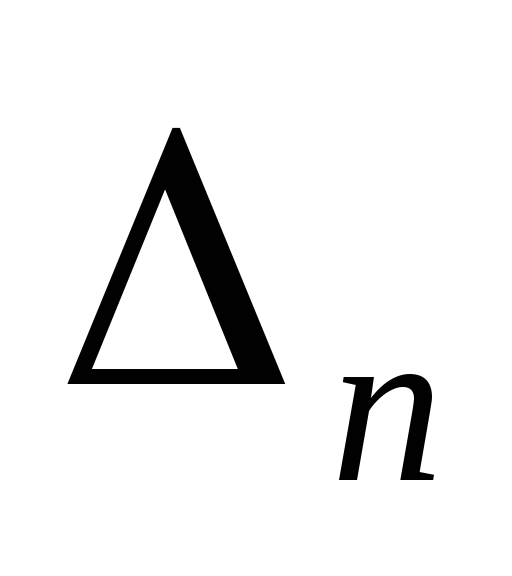-оценка» его суммы имеет вид

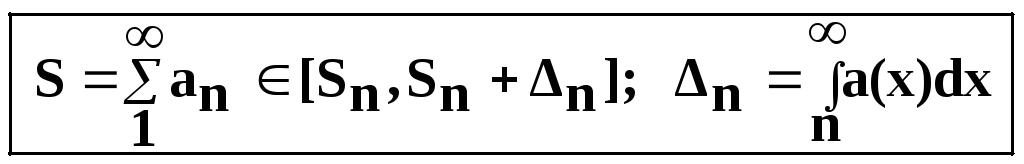
2. Известно,что

Пример . Найти с погрешностью сумму ряда . 

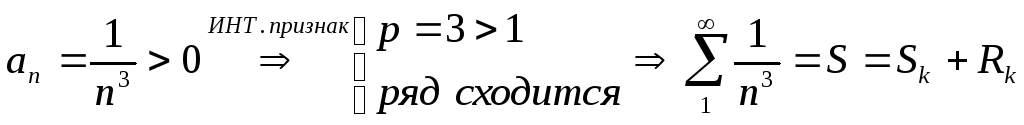
Используя интегральную оценку суммы остатка ряда, решим неравенство

------------------------------------------------

ЭКЗ-2 Найти погрешность приближенной формулы и записать соответствующую оценку суммы ряда . Сравнить полученную оценку с оценкой

. -------------------------------------------

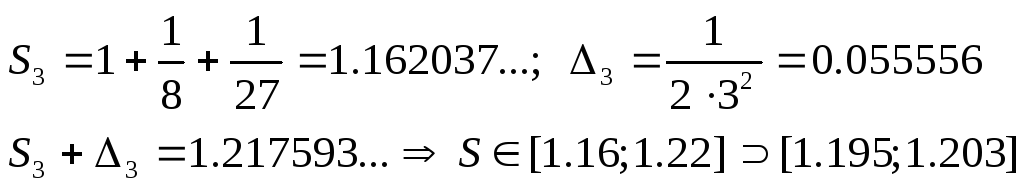§4 Положительные числовые ряды. Признаки сравнения.

Теорема1(признак сравнения). Если , то : (1) из сходимости рядаследует сходимость ряда и (2) из расходимости ряда следует расходимость ряда.

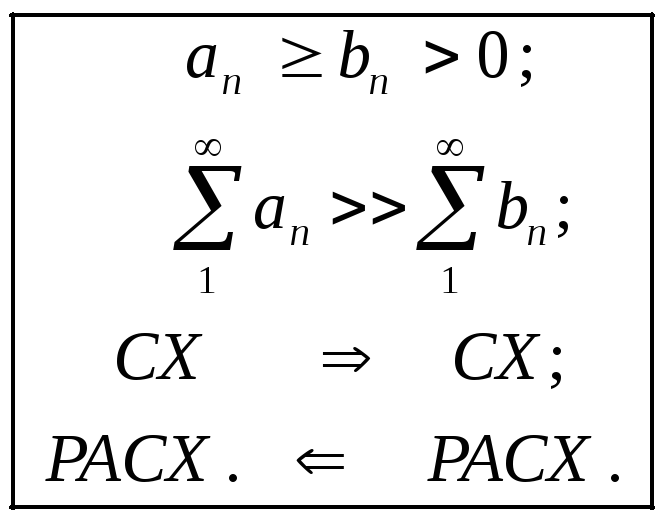
Док-во.

(1) Пусть ряд

2. Доказать самостоятельно методом «от противного».

Пример.

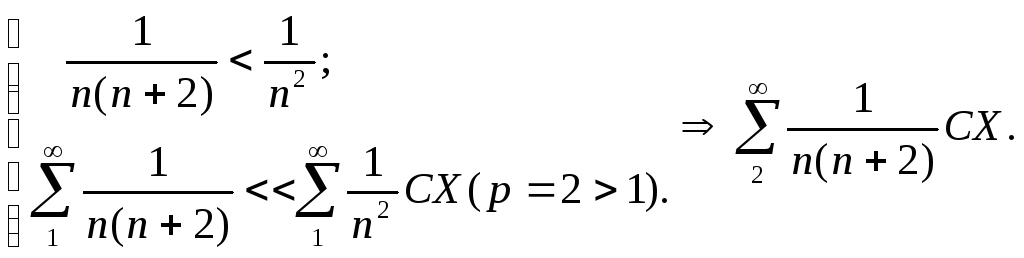
Утверждение 2 (предельный признак сравнения).

Если существует конечный предел отношения членов положительных рядов , ряды сходятся и расходятся одновременно.

------------------------------------------------------------------------

Замечание. Предельный признак сравнения является основным «инструментом» исследования сходимости и расходимости положительных рядов, общий член которых содержит только степенные функции: ;

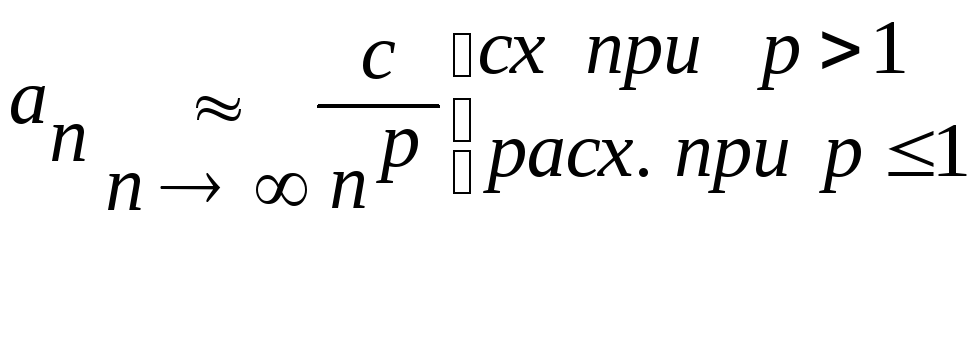(Для установления соотношения равносильности из каждого множителя, представляющего сумму слагаемых, рекомендуется вынести “старшее слагаемое”.)

Примеры.

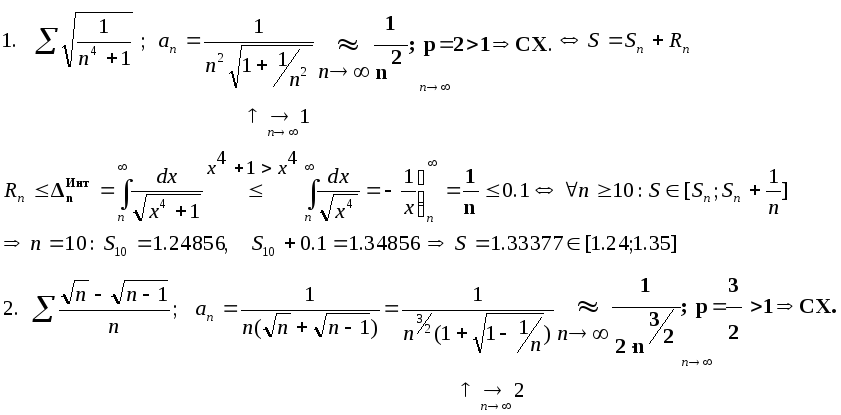
3.