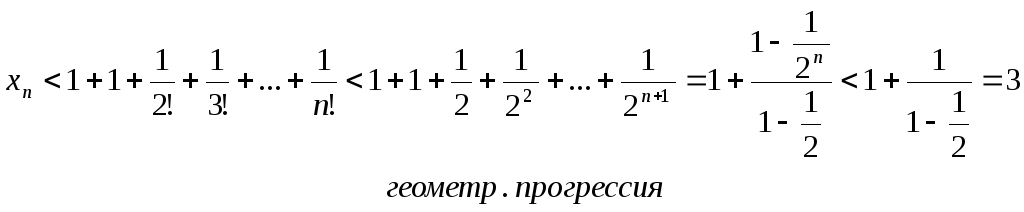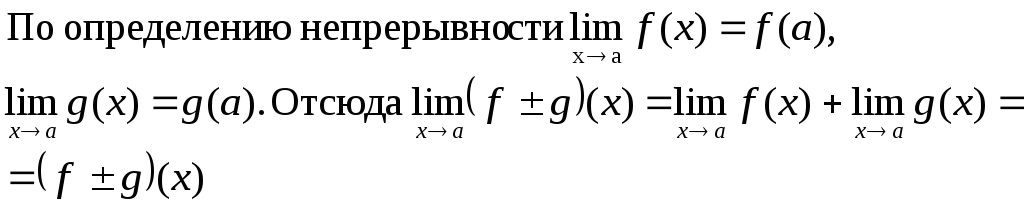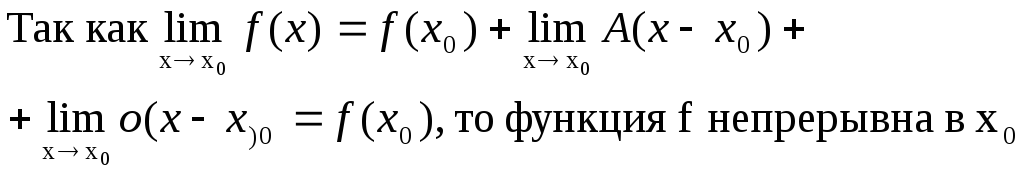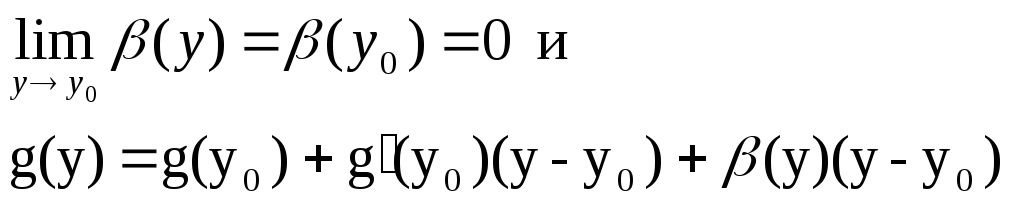3вар.ЛекшнМатан / shpora po Matanu
.doc
|
|
5. Границы числовых множеств. Точная верхняя и нижняя границы. Окрестность точки. Функция. 1) Множество X называют ограниченным сверху, если существует M, для которого x≤M 2) Множество X называется ограниченным снизу, если существует m, для которого m≤x. Множество ограниченное сверху и снизу – ограниченное. Число y называется верхней границей (мажорантой) множества A, если выполняется неравенство x≤y для любого x из А. Число x называется нижней границей (минорантой) множества A, если выполняется неравенство x≤a для любого a из А. Если существует верхняя (нижняя) граница для множества, то все числа, которые больше (меньше) верхней (нижней) границы тоже являются верхними (нижними) границами. Самая маленькая верхняя граница множества называется точной верхней границей – супремумом множества А. Самая большая нижняя граница множества называется точной нижней границей – инфининумом множества А. Окрестность точки: Пусть a,ε принадлежат R, ε>0. Множество:
называется ε-окрестностью точки а. Множество:
назыв. проколотой ε-окрестностью точки а. Функция: Если каждому элементу x принадлежащему X по некоторому правилу f поставлен в соответствие единственный элемент f(x) принадлежащий Y, то говорят, что на множестве X определена (задана) функция f, принимающая значения из множества Y, или, что функция f отображает множество X во множество Y. f: X→Y 6. Предел функции. Бесконечно малые. Теорема о единственности предела и о сохранении знака. Число А называется пределом функции f(x) при ха, если для любого >0 существует такое число >0, что для всех х таких, что 0 < x - a < верно неравенство f(x) - A< .
Функция
f(x)
называется бесконечно
малой при
ха,
где а может быть числом или одной из
величин ,
+
или -,
если.
Бесконечно малой функция может быть только если указать к какому числу стремится аргумент х. При различных значениях а функция может быть бесконечно малой или нет Теорема о единственности предела: (10с.)
|
7. Предельный переход в равенстве и неравенстве. Предельный переход в неравенстве. Если
Д-во: Допустим
противное b>c.
Тогда
Предельный переход в равенстве. Пусть
существует окрестность такая, что для
всех точек X
верно f(x)=g(x),
и при этом существует
8. Теорема о сжатой переменной
Д-во: Возьмем произвольное ε>0.
Возьмем
Справедливы все три утверждения:
По
определению предела имеем
9. Предел суммы, произведения, частного. 1)
Д-во Представим
f(x)
= A
+ (x),
g(x)
= B
+ (x),
где
f(x) g(x) = (A + B) + (x) + (x) A + B = const, (х) + (х) – бесконечно малая, значит
2)
Д-во
Представим f(x)
= A
+ (x),
g(x)
= B
+ (x),
где
AB = const, (х) и (х) – бесконечно малые, значит
3)
|
|
10. Предел суперпозиции.
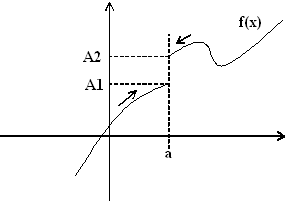
11. Бесконечные пределы и пределы на бесконечности. Односторонние пределы. Если
f(x)
A1
при х
а только при x
< a,
то
П Пределы А1 и А2 называются также односторонними пределами функции f(x) в точке х = а. Также говорят, что А – конечный предел функции f(x). 1 Первый замечательный предел S∆OCB<S∆OAB<S∆ODB 1/2sin(x)<1/2x<1/2tg(x)
|
13.
Теорема о пределе монотонной ограниченной
последовательности.
Монотонная ограниченная последовательность имеет предел. Д-во: Рассмотрим монотонную неубывающую последовательность х1 х2 х3 … хn xn+1 … Эта последовательность ограничена сверху: xn M, где М – некоторое число. Т.к. любое, ограниченное сверху, числовое множество имеет четкую верхнюю грань, то для любого >0 существует такое число N, что xN > a - , где а – некоторая верхняя грань множества. Т.к. {xn}- неубывающая последовательность, то при N > n а- < xN xn, xn > a - . Отсюда a - < xn < a + - < xn – a < или xn - a< , т.е. lim xn = a. Для остальных монотонных последовательностей доказательство аналогично.
Рассмотрим
последовательность {xn}
=
Если последовательность {xn} монотонная и ограниченная, то она имеет конечный предел. По формуле бинома Ньютона:
или, что то же самое
{xn} – возрастающая. Действительно, запишем выражение xn+1 и сравним его с выражением xn:
Докажем теперь, что при любом n ее члены не превосходят трех: xn < 3.
Итак,
последовательность
Из
неравенства
переходя
к пределу, получаем Таким образом, число е заключено между числами 2,5 и 3. Если взять большее количество членов ряда, то можно получить более точную оценку значения числа е. Можно показать, что число е иррациональное и его значение равно 2,71828… |
14. Сравнение предельного поведения функц. О-большое, о-малое. Эквивалентность. Пусть а – предельная точка множества Ч, заданы функции f,g:X→R, причем g(x)≠0 в некоторой проколотой окрестности точки а. 1.
Функция а есть о-малое от функции g
при x→a,
если
2.
Функции f
и g
эквивалентны при x→a,
если
3. Функция f есть О-большое от функции g при x→a (f ограничена по сравнению с g при x→a), если в некоторой проколотой окрестности точки а для некоторого К>0 выполнено неравенство |f(x)|≤K|g(x)|. При этом пишут а(x)=O(g(x)) при x→a.
|
|
15. Непрерывность функции. Классификация точек разрыва. Функция f(x), определенная в окрестности некоторой точки х0, называется непрерывной в точке х0, если предел функции и ее значение в этой точке равны, т.е.
Тот
же факт можно записать иначе:
Если функция f(x) определена в некоторой окрестности точки х0, но не является непрерывной в самой точке х0, то она называется разрывной функцией, а точка х0 – точкой разрыва. Функция f(x) называется непрерывной в точке х0, если для любого положительного числа >0 существует такое число >0, что для любых х, удовлетворяющих условию
верно
неравенство
Функция f(x) называется непрерывной в точке х = х0, если приращение функции в точке х0 является бесконечно малой величиной. f(x) = f(x0) + (x) где (х) – бесконечно малая при хх0. Свойства непрерывных функций. 1) Сумма, разность и произведение непрерывных в точке х0 функций – есть функция, непрерывная в точке х0. 2) Частное двух непрерывных функций
3) Суперпозиция непрерывных функций – есть непрерывная функция. Это свойство может быть записано следующим образом: Если u = f(x), v = g(x) – непрерывные функции в точке х = х0, то функция v = g(f(x)) – тоже непрерывная функция в этой точке.
Точка
разрыва а функции а называется: 1)
точкой устранимого разрыва, если
существует
16. Непрерывность суммы, произведения, частного сложной функции Пусть функции f,g:X→R непрерывны в точке а. Тогда функции fg, fg, f/g (при g(a)≠0) непрерывны в точке а. Д-во:
для fg и f/g доказательство аналогично.
|
17. Непрерывность монотонной функции. Непрерывность основных элементарных функций. Если значения монотонно возрастающей (убывающей) в промежутке X функции f(x) содержатся в промежутке Y и сплошь заполняют его (каждое значение y из Y принимается функцией хоть раз), то эта функция непрерывна в X. Д-во: Попробуем допустить, что в какой-нибудь точке x0 из X функция f(x) терпит разрыв, например, слева. Этот разрыв может быть только скачком. В этом случае существует предел f(x0-0), но он меньше значения f(x0). Так как для x< x0 будет f(x)≤f(x0-0), а для x> x0, очевидно f(x)≥f(x0), то функция не может принимать значений y, лежащих между числами f(x0-0) и f(x0), принадлежащими промежутку Y. Это противоречит условию теоремы. Значит, на деле функция f(x) разрывов не имеет. Целая и дробная рациональные функции.
18. Теорема об обращении непрерывной функции в ноль. Метод половинного деления. Первая теорема Больцано-Коши. П
Метод половинного деления: Пусть
функция а непрерывна на отрезке [a,b]
и f(a)f(b)<0.
По теореме Больцано-Коши на (a,b)
лежит корень (может не единственный)
уравнения f(x)=0.
Разделим [a,b]
пополам. Если f((a+b)/2)=0,
то (a+b)/2
– корень. Иначе, обозначим через
[a1,b1]
тот из отрезков [a,(a+b)/2]
и [(a+b)/2,b],
на концах которого функция f
принимает значения разных знаков. По
построению b1
-a1=(b-a)/2.
К промежутку [a1,b1]
применим описанный процесс деления
пополам. Если на некотором этапе
f((an+bn)/2)=0,
то (an+bn)/2
– корень. В противном случае процесс
деления пополам продолжается до тех
пор, пока не будет выполнено неравенство
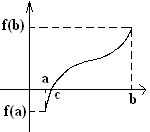
19. Теорема о промежуточном значении непрерывной функции. Вторая теорема Больцано – Коши:
|
20. Теорема Вейерштрасса
21. Дифференцируемость функции. Производная. Касательная к графику функции. Функция дифференцируема в точке x0, если существует A принадлежащее R такое, что f(x)=f(x0)+A(x-x0)+o(x-x0). Функция A(x-x0) называется дифференциалом функции f и обозначается d’x0 f. По определению функция f дифференцируема в x0, если она отличается от некоторого многочлена первой степени f(x0)+A(x-x0) на бесконечно малую величину высшего порядка малости, чем x- x0 при x→ x0.
Если f дифференцируема в точке x0, т.е. представима в виде f(x)=f(x0)+A(x-x0)+o(x-x0), то существует f’(x0)=A Д-во: Т.к. существует предел
то существует производная f’(x0) и она равна А Прямая f= f(x0)+A(x-x0) называется касательной к графику функции f в точке x0, если f(x)-y=f(x)-(f(x0)+A(x- x0))=o(x-x0) Касательная к графику функции f существует только тогда, когда f дифференцируема в точке x0. И т. К. функция дифференцируема, то уравнение касательной имеет вид y=f(x0)+f’(x0)(x-x0) Производная f’(x0) есть угловой коэффициент касательной к графику функции f в точке x0. Поэтому f’(x0)=tgα, где α – угол наклона касательной к Ox. Если функция f дифференцируема в точке x0, то f непрерывна в точке x0. Д-во:
|
|
22. Дифференцируемость суперпозиции функций и обратной функции. Пусть f:X→Y, g:X→R. Если функции f и g дифференцируемы в точках x0X и y0=f(x0)Y соответственно, то их суперпозиция g o f:X→К дифференцируема в точке x0 и (g o f)'(x0)=g'(f(x0))f '(x0). Д-во: По условию g(y)=g(y0)+g’(y0)(y-y0)+o(y-y0). Рассмотрим функцию :Y→R, (y)=(o(y-y0)/(y-y0)), если y≠y0 и (y)=0. Тогда
Заменяя в последнем равенстве y=f(x), y0=f(x0), y-y0=f(x)-f(x0)=f’(x0)(x-x0)+o(x-x0), получим: g(f(x))=g(f(x0))+g’(f(x0))f’(x0)(x-x0)+α(x), где α(x)=g’(f(x0))o(x-x0)+(f(x))(f(x)-f(x0)). Остается показать, что α(x)= o(x-x0). Так как
Итак, g(f(x))=g(f(x0))+g’(f(x0))f’(x0)(x-x0)+o(x-x0) или, что то же самое, (g o f)(x)=(g o f)(x0)+ g’(f(x0))f’(x0)(x-x0)+o(x-x0) По определению дифференцирования суперпозиция g o f дифференцируема в точке x0.
|
23. Теорема Ферма, Ролля. Теорема Ферма:
Следствие: Если в точке x0, предельной слева и справа для множества Х, функция f достигает максимума (минимума) и существует f’(x0), то f’(x0)=0. Теорема Ролля: Пусть функция f:[a,b]→R непрерывна на [a,b] и дифференцируема в любой точке из [a,b]. Если f(a)=f(b), то существует точка x0(a,b) такая, что f’(x0)=0.
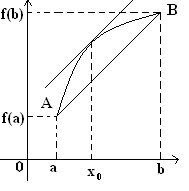
24. Теорема Коши, Лагранжа Теорема Коши:
|
Теорема Лагранжа: Пусть функция f:[a,b]→R непрерывна на [a,b] и дифференцируема в любой точке из [a,b]. Тогда существует точка x0(a,b) такая, что f(b)-f(a)=f’(x0)(b-a) (Формула Лагранжа).
Теорема Лагранжа имеет простой геометрический смысл. Очевидно, что (
24. Теорема Лопиталя.
|
|
26. Формула Тейлора с остаточным членом в форме Пеано.
|
27. Формула Тейлора с остаточным членом в форме Лагранжа.
|
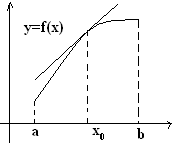
28. Условия монотонности и постоянства функции. Функция f:[a,b]R непрерывна на [a,b] и дифференцируема во всех точках (a,b). Теорема. 1) Функция f не убывает (не возрастает, постоянна) на [a,b] f’≥0(≤0,=0) на (a,b); 2) Если f’>0(<0) на (a,b), то f возрастает (убывает) на [a,b].
29. Экстремум функции. Необходимые и достаточные условия. Пусть f:XR, x0X предельная точка множества X. Если x0 предельная справа (на не слева) или x0 предельная слева (но не справа) иди f’(x0)=0, или f’(x0) не существует, то x0 называется критической точкой функции f. По следствию из теоремы Ферма функция может иметь экстремум только в критических точках. Этот факт называют необходимым условием экстремума. Достаточные условия существования экстремума. Теорема. Пусть
функция f
непрерывна в точке x0,
для некоторого ε>0 Kε(x0)
и существует f’
в
1. Если f’>0 на (x0-ε,x0) и f’<0 на (x0,x0+ε), то x0-точка максимума. 2. Если f’<0 на (x0-ε,x0) и f’>0 на (x0,x0+ε), то x0- точка минимума. 3. Если f’>0 (<0) на (x0-ε,x0)(x0,x0+ε), то в точке x0 экстремума нет. Д-во: 1. По теореме о монотонности f возрастает на (x0-ε,x0) и убывает (x0,x0+ε), a потому для x
2. Аналогично 1-му. 3. По теореме о монотонности f возрастает (убывает) на (x0-ε,x0+ε), а пототму в точке x0 экстремума нет. Критическая точка x0 функции f называется стационарной, если f’(x0)=0. |
|
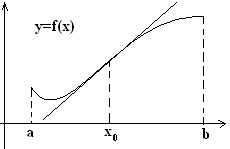
30. Выпуклость, вогнутость. Точки перегиба. Пусть
f:XR
дифференцируема в точке x0X.
Будем говорить, что функция f
выпукла вниз (вверх) в точке x0,
если существует ε>0 такое, что для
любого
Геометрически выпуклость вверх(вниз) означает, что в некоторой проколотой окрестности x0 график лежит выше (ниже) касательной к графику в точке x0.
Е
Точки, при переходе через которые характер выпуклости функции f меняются, называются точками перегиба функции. Пусть x0 точка перегиба функции f. Если существует f”(x0), то f”(x0)=0. Д-во: Допустим, что f”(x0)>0(<). Тогда по теореме о выпуклости функция выпукла вниз (вверх) в точке x0, что противоречит условию. Следовательно f”(x0)=0. Если при переходе через “подозрительную” точку x0 вторая производная меняет знак, то x0-точка перегиба. В противном случае перегиба нет. |
31. Асимптоты графика функции.
32. Многочлены. Основная теорема высшей алгебры. Теоремы Безу. Корни простые и кратные. Функция
вида f(x) Основная теорема алгебры Всякая целая рациональная функция f(x) имеет, по крайней мере, один корень, действительный или комплексный. Теорема Безу. При делении многочлена f(x) на разность x – a получается остаток, равный f(a). Д-во: При делении многочлена f(x) на разность x – a частным будет многочлен f1(x) степени на единицу меньшей, чем f(x), а остатком – постоянное число R.
Переходя к пределу при х a, получаем f(a) = R. Если, а – корень многочлена, т.е. f(a) = 0, то многочлен f(x) делится на (х – а) без остатка. Если уравнение имеет вид Р(х) = 0, где Р(х) – многочлен степени n, то это уравнение называется алгебраическим уравнением степени n.
|
33. Многочлены с вещественными коэффициентами. Разложение на множители. Всякий многочлен n – ой степени разлагается на n линейных множителей вида (x – a) и множитель, равный коэффициенту при xn. Если два многочлена тождественно равны друг другу, то коэффициенты одного многочлена равны соответствующим коэффициентам другого. Если среди корней многочлена встречаются кратные корни, то разложение на множители имеет вид:
ki - кратность соответствующего корня. Отсюда следует, что любой многочлен n – ой степени имеет ровно n корней (действительных или комплексных).
|

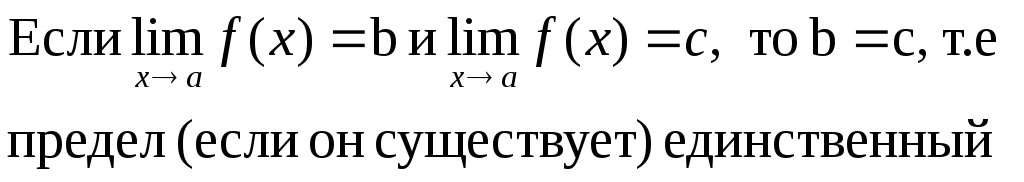


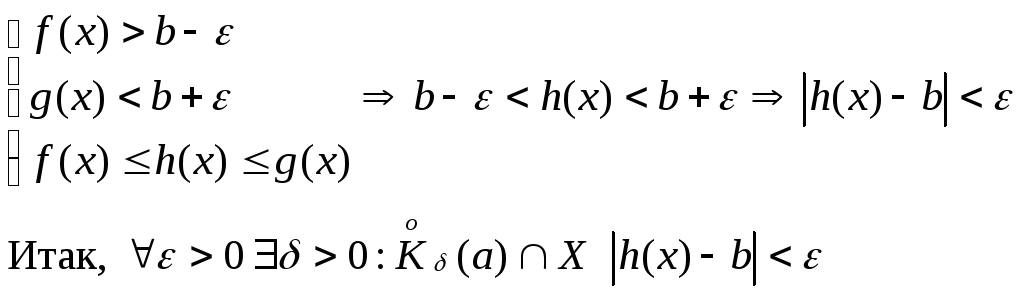
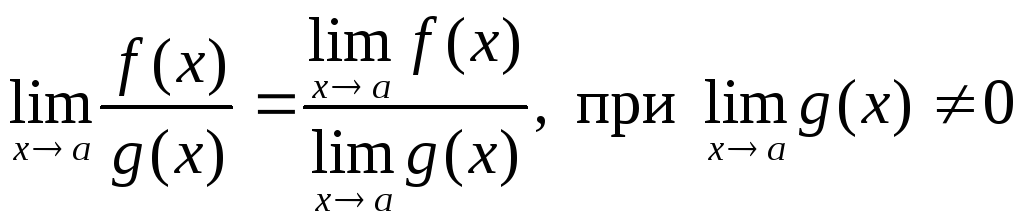
 риведенное
выше определение относится к случаю,
когда функция f(x)
не определена в самой точке х = а, но
определена в некоторой сколь угодно
малой окрестности этой точки.
риведенное
выше определение относится к случаю,
когда функция f(x)
не определена в самой точке х = а, но
определена в некоторой сколь угодно
малой окрестности этой точки. 2.
Предел
2.
Предел

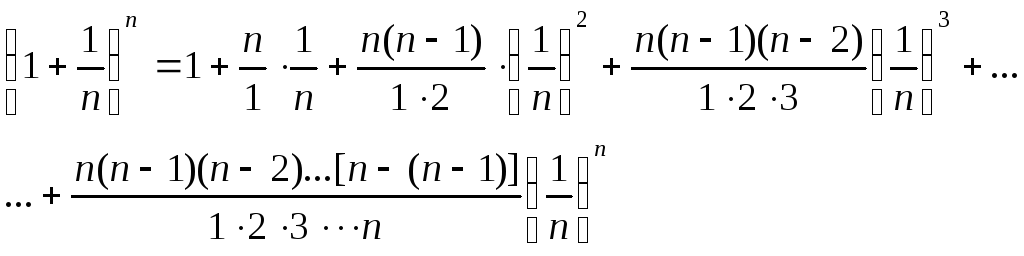
 Каждое
слагаемое в выражении xn+1
больше соответствующего значения xn,
и, кроме того, у xn+1
добавляется еще одно положительное
слагаемое. Таким образом, последовательность
{xn}
возрастающая.
Каждое
слагаемое в выражении xn+1
больше соответствующего значения xn,
и, кроме того, у xn+1
добавляется еще одно положительное
слагаемое. Таким образом, последовательность
{xn}
возрастающая.